金融风险分析结果：VaR 多尺度估值与置信水平的相对偏差

本节利用Wav Lab8.5工具箱编写程序，执行估值算法步骤1～5，计算样本密度的小波阈值估计量；执行算法步骤5～6，计算估值精度和不同置信水平的VaR 多尺度估值及相对偏差，结果分别见图4.2、表4.1和表4.2。

表4.1　MSE的估计结果

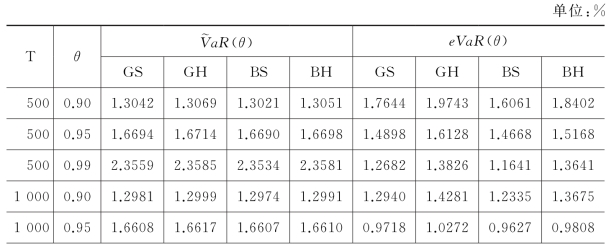
表4.2　风险价值的多尺度估值及其相对偏差

续表

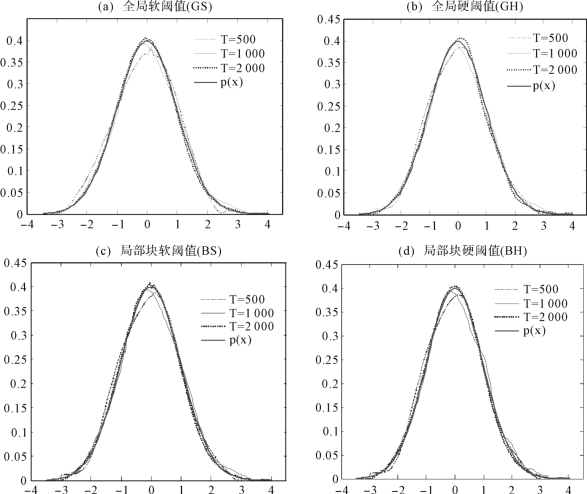
图4.2　基于不同样本容量和阈值规则的密度估计量与真实密度

由图4.2可见：(www.xing528.com)

①密度估计量(x)随样本容量增大而更接近真实密度p(x)，这表明四种非线性阈值方法有较好的估计效果；

②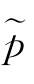(x)的优劣顺序为BS＞GH＞BH＞GS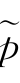，(x)左尾估计顺序为BS＞GH＞BH＞GS，(x)右尾估计顺序为BS＞GH＞BH＞GS，进而四种阈值规则对密度局部特征的量化存在一定的差异.表4.1中MSE(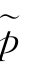)的变化趋势证实基于BS规则的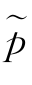(x)是密度的最优估计量。

表4.2中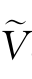aR(ϑ)及eVaR(ϑ)的趋势表明：

①当ϑ 不变时，随着样本容量增大eVaR 变小，这显示出VaR 的估值精度显著得到改进；

②当样本容量不变时，ϑ 增大，eVaR 变小，VaR 估值精度明显得到提高；

③四种阈值规则的VaR 排序为BS＞BH＞GS＞GH，进而说明小波局部块软阈值(BS)方法的自适应能力最强，因此在VaR 的多尺度模型应是首选的阈值规则。

总体而言：

1.从以上仿真分析看来，基于BS准则的密度估计量(x)更有助于改进VaR(ϑ)的计算精度，在不同置信水平下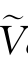aR(ϑ)随样本容量T增大，VaR(ϑ)的估计偏差越来越小而且其收敛速度加快，这证实了模型(4.7)在理论上的正确性。

2.对金融机构来说，准确的估计VaR 能够更加合理地利用资金，低估的VaR 会给金融机构带来很大的风险，但高估的VaR 会使得资金不能充分地利用，因此金融机构都不愿意接受高估和低估的VaR 值，因而VaR 的多尺度估值模型在风险管理中具有重要的应用潜力。