金融风险价值量化分析-密度阈值估计量

小波分析中的多尺度算法为密度函数空间的分解提供了一套直观的嵌入式层次思维(Vidakovic，1999)。若φ(x)、ψ(x)分别为L 2(R)正交多尺度分解的尺度函数和小波函数，对适当的初始尺度J 0，任何密度函数p(x)的小波展开为

其中

ψj，k(x)＝2j/2ψ(2j x－k)，I j＝{1，2，…，2j－1}，j≥J 0。假设{x n}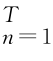抽取于p(x)，则系数的样本估计为

由此得到(4.1)式的样本估计为

对有限样本而言，式(4.3)中J 0≤j≤J max(J 0＝0，J max＝2 log(T))，J max为最大分解尺度.倘若采用尺度截断的办法对p(x)进行小波线性估计，那么根据式(4.2)计算系数存在两个问题：(1)如何选取截断尺度j使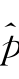(x)能够体现p(x)的全局趋势特征和局部细节特征；(2)如何选择阈值对系数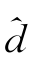jk进行处理，使得由式(4.2)计算出的小波系数少受样本携带的异常新息(innovation)的影响。Donoho等(1996)认为线性阈值规则(L)和非线性阈值规则(N)适于对系数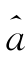J 0，k和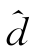j，k的修正。由于L 规则(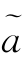J 0，k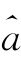＝J 0，k和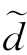j，k＝0)保留了密度函数的趋势而忽略了细节，因此可以采用N 规则中的硬阈值(H)和软阈值(S)方法调整小波系数

其中非线性阈值参数σT 对同一尺度上的经验小波系数按照同一标准处理。对具有非平稳性等特征的样本而言，这可能导致过度扭曲原样本的复杂特征。这里我们结合变点识别技术，选用小波模极大值线方法(傅强等，2007)，识别各尺度上子列的可能变点，接着利用局部分块自适应阈值规则(Chicken and Cai，2005)，最后给出概率密度的四种阈值估计量的计算公式。具体而言分为如下三步：

1.(L－1)个变点将尺度j 的小波系数分割成L 个子块，对应小波方差为(www.xing528.com)

2.子块阈值参数取为σ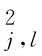，小波系数的块阈值修正为

3.密度函数p(x)的小波阈值估计量为

其中μ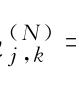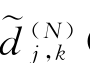＝(N∈{GS，GH，BS，BH})分别表示全局软阈值规则、全局硬阈值规则、局部块软阈值规则和局部块硬阈值规则对应的小波系数。

由此可见N 规则在高频金融数据分析中能刻自适应地画收益率密度的局部特征，进而本文将式(4.6)用于资产市场风险度量，主要研究三个问题：(1)根据VaR 的定义提出VaR 的多尺度估值模型；(2)四种阈值准则对应于VaR 的估值误差及其收敛性的影响分析；(3)基于不同样本容量的仿真实验证实以上分析结论。

令{x i} 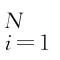的累积概率密度为P(x)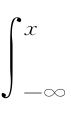＝p(r)dr。假设损失概率为ϑ，则风险价值(VaR)为VaR(ϑ)＝i x n∈f R{x|P(x)＝ϑ}。结合式(4.6)，我们得到VaR(ϑ)的多尺度估值模型为：