多尺度模型结果-金融风险分析

通过表3.1的检验结果设定具体的多尺度模型，本节分析上证指数收益率序列在投资期限16～32天、8～16天、4～8天、2～4天、1～2天等的波动特征。

由表3.1的分析可知：运用LA(8)小波的MODWT 变换后，上证指数在不同时间尺度上的收益率序列在5%置信水平下平稳，还具有尖峰、厚尾等分布特征且统计检验的结果显著，因此多尺度模型拟设定为

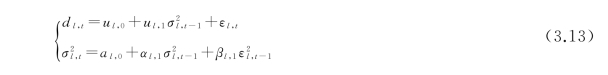
其中εt，l ＝z t，lσt，l，z t，l ～i.i。D(0，1)，a l，0 ＞0，0＜αl，1 ＋βl，1 ＜1。式(3.13)中波动方程也满足众多文献设定的GARCH(1，1)模型(张世英和樊智，2004)。其中无条件方差σ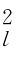＝a l，0/(αl，1＋βl，1)表示资产收益率在尺度l上的均衡风险，波动持续性参数p l＝αl，1＋βl，1量化了投资者对不同时间尺度上的已实现收益率风险的记忆程度。

为了比较不同新息分布的多尺度模型的功效以及最佳地捕捉到上证综合指数收益率在不同时间尺度上的波动特征，z t，l的分布设定为标准正态分布(i.i.N)和学生分布(i.i.T)，则对数似然函数分别为

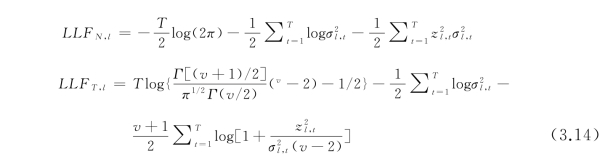
我们利用软件Matlab2010 和S-plus2000 分别对第3.4 节的计算方法(OM 算法)和BHHH 算法编程，实现多尺度模型(3.13)的参数估计，结果见表3.2和3.3，其中(*)为参数估值的偏差。

从表3.2可见：

1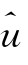l，0值都很小，其中D1的值为正而其他尺度的值都为负，这表明不同时间尺度的投资者对市场无风险收益都持有消极的态度；

2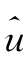l，1在2～4之间因时间尺度而变化的趋势表明投资者对规避市场风险的情绪因资产交易的时间尺度而变化，这与Poterba and Summers(1986)的结论一致；

3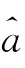l，0值也很小，表明不同投资期限上的投资者对确定性风险的估计都趋于乐观，固定时间尺度上的多头或空头交易行为都不可能引起市场的大幅波动；(www.xing528.com)

4.R t的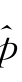l 为0.9922，S1的值为0.9562，D1～D5的值近似为1.0000，表明不同时间尺度的投资者对资产收益率风险的记忆性不同；

5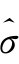l×10－4 分别为0.0622、0.0021、0.0020、0.0052、0.0130、0.0321 和0.1755，表明投资者对均衡风险的量化值因交易周期而变化。

表3.2　标准正态分布的模型参数估计结果

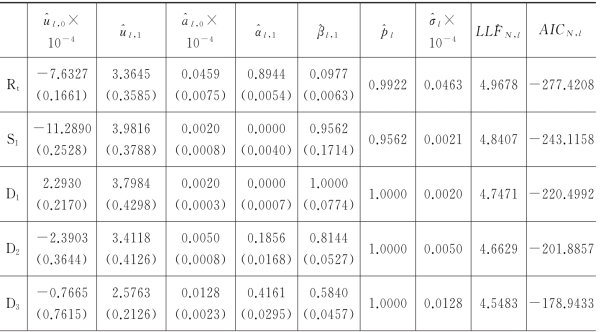
续表

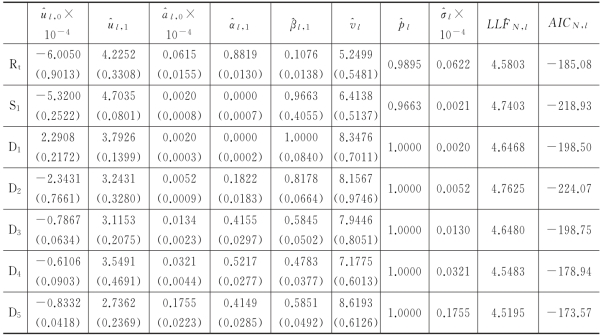
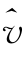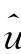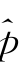表3.3显示，新息分布函数的自由度参数l 均大于3，说明各尺度上新息分布的尖峰特征明显，这验证了表3.1中的统计结果.与表3.2中不同的是多尺度模型对应其他参数的估值差异较为明显，特别是l，1l 和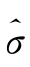l×10－4的变化更能较为合理地度量上证指数收益率在不同时间尺度上的波动幅度，因而新息分布设定为标准学生氏分布比标准正态分布更具有优势.此外极大似然函数随尺度变化有减小趋势，说明多尺度模型捕捉资产价格信息也具有尺度差异，这与模型参数的估值算法有关，因此多尺度模型的极大似然函数作为评价模型及算法的优良性指标。

根据以上两个多尺度模型捕捉到上证指数收益率波动的多尺度特征，我们从行为金融学的角度将其解释为，投资行为的异质性是这种特征存在的根本原因，也即投资者按不同的交易周期买卖资产的行为铸造了我国资本市场的这种波动特征。一方面，当市场突然受到某个利好消息的冲击时，部分机构投资者提前得知利好消息后迅速增仓，随着利好信息的进一步扩散，其他类型的投资者也纷纷参与资产买卖，由此迫使固定交易周期的交易者改变资产交易周期，进而也参与临时的短期交易；另一方面，当市场受到利空消息冲击时市场行情上涨乏力，这时前期做多的投资者迅速获利出局，众多投资者迫于市场持续下跌而改变自己的投资周期，以便减小持仓风险，因此顺风抛售资产使得市场步入熊市行情。

表3.3　标准学生分布的模型参数估计结果

由此可见，资产价格的波动特征体现了投资者的异质性及其交易周期随着市场行情的不断修正，同时伴随着羊群行为时有发生，利用多尺度模型研究资产的波动特征是一种有效的分析工具，这对不同时间尺度下资产的组合风险管理和最优化配置也具有独特的决策优势。