金融风险价值量化分析中的参数估计算法及其改进

极大似然估计(MLE)是计量经济学模型参数估值的经典方法(张世英和樊智，2004)。由于在不同时间尺度上MLE 方法对小波子列拟合多尺度模型时，模型结构的复杂性导致BHHH 算法的收敛性和稳定较差，因此通过分析多尺度似然函数的取得极值的必要条件，尝试运用Marquardt-Levenberg算法改进BHHH 算法的参数迭代步长，最后给出多尺度模型参数估值的OM算法。

假设资产收益率时序的MODWT 变换是完全分解的，小波子列中不含有近似趋势成分。若z l，t的分布函数为f(z l，t)，z l，t＝(d l，t－m l，t)/σl，t，r＝{r t}|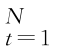的多尺度分解为D l ＝{d l，t}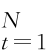，l＝1，…，J 且最大分解尺度J＝[log2N]，模型共含有np＝3(p l＋1)＋2q l＋8个参数，则对数似然函数为

由式(3.6)可知：当LL(θ，X)取最大值时，参数θ 等同于当LL(θ，D l)最大时尺度分量参数的取值，因此进一步讨论多尺度模型参数在极大似然估计框架下的一般条件。

定理3.1:如果LL(θ，D l)关于θ 具有足够的光滑度且至少存在两阶混合偏导数，那么极大似然估计量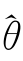∈Θ，其中

证明:由于L(θ，X)及其分量LL(θ，D l)关于参数θ 足够光滑且两阶混合偏导数存在，因此在极大似然估计点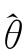 处，似然函数LL(θ，D l)的泰勒展开式为

依据连续函数取得局部极值的必要条件可得

在该条件下，(3.7)式分两种情况讨论：

因此满足式(3.6)、(3.8)和(Ⅱ)的似然函数分量LL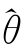，D l)取极大值时。参数取值空间为

注3.1：定理3.1提供了一种基本的数值优化条件。对具体的多尺度模型而言，参数附加的约束条件使集合Θ 变得更小(不妨记为Θ′)。利用BH HH算法对多尺度模型参数估计的数值优化思想为：在给定初值点θ(0)和目标点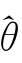寻找M 个点，建立一条最优化的参数路径P：θ(0)→θ(1)→θ(2)→…→θ(M－1)→θ(M)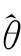＝，使得LL(θ，D l)逐渐增大到最大值，其一阶导数∂L(θ，X)/∂θ 在P上逐渐逼近零(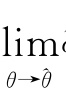∂L(θ，X)/∂θ＝0)，同时二阶导数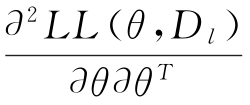＜0。对任意i∈{0，1，…，M}，若λi 是第i点的最佳搜索步长，则参数迭代式为θ(i＋1)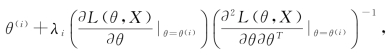＝因而BHH H 算法表明在余空间Θ′＝R n－Θ 内某初值点θ(0)规划一条含M 个节点的通往最优点 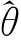的路径P。因此，约束集上的离散化迭代思想为：通过有限次迭代确保似然函数局部极大，对不连续的点可以单独计算似然函数，然后与局部极值点的大小比较即可得到优化的极值点。

定理3.2:对任意θ(0)∈Θ′及解析函数f(θ)，G(θ)＝▽f(θ)，H(θ)＝▽2f(θ)，I 表示单位矩阵；令θ(i)＝θ(i－1)－G(θ(i－1))H－1(θ(i－1))(i＝1，2，…，M)，当i＞M 时θ(i)＝θ(M)，则：

(Ⅰ)如果H(θ(0))＜0，那么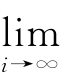θ(i)＝θ(M)且θ(M)∈Θ′为函数f(θ)的一个极大值点；

(Ⅱ)如果H(θ(0))≥0，记λ＝max{λn‖H(θ(0))－λn I|＝0，n＝0，1，…，np}且H(θ(0))＝▽2 f(θ(0))－λI，那么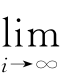θ(i)＝θ(M)且θ(M)∈Θ′为函数f(θ)的一个极大值点.(www.xing528.com)

证明:(Ⅰ)假设θ(i)的极限为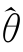，只需证明两点：其一 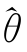恰好等于θ(M)；其二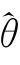∈Θ。

将f(θ)类似于式(3.7)展开，对i＝1，2，…，M，▽θ(i)＝θ(i)－θ(i－1)，可得

由式(3.9)得G(θ(i－1))＝▽f(θ(i－1))，H(θ(i－1))＝▽2 f(θ(i－1))，因而▽G(θ(i))＝▽θ(i)H(θ(i－1))，并令G(θ(i))＝0，则

由式(3.10)，易见{θ(i)}为单调序列，而且其极限满足G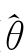)H－1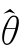)＝0。根据θ(i)的定义，得到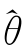＝θ(M)。再由定理3.1，得到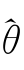∈Θ。

(Ⅱ)类似于(Ⅰ)，按照条件只需把初始点θ(0)修改为满足条件的θ(1)，证毕。

注3.2:式(3.10)的完整形式为θ(i)＝θ(i－1)＋G(θ(i))H－1(θ(i－1))－G(θ(i－1))H－1(θ(i－1))。由于在参数迭代过程中：假设下一个点是极大值点并令G(θ(i))＝0；令G(θ(i))＝(λ(i)＋1)G(θ(i－1))，式(3.10)为BH HH 算法的迭代公式θ(i)＝θ(i－1)＋λ(i)G(θ(i－1))H－1(θ(i－1))。BH H H 算法应用于多尺度模型的极大似然函数的优化估值，完全可以达到局部优化的目的，但存在两点不足：(1)最优结果易受初值影响，使得估计值为局部极大值点；(2)对确定方向上的最佳步长λi 的取值表现得十分冗余，使得搜索步数增加，在局部极大值点振荡。张世英等[8]建议采用遗传禁忌搜索算法改进增广GARCH 类模型的参数估值的BHHH 算法。但该算法的计算量大且耗时过久。因此我们通过修正步长参数，改进BHH H 算法的估计效果，然后根据定理3.2给出多尺度模型基于有限样本的参数迭代原理。

定理3.3:假设资产收益率时序为X ＝{x t}|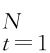，其多尺度分析为D l＝{d l，t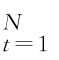(l＝1，…，J)，对任意θ(0)∈R np 及LL(θ，D l)，那么必然存在{θ(i)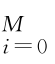，使得

证明:结合式(3.6)及定理3.1和定理3.2，结论显然成立。

定理3.3表明总可以通过有限样本以离散化的迭代方式完成多尺度模型的参数估计。因此，参数估值步骤设定如下：么停止计算并输出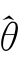＝θ(i)和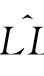l，i及最大迭代步数M ＝1＋i；否则转步骤3。

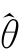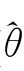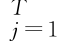注3.3：类似Bootstrap检验参数估值稳定性.也即，仿真T 次由 确定的多尺度模型，利用步骤1～4重新估计参数值{j}，则均值类似于Bollerslev等(1992)讨论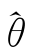 的渐近分布特征。值得注意的是本章对参数约束问题的理论分析是另文所要报道的结果。为了便于比较结果，步骤1～4简记为“OM 算法”。

注3.4:实证分析表明标准正态分布、T 分布、GED 分布等密度函数可用于拟合资产收益率的真实分布密度f(z l，t)，但这些分布有时候并不能很好地拟合某些高频金融数据的分布。