金融风险价值量化分析：多尺度模型及参数估计问题

为了从多时间尺度的视角研究资产收益率的波动特征，本节将MODWT多尺度分解理论融入GARCH 模型和增广FIGARCH-M 模型，分别定义多尺度GARCH 模型(记为：MRA-GARCH)和多尺度增广FIGARCH-M 模型(记为：MRA-AFIGARCH-M)。

定义3.1:MRA-GARCH 若r＝{r t}|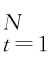的MODWT 多尺度分析为D l＝{d l，t}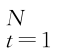，l＝1，…，J I.l，t－1表示在尺度l上t－1时刻的信息集，则：

其中，p l≥0，q l≥0，a 0，l＞0，αt，l≥0(i＝1，2，…，q l)，βj，l≥0(j＝1，2，…，p l)。

定义3.1表明：①当z l，t－1具有不同形式的分布函数时，式(4)对应于不同的多尺度模型。譬如，“i.i.d”取为标准正态分布(N)，学生分布(T)等；②当价格新息在不同时间尺度上的投资者之间的传递速度存在显著的差异和非对称性时，式(3.4)中f(.)，g(.)可取不同的解析式。

由此可见定义3.1也包容了多种具体形式的多尺度GARCH 模型。伴随着GARCH 理论的不断向前发展，该模型形式仍然具有局限性，下面借鉴文献(Duan，1997；张世英和樊智，2004；许启发等，2007)，对MRA-GARCH 模型做进一步拓展。

定义3.2:MRA-AFIGARCH-M 若r＝{r t}|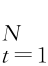的MODWT 多尺度分析为D l＝{d l，t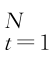(l＝1，…，J)，I l，t－1表示尺度l 内t－1时刻的新息集，则模型结构设定为：(www.xing528.com)

其中g(|z l，t－j－c l|，δl)＝(|z l，t－j－c l|δl －1)/δl，g(max(0，c lz l，t－j)，δl)＝(maxδl(0，c l－z l，t－j)－1)/δl。

定义3.2表明MRA-AFIGARCH-M 是一个综合性极强的金融计量模型。该模型在不同尺度上能一次性地捕捉到收益率的记忆性、分形性、持续性等波动特征，据此还可以推测市场的微观结构特征以及量化不同交易周期的投资行为的异质性。

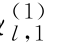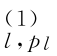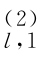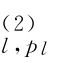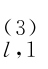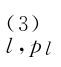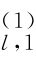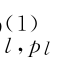定义3.2的模型参数记为θl＝[μl，k l，λl，αl，δl，c l，βl]，其中均值方程含有8个参数，波动方程含有3(p l＋1)＋2q l 个参数，k l 为记忆性参数，λl 和δl为示性参数，c l 为阈值参数，μl＝[μl，0，μl，1，μl，2，μl，3，μl，4]，αl＝[α，α，…，α，α，…，α，α，…，α]，βl＝[β，…，β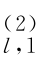，β，…，β]。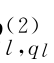

接下来我们考虑这两类多尺度模型的参数估计问题。