我们已经发现投资组合多分辨率边际风险价值的重要特征，下面根据命题2.2计算表2.3所列出的16个投资组合的多分辨率边际风险价值。表2.5中给出等权重组合X 0 和均匀分布权重组合X 15 在95%置信水平下的MRAMVaR，图2.2展示了基组合(X 1～X 14)在95%置信水平下的MRAMVaR。
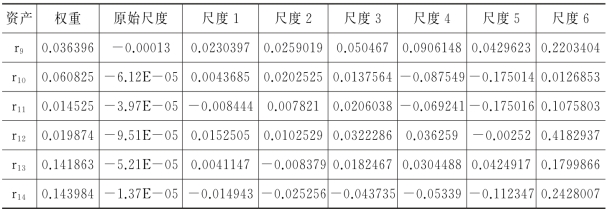
表2.5显示对单个资产分别增加投资1元人民币，则在95%的置信水平下投资组合的风险价值变化(上升或者下降)幅度将非常小。具体而言，在等权重组合X 0中，若对r 1增加1元投资额，则在95%的置信水平下投资组合X 0的风险价值在2～4天内减少0.0314元，在4～8天内减少0.0341元，在8～16天内减少0.0428元，在16～32天内减少0.0333元，在32～64天内减少0.0443元，在64～128天内减少0.1007元，这体现了在恰当的时间尺度上可以调整该资产的比重，从而有助于降低组合风险价值。均匀分布权重投资组合也有相似的解读含义。
表2.5 投资组合x的多分辨率边际风险价值(MRAMVaR)
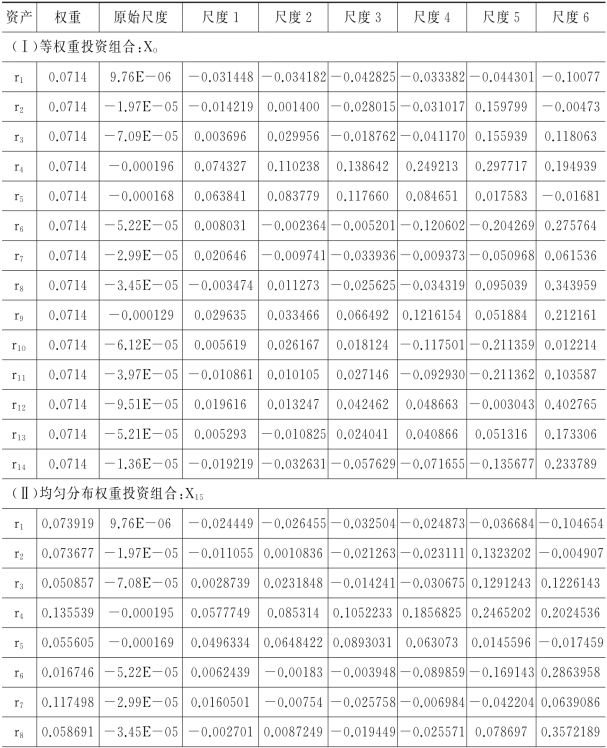
续表
(www.xing528.com)
注2.2：表中(1～7)列的单元格中数据大小表示组合的VaR 变动幅度，正号表示增加风险价值，负号表示减少风险价值。
从图2.2可知，(a)～(e)、(g)、(j)、(m)等八种基组合的边际风险价值随着尺度有一致的变动趋势，而另外6种基组合的边际风险价值有相反的变动趋势。这意味着MRA-MVaR 可以作为优化投资组合的一个约束条件，即根据单个资产的MRA-MvaR在不同投资时限上的变化规律调整原投资组合的权重，以使投资组合风险价值在不同尺度上得到最小化。目前国内已有学者提出了多分辨率投资组合优化模型(蒋翠侠，2007)，如果把MRA-MVaR作为该模型求解的约束条件，那么求解出来的组合必将更符合实际投资活动的需要。
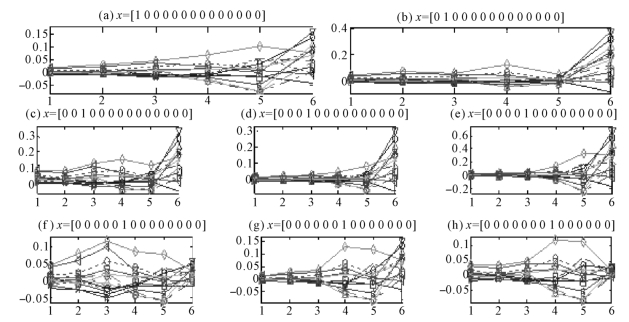
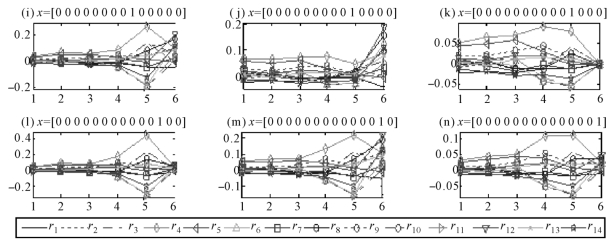
图2.2 基组合的多分辨率边际风险价值
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
