金融风险价值量化分析：小波变换与方差估计

若父小波φ(t)表示信号的低频(趋势)构筑块，母小波ψ(t)表示信号的高频(细节)构筑块，则信号f(t)的小波分解的逼近形式为

其中J 为分解的最大尺度，L j 为每个尺度上的小波函数个数，φj，Lj(t)和ψj，Lj(t)分别为尺度函数和小波函数，也即

A J 表示尺度系数、d j(j＝1，2，…，J)表示细节系数，也即

由于φj，Lj(t)和ψj，Lj(t)是对φ 和ψ 进行二进制尺度变换和位置变换的结果，因此式(2.9)表明在变换尺度参数为τj＝2j，位置参数为t＝2j L j 处，随着j 增大时φj，Lj(t)和ψj，Lj(t)的图像都会变窄。由此可见小波变换有很多优点，譬如应用到时间序列信号的局部特征检测。

Percival and Walden(2000)给出了时间序列的离散小波变换及其向量表示方法。令X＝{x t，t＝0，1，2，…，N－1}，其中N ＝C×2J，C 为常数，J 为正整数。X 的J 级离散小波变换(DWT)是W ＝w X 给出的正交变换，其中W 是由DWT 系数构成的N 维向量，w 是一个N×N 维实值矩阵(若N ＝2M，M ＝J，则得到完全的DWT)。向量W 和矩阵w 的结构分别为

其中W j＝w j X，V J＝v J X，j＝1，2，…，J，W j 是一个L j＝N/2j 维的与尺度τj＝2j 上变化相关的小波系数向量；w j 是一个L j×N 维矩阵；V J 是一个N J 维与尺度τJ＝2J 上变化相关的近似尺度系数向量；v J 是一个N J×N维矩阵，于是序列X 多尺度分解

式(2.12)是式(2.8)的一个离散表示，意味着X 分解为J＋1个N 维向量D j＝w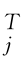W j(j＝1，…，J)和A J＝vV J。A J 为对应于最大尺度τJ 的J 级近似序列，D j 为对应于尺度τj 的j 级细节序列。本章实证中D j 叫作小波收益率序列。(www.xing528.com)

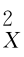记{X t表示资产收益率序列，σ 表示其方差，尺度τj＝2j 的小波方差为v(τj)，Percival and Walden(2000)证明了样本方差可以分解为不同时间尺度上小波方差之和，分量大小表明不同尺度的小波方差对样本方差的贡献大小，因此

记n′j＝[2－jn]为不超过2－jn 的最大整数(n 为样本容量大小)，表示尺度τj 上离散小波变换(DWT)的系数个数表示尺度τj上的边界系数个数，L 为滤子宽度。假定n′j＞L′j，则小波方差的无偏估计为

Percival and Walden(2000)表明DWT 变换去掉了原序列的互相关性，非小波边界系数d j 是零均值的高斯白噪声。如果n′j＞L′j，{X t}，{Y t}在尺度τj上的小波协方差为

Percival and Walden(2000)指出{X t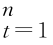的DWT 方差和协方差的估计量是有偏估计，最大重复小波变换(MODWT)是一种平稳小波变换，{X t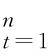基于MODWT 的小波方差的无偏估计量表示为

其中j，t 是在尺度τj 和时间t处的MODWT 小波系数，M j ＝n－L j ＋1，L j＝(2j－1)(L－1)＋1为尺度τj 处MODWT 滤子宽度。由于在任意尺度τj 处n 个MODWT 小波系数中保留边界系数会导致小波协方差的有偏估计，因此删除(L j－1)个边界系数后的小波系数可用于小波协方差的无偏估计，于是{X t}，{Y t}的MODWT 协方差的估计量为