金融风险价值量化分析中的小波分析方法

依据前面的文献述评，本节凝练出本书主体部分待研究的问题：其一是相关的国外文献趋势特征(图1.4)以及评论；其二是确立选题研究的六个突破点。

根据图1.4 可知，Copula-MCMC、Copula-MCMC-VaR、Copula-Wavelet和Wavelet-GARCH-VaR 等的组合研究都具有新意(由于国内缺少这方面的组合式方法及应用，极少文献不构成明显的趋势特征，因此这里没有给出国内文献的统计图)。从2002年开始以来，组合文献逐年缓慢增长，趋势表明小波分析、Copula理论与GARCH 等金融计量模型的融合是一种实用的金融风险量化分析的新方法。

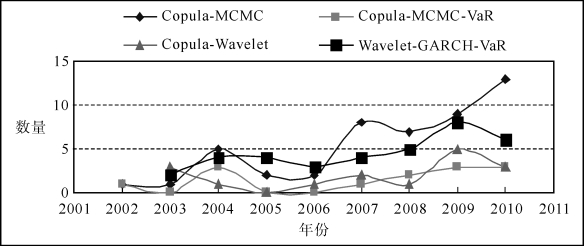
图1.4　核心文献趋势(www.xing528.com)

现阶段小波分析方法的金融应用研究存在两点不足：(1)小波分析和金融计量模型的融合度不够紧密，有必要将两者的结合上升到理论层面的探讨，进而拓展方法与模型的研究深度；(2)在小波分析结合计量模型的实证分析中，对实证结果的解释局限于模仿常规计量分析的方式，因而有待以多尺度的视角去认识实证结果所蕴含的金融现象内在的演变机制。为此本书第一部分引入小波分析方法并研究风险价值的特征与度量。依据现状我们设立四个问题并进行研究：(1)风险价值的多分辨率特征；(2)多尺度GARCH 建模理论与动态风险价值的计算；(3)风险价值的多尺度估值模型；(4)基于小波局部阈值的Copula密度估计及VaR 计算。

文献分析表明目前Copula-GARCH 模型是金融应用的热点。对模型估值而言，从贝叶斯的角度认为MLE 等方法都是假设模型参数具有确定的先验分布结构，不受样本观测值的特征所影响。譬如，在相依结构分析中，资产收益率分布的尖峰、厚尾、非对称等特征随着金融信息的冲击而发生迅速的突变，影响到相依结构中参数的后验变化。总体而言，MLE 方法对参数先验分布不变的默认假设欠妥，因此本书第二部分将MCMC 算法引入到资产相依结构分析，对时变Copula-GARCH 模型的参数进行MCMC 估计，通过MCMC算法逐步实现对相依结构模型参数时变性的后验学习，以此达到对资产潜在相依结构的最佳量化与解释及其对风险度量和预测等目的。因此本书第二部分设立两个研究问题：(5)时变Copula-GARCH-t模型参数估计与VaR度量；(6)时变Copula-GARCH-M-t模型与VaR 的预测。

我们认为设立以上六个研究问题，可以有效地紧扣本书的选题展开理论模型和方法的研究。宏观上：六大问题以VaR 计算为中心；微观上：依据小波分析和MCMC可以划分成两部分(问题1～4和问题5～6)；也可以按小波分析和Copula分成两部分(问题1～3和问题4～6)。问题1～2是离散情况下对资产收益率特征及风险价值的多分辨率研究，分别基于CAPM 模型和GARCH 模型；而问题3～4是连续情况下对资产风险价值的多尺度估值，分别基于阈值理论和Copula相依结构理论。问题5～6是时变情况下资产组合风险价值的量化分析，分别基于MCMC算法和Copula相依结构理论。