金融风险价值量化分析中VaR计算精度的改进研究成果

1.VaR 模型

四种风险度量方法分别是名义数额方法、因子敏感分析法、损失分布度量法和情景分析法。其中损失分布度量方法在金融风险度量中应用最为广泛，而风险价值模型(VaR)是最常用的风险度量与管理工具。早在1993年，G30集团发表了《衍生产品的实践和规则》的报告，提出了度量市场风险的VaR(Value-at-Risk)，随后由J.P.Morgan推出计算VaR 的Risk Metrics风险控制模型和风险计量系统(Risk Metrics system)已成为量化市场风险的一个免费的技术系统。VaR 度量风险的简单性、科学性、实用性和准确性，受到国际金融监管机构的普遍欢迎，并且与情景分析、压力测试和返回检验等一系列技术形成了风险管理的VaR 管理体系。1995年4月巴塞尔协议正式将VaR 模型作为银行业风险管理的一种有效工具推荐，由此实务界和学术界很快开始了基于VaR 方法的风险度量研究。各种改进和提高VaR 计算精度的研究成果不断出现，以此降低模型选择的风险，这一阶段相关文献成果可见Jorion(2007)的著作。

VaR 是指在一个风险范畴内资产头寸在一段持有期内潜在损失值的统计估计(Tsay，2005)。对VaR 的一般阐述可见Duffie and Pan(1997)。Rockafellar(2002)研究了一般损失分布下的VaR 和条件VaR 的最优化计算问题。因此根据计算方式的不同，VaR 估值研究划分为参数法、非参数法和半参数法等。

参数法是一种重要的计算方法。根据损失分布的密度函数的解析式可以直接计算VaR 的值。这是VaR 的主流计算方法，譬如JP.Morgan的Risk-Metrics方法(longer stagey and more，1995)。Manganelli and Engle(2001)指出计算VaR 的关键在于如何准确地估计收益率的分布密度和联合密度。由于20世纪90年代金融时间序列计量理论的发展与成熟，VaR 的参数法主要以时间序列计量模型为主(Tsay，2005)，因此VaR 的估值精度受模型结构设定和参数统计推断的影响。随后学术界提出了许多改进VaR 计算精度的方法。Glassman等(2000，2002)假设资产收益率服从多元正态分布并运用Delta类和Gamma 类方法近似地计算了资产组合的VaR；Angelidis 等(2004)和Christoph等(2006)利用GARCH 类模型计算了资产的动态VaR，还评估了七个工业化国家股市指数的动态风险；Bhattacharyya等(2008)将新息(innovation)分布设为Pearson IV型分布，改进了GARCH-N模型对动态VaR的估值精度；Sadefo(2009)假设资产收益率的风险因子服从混合正态分布，利用动态条件相关(DCC)模型计算了组合的VaR。最近几年来，基于Copula函数及金融计量模型的VaR估值方法已成为金融风险度量与管理的前沿(图1.3)。同时国内学者紧随国际趋势在这方面的研究成果也很丰富(马超群等，2000和2001；朱宏泉等，2002；余素红等，2004；陈荣达等，2004；姚京等，2005；迟国泰等，2006；陈守东等，2007；林宇等，2009；王春峰，2001；樊智，2003；邵欣炜，2004；田萍，2005；何旭彪，2006；叶五一，2007；蒋翠侠，2009；张运鹏，2009)。

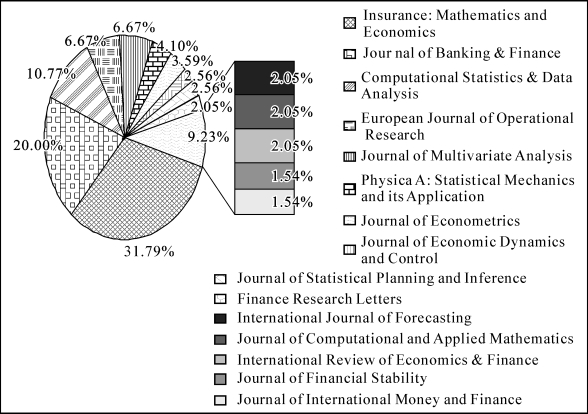
图1.3　VaR 文献分布(1995.6—2011.6)

参数法易受模型的选择和统计推断的影响。当样本量足够大时，半参数方法和非参数方法能在一定程度上克服参数法存在的这些不足，为此极值理论、Copula技术等新方法被引入改进VaR 的计算精度。Ramazan等(2004)利用极值分布计算资产收益率的VaR 并对新兴市场指数的实证分析，显示该方法明显改进了VaR 的估值精度；Miller等(2006)利用混合边缘分布的Copula函数计算组合的VaR，发现Copula是研究资产风险的尾部相依结构的有力工具；Fan等(2007)研究了高频金融数据的跳跃和波动的多尺度特征，同时分析了动态VaR 的统计特征；Vladimir(2009)将变点检测技术用于分析变点对VaR 的估值影响，发现收益率序列中存在的变点降低了VaR 的计算精度。从以上文献对VaR 的改进可见：极值理论主要针对样本极端值分布情况建模；Copula是对样本之间关联性建模的有效工具，但忽略了局部特征对VaR 的估值影响；小波分析方法仅仅应用于检测样本内潜在的变点，并没量化变点对风险度量的影响。为此在VaR 的计量方法中引入一些新的元素，克服已有计算方法的缺点以及发现一些新的实用结果，这仍是很有意义的研究工作。

2.GARCH 模型

GARCH 等金融计量模型(还包括SV 类模型)主要用于金融资产收益率波动的建模分析与预测。波动率在金融量化分析中很重要(Tsay，2005)，在金融衍生品定价中决定了期权的价格。同时波动率在金融风险度量中是一个关键的潜变量，根据计量模型计算头寸的动态风险VaR 时，基于GARCH 模型的时变波动率建模简化了VaR 的计算。下面主要从一元和多元两方面回顾GARCH 模型的研究进展。

对单变量模型而言，Engle(1982)提出的ARCH 模型及Bollerslev(1986)将其推广所得的GARCH 模型在理论界和实务界都得到了广泛的运用。关于ARCH 类模型的综述可见Bollerslev 等(1992，1994)，Bera and Higgins(1993)，Shephard(1996)等。Duan(1997)将GARCH 模型拓展到了增广GARCH-M 模型，并讨论了该模型参数估计的统计渐近性。随后又有很多功能性的衍生模型不断地被设定并得到了实证检验，譬如FIGARCH、FIEGARCH、ARFIMA-FIGARCH 等。张世英和樊智(2004)系统地回顾了已有ARCH 类模型及其建模方法，并将Duan(1997)的模型拓展到了增广FIGARCH-M 模型，包容了已有的各类GARCH 模型，还给出了具体的互化条件。其中增广FIGARCH-M 模型具有十分强的综合能力，包容了已有文献涉及的各类GARCH 模型，通过改变模型的均值方程和波动方程的结构以及标准化新息分布，可以得到既具体又灵活的波动模型，因而增广FIGARCH-M模型较好地量化了资产收益率波动的持续性、聚集性、非对称性、溢出效应及均值回复等随机特征，因此单变量GARCH 模型在国内外得到了广泛的应用(图1.2(a1)(a2))。

对多元GARCH 模型而言，最初在1980年代后期被提出，在1990年代上半期得到了推广。由于当时受到计算水平的限制，相关的研究工作在1990年代后停滞不前，随后经历了一个快速扩展期。Franses and van Dijk(2000)，Gourieroux(1997)等对GARCH 模型做了几乎全面的综述。多变量GARCH的近期理论综述可见张世英和樊智(2004)及Bauwens 等(2006)。其中Bollerslev et al.(1988)，De Santis and G'erard(1998)，Hafner and Herwartz(1998)等早期摄入的MGARCH 模型是单变量GARCH 模型的向量化，主要针对多元时间序列协方差矩阵的时变机制建模。由于模型参数较多，不便于参数估计，随后又有很多简化结构的模型被提出，如Tse and Tsui(2002)的DCCT 模型、Engle(2002)的DCCE 模型。与这些模型不同的是Jondeau and Rockinger(2006)的Copula-GARCH 模型由Copula函数连接一元GARCH模型，将前面的多元模型分解为单变量模型和相依结构模型，大大简化了多元模型的估计难度。因此这类模型在资产定价、投资组合构建与评估、期权定价、期货套期保值和风险度量与管理等金融研究中得到了广泛应用。与一元金融波动模型相比，多元金融波动模型的难点主要在于要求更精确地刻画多变量之间的相依模式，在此方面Copula函数可以发挥一定的作用。近几年来，Copula理论与GARCH 模型的融合为金融风险量化分析的相关研究添加了新的工具(Cherubini等，2004；Jondeau and Rockinger，2006；Patton，2006；Genest等(2009)；Concepcion and Hedibert，2010；韦艳华，2004；李伟，2008；任仙玲，2009；赵丽琴，2009；王晨，2010；傅强，2011；彭选华，2011)，同时得到了学术界和实务界的高度认可和普及(图1.2(c1)(c2))。

3.小波分析(www.xing528.com)

法国科学家Morlet和Grossman 于20 世纪30 年代提出的小波分析(Wavelet Analysis)已成为一种强有力的数据分析工具，被广泛用于信号处理。在图像处理、模式识别、地质勘探、医学诊断、数值计算等方面受到众多学者的关注和应用。小波函数具有良好的时频局部化性质，能够量化研究对象的局部近似和细节特征，进而小波分析被称为数学显微镜，为此小波分析及工程应用的文献很多(Grossmann and Morlet，1984；Mallat，1989&1998；Chui，1992；Hardle，1998；Vidakovic，1999；Percival and Walden，2000；Nason，2008)，然而在经济、金融等学科方面的文献相对较少(Whitcher，1998；Gencay等，2001；Ramsey，1999&2002；Patrick，2005)。随着经济学科的交叉性和复杂度的提高和信息技术的普及，经济、金融数据涵盖的信息量愈加丰富，影响因素也愈加隐蔽，普遍具有非线性、时变性和非平稳性、联动性等随机特征，这使得经典计量理论的建模分析及信息解读等功能受到了很大的挑战。小波分析独有的时频局部化的“显微镜”功能使得从不同的时间尺度对经济与金融数据进行分解和重构成为可能，这有助于经济、金融现象的研究和挖掘样本潜在的关键信息，从而准确地把握市场的演化趋势。因此，近十年来小波分析在金融、经济的实证分析中的文献有较强的增长趋势(图1.2(b1)(b2))。下面主要评述与本书研究工作相关的小波多尺度分析及阈值理论的研究近况。

多尺度分析源于小波分析在信号处理中的应用，最初诞生于Mallat(1989，1998)提出的一组正交小波基多尺度逼近L2(R)空间及计算小波系数的塔式算法。多尺度分析是一个极富应用潜力的数据分析工具(Percival and Walden，2000)。近几年来，国内学者主要涉及金融波动分析、多分辨率协整分析、多尺度套期保值模型、多尺度跳跃识别与波动率估计、多尺度GARCH检验、金融时序变点检测、风险价值的多分辨率特征研究、股指期现货时变相依结构的多尺度特征研究等应用(徐梅和张世英，2005；许启发等，2007；王春峰等，2009和2011；Peng and Fu，2009；傅强等，2007和2010；彭选华等，2007和2011)；而国外学者应用于经济变量尺度关系分解、格兰杰因果检验、面板序列相关性检验、单位根估计、长记忆估计、时序变点检测、波动溢出、时变风险传染与分析等金融计量问题研究(Ramsey，1998；Ramsey，2002；Lee，2001；Hong，2001&2004；Fan，2010；Jensen，1999&2000；Whitcher，2004；Chen等，2008；Gençay，2003&2010；Fernandez，2006；Conlon，2008&2011)。

对小波多尺度分析而言，阈值理论是另一个重要的研究领域。随机变量分布密度的解卷问题得到了学术界的普遍关注，使得阈值规则成为“统计建模与小波应用”的热点课题。Donoho等(1993，1994)对经验小波系数的全局阈值收缩，讨论了阈值算法对未知光滑度的密度函数的自适应性和小波收缩的渐近性。Vidakovic(1999)在《小波分析与统计建模》一书中总结了这一领域近十年的研究成果。密度估计与解卷积的关键是对经验小波系数取阈值，经过取阈值后重构的密度函数必然与真实密度之间存在误差。大量文献剖析了不同函数空间中基于各类阈值规则的密度估计误差的收敛性。Cohen 等(2001)给出了极大值空间(maximal spaces)中一类阈值算法的误差收敛速度。Chicken等(2005)提出了密度估计的块阈值算法，并证实了该算法的局部和全局自适应性。Kerkyacharian 等(2001)讨论了阈值算法关于最大集(maxset)或最大最小(minimax)准则的收敛性。Autin(2006，2008)给出了实数集R 上的密度估计子的最大集，还分析了最大集上的μ 阈值规则。Chesneau等(2008)在最大集上比较了硬阈值和软阈值规则的估计效果及误差的收敛速度。Donoho等(1996，1998)首次提出基于全局阈值规则的密度估计的小波方法，并在最小最大值准则下发现，误差收敛速度的关键因素是样本容量和密度函数的光滑度。Kerkyacharian等(1996)在Lp范数下讨论了密度小波估计的自适应性，这是均方意义上的误差收敛性分析的拓展。Pensky等(1999，2009)提出了非参数密度解卷积的自适应小波估计子，比较了线性阈值估计子和非线性阈值估计子的收敛性，基于Meyer小波的数值算例，证实了后者比前者的估值精度高，而且误差快速收敛，随后还将其推广到了求解基于周期小波的泛函密度解卷问题。Bigot等(2009)利用小波阈值方法，求解对数密度函数的卷积问题。Meyer函数被用于计算小波系数，随机块阈值方法用于对经验小波系数进行修正，数值算例表明该方法具有局部自适应性，但收敛速度仍受密度函数的光滑性和样本容量的影响。

总体而言，小波阈值理论研究近况划分为四个阶段：(1)在L2(R2)空间内概率密度函数的小波线性阈值估计，对估值误差收敛性的分析以误差的二范数度量，关于阈值规则的设定主要是全局阈值方法，仅包含硬阈值和软阈值两种主流规则；(2)将L2(R2)空间内概率密度函数的估计结果拓展到Holder空间、Soblev空间及Besov空间，从而空间的光滑性越好，估计误差的收敛速度越快；(3)从最优化的角度研究密度的小波估计，先后提出了误差最小化的minimax方法和更一般的maxset方法；(4)将Besov空间的成熟结论应用到跨领域的研究。

以上两方面的文献说明，正如现代经济学的发展推动了计量经济学的一些估计和检验方法的不断改进和完善，而小波分析方法在金融计量学中的应用便是其中的一个重要事实，虽然许多学者在这方面做出了杰出的贡献，取得了令人欣喜的研究成果，但这里仍然还有很多重要工作去做，譬如强化小波多尺度分析和阈值理论对资产价格波动特征及金融风险度量的应用研究。

4.Copula理论

最早由Sklar(1959)提出的Copula函数将多元变量的联合分布函数分解为各变量的边缘分布函数和一个Copula函数。这为多元变量的联合分布建模提供了一种新的统计方法。从统计建模的角度上看，Copula函数的引入使得对多元变量的联合分布建模可以分为如下两个方面：一是准确地选择边缘分布模型以更好地拟合各变量的边缘分布统计特征；二是选择合适的Copula函数刻画变量之间的相依结构。在早期，Copula理论的研究主要集中在统计性质的研究。随着全球金融业的发展与计算机软件技术水平的进步，直到近10年来很多文献探讨了Copula函数的广泛应用。这主要包含在金融风险和信用风险度量、金融相依结构分析、金融衍生商品和结构型金融商品等的定价和风险管理等金融量化分析的各领域。(Rodriguez，2003；Embrechts，2003；Dias and Embrechts，2004；Hu，2006；Patton，2006；Jondeau and Rockinger，2006；Roch and Alegre，2006；Bartram，2007；Liu and Luger，2009；张尧庭，2002；韦艳华等(2004，2007)；张明恒，2004；刘金全等，2010；傅强，2011)。

图1.2(c1)(c2)分别是国内外对Copula理论在金融中应用的文献趋势，我们可以发现国内的研究明显滞后于国外的研究。但近几年来这种趋势差距在明显缩小，研究水平仍然不同，国内研究多以实证分析为主，涉及理论问题的研究相对较少。因此对Copula理论及其金融应用的研究作为本书摄入的一个研究点。

5.MCMC算法

金融计量模型估值方法主要有经典极大似然(MLE)方法和贝叶斯方法。两者区别主要在于：(1)MLE方法视未知参数为固定的值，参数的估计值可以由样本数据构造，通过最大化目标函数的似然函数进行模型估计，并且利用拟合的模型做出统计推断。而贝叶斯方法将参数视为随机变量且以一定概率的形式出现，然后利用贝叶斯公式，从先验分布得到后验分布并利用后验分布进行模型参数的统计推断。这曾经是经典统计学派和贝叶斯学派争论的主要焦点，但越来越多的经典学派统计学家已开始接受贝叶斯学派的观点，将未知变量看作随机变量；(2)贝叶斯学派认为事件的概率可视为根据经验做出的个人信念，可以利用先验概率合理地确定先验分布。而经典学派认为不能轻率地使用先验概率(茆诗松等，1998)。

计算机技术的进步提高了金融计量模型的统计推断与蒙特卡罗模拟分析的质量和精度，同时促进了相关的算法和模型应用的发展。这些文献主要包括Gelman(1992)，Geweke(1993&2004)，Nakatsuma(1998)，Bauwens(1999)，Walker(1999)，Deschamps(2006)，Rodrguez(2009)，Amelie(2011)等。我们发现蒙特卡罗马尔可夫链(MCMC)算法已引入到GARCH 等金融计量模型参数估计及金融问题的量化分析(Tony，2004；Tsay，2005；Gerlach，2006；Concepcion，2010；傅强，2011)。

图1.2(d1)(d2)分别是国内外对MCMC算法在金融中应用的文献趋势，可以发现国内的研究明显滞后于国外的研究。但近几年来这种趋势差距在明显缩小，研究水平仍然不同，国内涉及算法理论及金融计量模型参数估值的研究相对实证研究而言较少。因此MCMC算法理论及其金融计量应用也是本书的一个研究部分。