小学数学教育：教学思维与概念理解差异的心理学分析

表2-1是在不同教学思维的数学问题启发下，小学生对周长理解的各水平阶段的成绩统计。（类型1为以发散思维的数学问题启发学生，类型2为以集中思维的数学问题启发学生）

表2-1　不同教学思维下小学生数学概念理解成绩的差异比较（N=128）

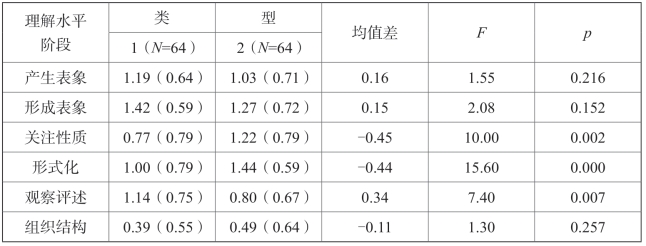
从表2-1可以看出，在产生表象和形成表象阶段，受不同类型数学问题启发，小学生的数学概念理解成绩不存在显著差异（p＞0.05），说明无论是受发散思维还是集中思维的数学问题启发，在这二个阶段小学生数学概念理解成绩几乎一样，即小学儿童对数学概念的理解没有不同。小学低、中年级学生以直观形象思维为主，“周长”概念比较直观，小学生容易产生和形成“一周长度”的表象，因此在概念理解的较低水平阶段，教学中无论采用发散思维的数学问题还是集中思维的数学问题启发学生，对学生理解数学概念的影响不大。(www.xing528.com)

在关注性质、形式化和观察评述阶段，受不同类型数学问题启发，小学生的数学概念理解成绩存在极显著差异（p＜0.01），其中在关注性质、形式化阶段，小学生受类型1数学问题启发时的数学概念理解成绩较受类型2数学问题启发时低，均值差分别为0.45、0.44；在观察评述阶段，小学生受类型1数学问题启发时的数学概念理解成绩较受类型2数学问题启发时高，均值差为0.34。说明教学中采用不同类型的数学问题启发学生，会影响他们对数学概念的理解。表现为在理解的中等水平阶段，集中思维的数学问题有助于小学生对数学概念的理解；在理解的较高水平阶段，发散思维的数学问题有助于小学生对数学概念的理解。这是因为在教学中，集中思维的数学问题指向概念的要点内容，能直接引导小学生使用“自然语言”思考概念要素，帮助他们抽象概念特性、建立形式化的数学对象，但这具体的指导对学生形成数学概念的“符号系统”帮助不大，即在理解的较高水平阶段对帮助小学生理解数学概念作用不大；发散思维式问题指向性不强，由于小学生的理解能力比较低和欠缺理解方法，他们理解概念时把握不了概念的关键，导致他们的数学概念理解成绩相对较低，但开放的思维能促进小学生对数学概念的全方位思考，有利于他们获得数学概念“关系和结构”的理解，使他们在较高水平阶段对数学概念有较好的理解。

在组织结构阶段，学生数学概念理解成绩很差，可以认为小学三年级学生对“周长”概念的理解水平未达到组织结构阶段，说明学生很难达到对数学概念深层次的理解。

总之，在概念理解的较低水平阶段，教师采用发散思维和集中思维的数学问题启发，对小学生理解概念的影响作用几乎一样；在概念理解的中等水平阶段，集中思维的数学问题有助于小学生对数学概念的理解。