由于数学史内容与其他三类数学文化内容在形式上有所区别,因此,我们把数学文化的运用水平分为两种形式。
1.数学史的运用水平
数学史的运用水平可以分为以下五类:[12][13](1)点缀式:采用图片形式,在正文中穿插或在阅读材料中呈现孤立的图片;(2)附加式:通过文字阅读材料,讲述数学故事、人物生平、历史背景等;(3)复制式:在正文各部分直接使用历史上的数学问题,如小学数学教材中引用我国古代数学名著《孙子算经》中的“鸡兔同笼”问题,见图2-7;(4)顺应式:在正文各部分将数学史上的数学问题进行改编,或利用数学史材料编制数学问题,以顺应当前教学的需要,如北师大版教材(北师大版五年级下册,第28页)将庄子的话改编成数学问题,见图2-8;(5)重构式:在正文各部分中将很多概念直接按照历史进行教学,可能并不自然,因而需要对历史进行重构,如小学数学教材中小数的教学,让学生先认识分数,再学习分数的产生及其意义,这其实就是根据数学历史、学生心理和数学逻辑重构的教学内容,见图2-9。三种版本教材中数学史的运用统计见表2-11。

图2-7 鸡兔同笼问题

图2-8 北师大版教材顺应式例子

图2-9 人教版教材分数的意义
表2-11 数学史运用水平的比较(单位:个)

由表2-11可知,三种不同版本教材中数学史运用水平出现最多的是“附加式”形式,占总体的60%以上,这些大多安排在“你知道吗?”“数学阅读”等栏目,正文中出现的相对较少。从上述统计数据来看,小学数学教材中的数学史主要采用直接运用的形式,间接使用较少。
2.其他数学文化的运用水平(https://www.xing528.com)
除数学史之外,数学文化的运用水平可以分为外在型和内在型,内在型又可细分为可分离型和不可分离型。外在型是指仅仅介绍数学文化本身,不涉及数学知识,如教材中介绍中国古代的钱币(苏教版一年级下册,第71页),见图2-10。可分离型是指数学文化与数学可以分离,如果去掉数学文化背景,也不会影响此数学问题,如关于松鼠尾巴长度的计算,在图2-11中若去除松鼠,或者换上其他的动物,不会影响到数学知识的学习(北师大版五年级下册,第27页);不可分离型是指数学文化内容成为数学问题的一个有机组成部分,运用数学知识解决具体的文化问题两者不可分离,如利用中国民间传统艺术剪纸来观察轴对称(人教版二年级下册,第31页),见图2-12,再如人教版一年级下册第一单元认识图形(二),教材在例3部分以问题解决的形式呈现七巧板的相关数学知识,见图2-13。参照以上分类方法,对其他数学文化内容的运用水平进行分类统计,见表2-12所示。
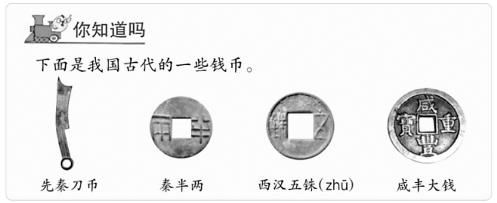
图2-10 中国古代钱币

图2-11 松鼠尾巴长度的计算

图2-12 剪纸中的轴对称
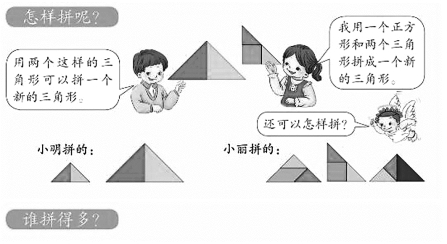
图2-13 七巧板的学习
表2-12 其他数学文化运用水平的比较

从表2-12可以看出,三种版本教材中数学文化的运用水平整体偏低,可分离型是主要的运用方式,达到70%以上,人教版甚至超过90%。这表明,教材中数学文化与数学知识的关联程度较低。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




