套利定价基本原理——证券投资实务

（一）假设条件

套利定价理论模型与资本资产定价模型一样有如下几个假设：①投资者是收益的不满足者，追求投资收益的最大化；②投资者是风险的厌恶者，回避风险；③市场是完全的，交易成本为0；④投资者在同一风险水平下，选择收益率较高的证券；在同一收益水平下，选择风险较低的证券。但是，资本资产定价模型中单一投资期、税负为0、投资者可以无风险利率自由地借入和贷出资金、投资者以收益率的均值和方差为基础选择投资组合的四项假设没有包括在套利定价理论之中。

套利定价理论不同于资本资产定价模型的基本假设有：①影响证券价格的因素不仅有风险，还有其他一些因素，但是对于一个充分多元化的组合而言，只有几个共同因素需要补偿；②具有相同风险和收益率的证券，不能有两种或两种以上价格；③每个投资者都会去利用不增加风险而能增加组合预期收益的机会。利用这种机会的具体做法就是使用套利组合。如果市场处于不均衡状态，市场上就有投资者可以利用的套利机会，而随着套利者的买进和卖出，套利空间将逐渐缩小直到消失，市场则进入均衡状态，从而形成均衡价格。

（二）套利机会与套利组合

通俗地讲，套利是指人们不需要追加投资就可获得收益的买卖行为。从经济学的角度讲，套利是指人们利用同一资产在不同市场间定价的不一致，通过资金的转移而实现无风险收益的行为。比如，如果你发现某种邮票在上海的卖价为1 000 元，而在深圳的卖价为1 200元，那么你会在上海以1 000 元买下该邮票，而后在深圳以1 200 元卖给他人，从而赚取一定的收益。这种行为就是套利，这种机会就是套利机会。又如，LOF 基金由于在交易所上市，又可以办理申购赎回，所以二级市场的交易价格与一级市场的申购赎回价格会产生背离，由此产生了套利的可能。当二级市场价格为1.25 元，基金公司的申购价格为1.21元，投资者可以从基金公司申购LOF 基金份额，再在二级市场卖出基金份额；如果二级市场价格为1.17 元，基金赎回价格为1.21 元，投资者就可以先在二级市场买入基金份额，再到基金公司办理赎回业务完成套利。

通过前面的分析可以看出，当套利机会出现时，投资者就会通过低买高卖赚取差价收益。这时，使套利机会存在的那些证券的定价是不合理的，因此市场上对这些证券的需求与供给就处于非均衡状态，其价格就为非均衡价格。随着套利的进行，这些证券的价格会随供需的变化而发生上升或下跌。当达到某种水平使套利机会不再存在时，套利者的套利行为就会终止，市场将处于均衡状态，各种证券的定价就处于合理水平。此时，市场不存在任何套利机会。这就是套利与均衡的关系，它是资本市场理论的一个基本论点。

在套利定价理论中，套利机会被套利组合描述。所谓套利组合，是指满足下述三个条件的证券组合。

（1）该组合中各种证券的权数之和等于零，即它是一个不需要追加额外资金的组合。

（2）该组合既没有系统风险，也没有非系统风险，即该组合因素灵敏度系数为零。

（3）当市场不均衡时，该组合具有正的期望收益率。

套利组合的表达式可用以下公式表示：

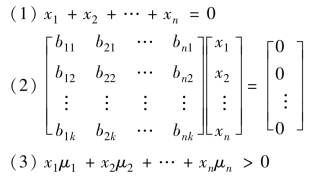
式中　xi——证券i 的投资权重；

　　　b——证券对因素（有k 个）的敏感性；

　　　μi——第i 个证券的期望收益率。

套利组合的特征表明，投资者如果能发现套利组合并持有它，就可以实现不需要追加投资又可获得收益的套利交易，即投资者是通过持有套利组合的方式来进行套利的。所以套利定价理论认为，如果市场上不存在（即找不到）套利组合，那么市场就不存在套利机会。

【例4.5】 假设投资者现在面对三只股票，并给定了三只股票的贝塔系数和预期收益率，如表4.2 所示，投资者应当如何构建套利组合，以获取无风险套利利润？同时请问无风险套利收益来自何处？

表4.2　三只股票的贝塔系数和预期收益率

分析：假设中石油的投资权重为x1，深万科的投资权重为x2，兰花科创的投资权重为x3。

第一步：令权重之和＝0，即

一般来说，如果资产组合中各项资产的权重之和等于1，意味着投资者将全部资金用于购买各种资产；而权重之和等于0，说明投资者不打算投入一分钱的自有资金。

第二步：令组合的β 系数＝x1β1＋x2β2＋x3β3＝0，即：

由第一步和第二步可以得出：

第三步：令组合收益率大于0，即：

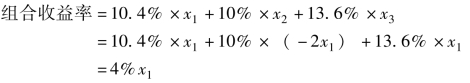
如果令x1＝50%，则x3＝50%，x2＝－100%，则

组合期望回报＝4%×50%＝2%。

投资比例＝－100%＋50%＋50%＝0；相当于没有花1 分钱，“空手套白狼”。

组合风险＝0.5×0.8＋（－1）×1＋0.5×1.2＝0，β＝0，说明组合无风险。

组合收益＝50×10.4%＋（－100）×10%＋50×13.6%＝100×2%＝2 （万元）

此时我们应当这样理解，某投资者身无分文，但是他通过研究发现中石油、深万科、兰花科创存在套利机会，因此，他决定向证券公司融券，借入市值100 万元的深万科，并将其抛出，从而套取现金100 万元。然后他利用这100 万元中的50 万元投资中石油，50 万元投资兰花科创。

那么2% 的无风险套利收益来自何处？

β 等于1 的深万科，收益率＝10%；β 等于0.8 的中石油，收益率＝10.4%；β 等于1.2的兰花科创，收益率＝13.6%。

显然，如果将50% 的资金投资于中石油，将50% 的资金投资于兰花科创，则由中石油和兰花科创构成的组合的β 等于1，其组合的收益率为12%。而深万科的β 等于1，但收益率只有10%。

系统性风险相同，β 等于1，但是深万科的收益率低（10%），应当卖出；中石油和兰花科创构成的组合的收益率高（12%），应当买入。

低买高卖的差价＝12%－10%＝2%。

（三）套利定价模型

1.APT 单因素模型

前面，我们已经了解了系统风险与非系统性风险。系统风险主要来自影响所有证券的宏观经济因素；非系统风险等于公司特有风险，来源于某个公司或某个行业。

正是由于这两类风险的存在，所以：

单因素模型认为证券收益率受到一种因素的影响，一般可以用下面的方程来表示：

(www.xing528.com)

式中　Ai——单个证券的预期超额收益率，即确定性；βiRm＋Ei表示偏离了预期的程度，即不确定性事件的影响。

　　　βi——宏观经济不确定性对证券收益率的影响程度。表示证券i 对宏观事件变动的反应。如同样是大盘下挫1%，大同煤业因此下挫2%，我们就说大同煤业的βi等于2。

　　　Rm——市场组合的超额收益率。

　　　Ei——意料之外的公司特有事件的影响。

例如，我们预计大同煤业2010 年的年收益率为15%，无风险利率为5%，所以大同煤业2010 年的预期风险溢价应该是10%。

而事实上，2010 年年底公布的大同煤业实际收益率是10%，实际风险溢价为5%。那么10% 和5% 是有差距的。这5% 的差距没有被预计到，这反映了不确定性事件的影响。

这种不确定性一方面是宏观经济的不确定性——系统性风险。例如，受经济不景气影响，大盘下挫2%，据估计，大同煤业的βi等于2，所以大盘下挫会造成大同煤业收益率下降2%×2＝4%。

另一方面是公司或行业的不确定性——非系统性风险。例如，市场预计大同煤业的华南区市场份额将上升1%，结果只上升了0.5%。这是一个好消息还是坏消息？是系统性风险还是非系统性风险？显然这是一个公司特有事件，是一个坏消息，对公司股票的影响是非系统性的，公司收益率因此下挫1%，大同煤业的实际风险溢价＝10%－4%－1%＝5%。4%＋1%即不确定性事件的影响导致了大同煤业实际收益率与预计收益率5% 的差距。

单个证券的总风险可以分解为两部分。

（1）系统性风险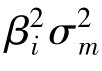。应当注意的是，每只股票所蕴含的系统风险不仅取决于Rm的波动性，即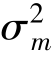，也依赖于单只股票收益率对市场收益率波动的敏感性。即系统性风险一方面取决于市场的波动性水平，另一方面取决于市场波动性会在多大程度上影响单个证券收益率的波动。如同样是金融危机导致纽约股市收益率下挫5%，但是IBM 和可口可乐受冲击的程度不同。IBM 可能只因此下挫3%，而可口可乐可能因此下挫7%，这说明可口可乐比IBM更容易受到市场波动的影响，因此它的系统性风险更大。

（2）非系统性风险。多样化程度增加可以降低投资组合的总风险。实际上是减少非系统性风险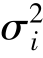，而非系统性风险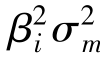大致不变。

2.APT 多因素模型

很多情况下，一个共同因素不足以反映证券之间的关联性。要想较好地反映影响证券变动的因素，就必须增加共同因素的数量，如经济形势的好坏会影响大部分公司，从而影响证券的预期收益率，但经济形式不是一个单一因素，它可能通过两个或两个以上的共同因素来影响证券的收益，例如国民生产总值的预期增长率、实际利率增长率、预期通货膨胀率、石油资源等的价格增长率。

通常，证券收益率受到若干个共同因素的影响：F1，F2，F3，F4，…，Fn等。这些因素对证券第t 期收益的影响可通过如下方程来表示：

式中　F1t，F2t，…，Fkt——对证券收益有共同作用的k 个因素第t 期预期值；

　　　βi1，βi2，…，βik——证券i 对这k 个因素的敏感性；

　　　εit——残差项；

　　　αi——其他因素为零时证券的预期收益率，也称零因素。

在多因素模型下，证券的预期收益率可表示如下：

因此，要计算证券的预期收益率，先要计算各证券的αi，βi1，βi2，…，βik等参数，还要估计出这些共同因素的预期值。

下面以中石油收益的要素为例，来说明以上公式的意义。

假定影响中石油收益的要素有三个：工业生产I、利率R、消费者信心C，其风险溢价如表4.3 所示。

表4.3　影响中石油收益的三个要素

则中石油的实际风险溢价计算公式为：

式中　R——中石油的实际风险溢价，即中石油的实际收益率减去无风险利率的超额收益率；

　　　I——工业生产的风险溢价；

　　　β1——工业生产对中石油收益的影响程度；

　　　R——利率的风险溢价；

　　　β2——利率变化对中石油收益的影响程度；

　　　C——消费者信心的风险溢价；

　　　β3——消费者信心变化对中石油收益的影响程度。

该公式说明，中石油的实际风险溢价包括三部分。

第一部分a 表明常数项，是预料之内的中石油风险溢价，也就是说，通常情况下，专家预计中石油的实际收益率是12%，无风险利率是5%，因此中石油的a 等于7% （预料之内的）。然而到了年底，中石油的实际收益率变成了15%，扣除无风险利率后，中石油的实际风险溢价是10%。显然，实际风险溢价10%－预期风险溢价7%＝3%。尚有3% 的差距是预料之外的。那么如何来解释多余的3% 的风险溢价呢？一方面可能是因为中国GDP 的实际增长率上升，或者大盘预料之外的上涨，总之是来自宏观方面的意外惊喜导致了中石油实际收益率的上涨，这属于系统性风险。另一方面可能是中石油本身的原因，如突然在山西发现了油田。来自中石油公司的意外利好消息导致了中石油实际收益率要好于预期收益率，这属于非系统性风险。即：

在不考虑随机因素的影响下，ε＝0，则中石油的预期风险溢价为：

在套利定价理论下，欲求得中石油的均衡收益率，前提是不存在套利机会，即a＝0。

可以推出中石油的预期均衡收益率E （R）：

则中石油的预期均衡收益率为：

类似于CAPM，在这16% 的收益中，无风险利率为6%，风险溢价为10%。