投资组合理论详解-《证券投资理论与实务》书评

（一）马柯维茨资产组合理论的基本假设

马柯维茨的资产组合理论建立在严格的假设之上。这些假设一类是关于投资者的，一类是关于资本市场的。

1.关于投资者的假设

（1）投资者基于收益率—风险，即均值—方差范式进行投资决策。期望收益率反映投资者对未来收益水平的衡量，而收益的方差则反映了投资者对风险的估计。

（2）投资者是理性的、风险厌恶的，其对收益率具有不满足性，即期望收益一定时，投资者选择风险程度较低的证券或证券组合；而在给定风险程度下，选择期望收益最高的证券或证券组合。

（3）独创性地提出投资者的目标是期望效用E （u）＝f （E （R），σ2）最大化，而不是期望收益最大化。其中E （R）、σ2分别为投资的期望收益与方差。

2.关于资本市场的假设

（1）资本市场是有效的，证券的价格反映了其内在价值；市场无摩擦，不存在税收和佣金、保证金、买卖差价等交易成本。

（2）资本市场上证券有风险，收益都服从正态分布，不同证券之间有一定的相关性。

（3）资本市场上证券无限可分，可买任意小数量的股票、债券；且任何证券的购买不影响市场价格，即资本市场的供给具有无限弹性。

（4）市场允许卖空。

（二）投资者的效用函数与无差异曲线

1.效用函数

所谓效用是指人们从某事或某物上所得到的主观上的满足程度，因而效用属主观范畴。效用可以用效用函数或效用的无差异曲线来表示。效用函数是一个数学表达式，它为所有可能的选择赋予了一个值。这个值越高，效用就越大，表达了经济实体对可了解的风险和期望收益率的偏好。一般来说，一个投资者的效用函数受许多因素的影响，但在一定的条件下，投资者的效用函数可以仅仅表示为期望收益率和标准差的函数，从而投资者可以只把期望收益率和标准差作为选择的目标。在这种情况下，可以用无差异曲线来表示投资者的效用。

2.无差异曲线

所谓无差异曲线，是指在由期望收益率和标准差为坐标轴的平面上，将期望效用值相同的点所连成的一条曲线。对某投资者而言，同一条无差异曲线上的不同投资组合给他带来的效用期望值相等。无差异曲线具有如下的重要性质。

（1）风险厌恶者的无差异曲线凸向横轴，即随着风险的增加，对于相同幅度的风险增加额，投资者所要求的风险补偿不断增加，即随着风险的增加，无差异曲线上各点的斜率越来越大。

（2）无差异曲线向右上方倾斜（或者说无差异曲线上各点的斜率为正值），即随着风险的增加，要想保持相同的效用期望值，只有增加期望收益率，也就是说，必须给增加的风险提供风险补偿。

上述两个性质是由投资者的永不满足及风险厌恶特性所导致的。

（3）无差异曲线是密集的，即任何两条无差异曲线中间，必然有另外一条无差异曲线。我们把某个投资者密集的无差异曲线构成的集合，称为无差异曲线群。

（4）在无差异曲线群中，越往左上方的无差异曲线，其效用期望值越大。

（5）任何两条无差异曲线不可能相交。

无差异曲线的上述性质可以保证对任一投资者来说，必然有一条无差异曲线与下面所讲的投资有效边界相切。每个投资者都有一条自己的无差异曲线，而且对每个投资者来说，这条无差异曲线是唯一的。

投资者对待风险和期望收益率的态度也可以从他的无差异曲线的形状来分析。较陡峭的无差异曲线反映了投资者对风险持较保守的态度，即为承受额外的风险需要较多的额外预期收益来补偿；相反，较平缓的无差异曲线则反映了投资者敢于冒险的精神，即为了获取额外的预期收益愿意承受较多风险。图4.1 展示了三种不同风险厌恶程度投资者的无差异曲线。

为了确定一个投资者的无差异曲线，一种办法是给投资者提供一系列假想的投资组合及相应的期望收益率和标准差，然后要求他选择一个最满意的组合。给定选择，投资者的无差异曲线的形状和位置就可以被估计出来了。

图4.1　三种不同类型风险厌恶程度投资者的无差异曲线

（a）高度风险厌恶；（b）中度风险厌恶；（c）轻微风险厌恶

（三）投资的可行集或机会集

投资的可行集或机会集是指资本市场上可能形成的所有投资组合的总体。图形内部即为可行集，任意投资组合所代表的一点都落在可行集边界上或边界内。一般情况下，可行集的左侧边界为一条双曲线的一部分，是向左凸的，如图4.2 所示。

图4.2　投资的可行集或机会集

为说明可行集的这个性质，我们先从两证券的投资组合进行介绍。

假设市场上仅有两种证券A 和B，证券A、B 构成了两证券投资组合p，其期望收益率和标准差σp表示如下：

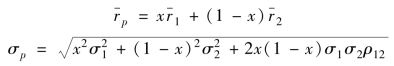
式中　、——证券A、B 的期望收益率；

　　　σ1、σ2——证券A、B 收益率的标准差；

　　　x——投资组合中证券A 的投资比重；

　　　1－x——证券B 在组合中的投资比重；

　　　ρ12——证券A、B 收益率间的相关系数。

当 x 不断变动时，就可以不断地得到新的投资组合。众多投资组合构成了投资组合的集合，即投资的可行集或机会集。

【例4.2】 假设市场上仅有两种证券A 和B，证券A、B 构成了两证券投资组合p，其＝2.5%，σ1＝2%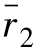，＝4%，σ2＝5%，当两种证券收益率间的相关系数ρ12分别等于1、0、－1 这三种不同的相关状态时，试画出不同相关系数下的投资可行集，并对各种相关状态下的投资组合可行集加以说明。当－1 ＜ρ12＜1 时，又是如何？

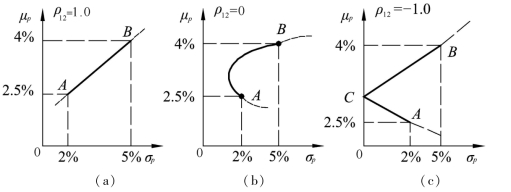
分析：不同相关系数下的投资可行集如图4.3 所示。

(www.xing528.com)

图4.3　不同相关系数下的投资可行集

（a）ρ12＝1 时的投资可行集；（b）ρ12＝0 时的投资可行集；（c）ρ12＝－1 时的投资可行集

（1）当ρ12＝1 时：

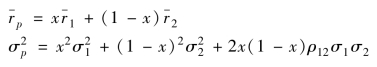
假设存在着证券卖空限制，则0≤x≤1，投资组合可行集为图4.3 （a）中的实线AB。如果允许对证券卖空，并将所得的价款及原有的资金投资于另一证券，即x 或1－x 小于0，并且x 或1－x 大于1，投资的可行集为图4.3 （a）中的实线和虚线。假如仅对证券B 卖空，则投资组合可行集是自点A 处延伸出去的虚线；假如仅对证券A 卖空，则投资组合可行集是自点B 处延伸出去的虚线。

（2）当ρ12＝0 时：

假设存在着证券卖空限制，即0≤x≤1，投资可行集为图4.3 （b）中的实曲线AB。如果允许对证券卖空，并将所得的价款及原有资金投资于另一证券，即x 或1－x 小于0，并且x 或1－x 大于1，投资组合可行集为图4.3 （b）中的实曲线和虚曲线。假如仅对证券B 卖空，则投资组合可行集是自点A 处延伸出去的虚曲线；假如仅对证券A 卖空，则投资组合可行集是自点B 处延伸出去的虚曲线。

（3）当ρ12＝－1 时：

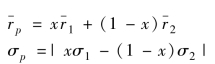
假设存在着证券卖空限制，即0≤x≤1，但xσ1－（1－x）σ2的符号不定。

当xσ1≥（1－x）σ2时，即x ≥，此时，σp＝xσ1－（1－x）σ2。

当xσ1≤（1－x）σ2时，即x ≤，此时，σp＝－xσ1－（1＋x）σ2。

这样，投资组合可行集为图4.3 （c）中的两条实线CB 和CA。如果允许对证券卖空，并将所得的价款及原有的自有资金投资于另一证券，即x 或1－x 小于0，并且x 或1－x 大于1，投资组合可行集为图4.3 （c）中的实线和虚线。假如仅对证券B 卖空，则投资组合可行集是自点A 处延伸出去的虚线；假如仅对证券A 卖空，则投资组合可行集是自点B 处延伸出去的虚线。

（4）当－1 ＜ρ12＜1 时：

整理后可得：

式中

当相关系数ρ12在－1 和＋1 之间时，可将ρ12＝－1 和ρ12＝＋1 的投资组合可行集同时标在图上，这构成了三角形ABC，如图4.4 所示。

图4.4　－1≤ρ12≤1 的投资可行集

由图4.4 可知，投资的可行集必然落在三角形ABC 中，如曲线ADB。ρ12越大，曲线ADB 就越靠近直线AB；ρ12越小，曲线ADB 就远离直线AB。ADB 是凸向纵轴的曲线，曲线上必存在一点D，离纵轴距离最近。

以上是两种证券投资组合的情形。如证券种类增至三种或三种以上，且各证券都是风险证券，此时的投资可行集是一个区域而不是一条曲线。按照类似的方法，可以构造多项证券组合投资的可行集。假设不得对证券卖空，则投资可行集为图4.5 上的点B、点C、点A、点D、点E 所围成的伞形区域，区域中的左边界BCA 曲线凸向纵轴。

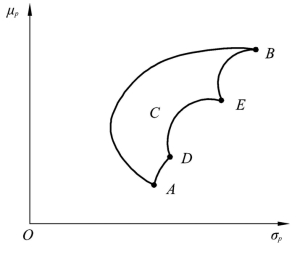
图4.5　多种证券组合的投资可行集

（四）投资的有效集或有效边界

由于风险厌恶者所追求的目标是既定期望收益条件下的风险最小化或者既定风险条件下的期望收益最大化，这一目标导致投资者在投资时应在风险和期望收益方面进行权衡。虽然有无数种可能的投资组合（即可行集）可供选择，但投资者不可能去评估市场上现存的每一种投资组合，这一工作简直是不可能完成的任务。实际上，投资者只需对一个被称为投资的有效集（The Efficient Set）或马柯维茨的有效边界（Markowitz’s Efficient Frontier）进行评估和进行选择即可。

一个投资者将从在各种风险水平上能够带来最大收益率的，以及在各种期望收益率水平上风险最小的证券组合集合中选择出最佳证券组合。满足这个定理的证券组合边界即有效边界。

这一定义中包含着如下两个条件：①给定的风险水平、期望收益率最大；②给定的期望收益率、风险水平最小。

满足上述条件的投资组合集合才是投资的有效集或有效边界。因此，投资可行集中的投资组合并非都是有效集中的组合。例如，图4.6 中的投资机会集左边界ACB，现在作一条垂线与曲线ACB 相切，切点为点C。在曲线ACB 的CB 部分为无效的投资组合。因为我们在曲线CB 上任取一点，如点B，与在曲线CA 上的点A 与点B 具有相同的风险（标准差），但点A 的投资组合的期望收益率要高于点B 投资组合的期望收益率。因而，理性的投资者会选择点A 的投资组合，而不会选择点B 的投资组合。因此，曲线CA 才是投资的有效集或有效边界。

图4.6　不具有无风险借贷机会的投资有效边界

很显然，投资的有效边界是向右上方倾斜的、凸向纵轴的曲线。另外，构成组合的证券间的相关系数越小，投资的有效边界就弯曲得越厉害。

（五）最优投资组合

所谓最优投资组合（The Optimal Portfolio）或最佳投资组合，是指某投资者在可以得到的各种可能的投资组合中，唯一可获得最大效用期望值的投资组合。利用投资者共同偏好规则可以确定哪些组合是有效的、哪些是无效的。特定投资者可以在有效组合中选择自己最满意的组合，这种选择依赖于投资者的偏好，投资者的偏好通过其无差异曲线来反映。通过前面分析，可知风险厌恶者的无差异曲线是递增的、凸向纵轴的，而投资的有效边界也是递增的，却是凸向横轴的，因此，无差异曲线与有效边界的切点是唯一的。该切点组合便是投资者最满意的有效组合，最优证券组合正是无差异曲线族与有效边缘的切点所在的组合。

现在将有效边界与无差异曲线放在一块进行分析，就可以确定最优投资组合了。图4.7中，曲线ABC 表示有效边界，投资者将在这条边界上选择某一点建立自己的投资组合。曲线①、②、③表示投资者甲的三条无差异曲线，而曲线④、⑤、⑥则表示另一投资者乙的三条无差异曲线。

对于投资者甲来说，点B 是最佳的效益组合，因为在这一点，他获得了最高可能的效用；对于投资者乙来说，点C 是其最佳的投资组合，同样在点C，乙获得了最高可能的效用。

以上分析表明，只要知道了投资者的投资偏好（通过无差异曲线的形状来反映），并且掌握了证券市场上的投资机会（由有效边界来表示），就有可能确定最佳投资组合。这就是投资者最高的一条无差异曲线与有效边界相切的那一点。

图4.7　最佳投资组合

需要注意的是，投资者在选择和建立投资组合的过程中，既受自身对待风险态度的影响，也受市场上现存投资机会的制约。一般情况是，投资者在有效边界与其尽可能高的无差异曲线相切之点上建立自己的投资组合，以使其投资效用水平或满足限度达到最大化。