证券投资组合的收益与风险度量达成结果

（一）证券投资组合的期望收益率

证券投资组合的预期收益是投资组合中所有证券预期收益的加权平均。记rp为投资组合p 的实际收益率，E （rp）或μp为投资组合p 的期望收益率，则投资组合中第 i 种证券的比例（权重）为：xi（i＝1，2，…，n）；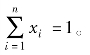

如果证券市场不允许卖空，则xi≥0；如果允许卖空，则xi≤0，可以为负。

投资组合p 的收益计算公式为：

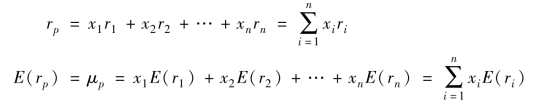
（二）证券投资组合的风险衡量

由于任何投资组合的本身都可以作为一单项资产来对待，因此，投资组合的风险也可用与单种风险证券的风险计量类似的方法进行计算。

任意两只证券i 和j，两者之间的协方差为：

两者的相关系数为：

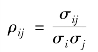
从而N 种证券的协方差矩阵为：

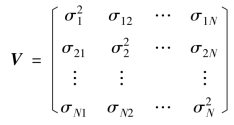
一个包含N 种证券的投资组合p 的方差为：

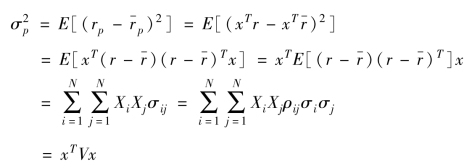
式中　x——权重列向量；

　　　——投资组合p 的期望收益率；

　　　——p 种证券的期望收益向量。(www.xing528.com)

对于只有两种证券构成的投资组合p 来说，其标准差为：

由此可以看出，投资组合的风险（方差或标准差）并非是构成组合的各种证券的风险（方差或标准差）的加权平均数。

（三）相关系数对证券投资组合风险的影响

从上述讨论已经知道，投资组合的风险与构成组合的各证券收益率之间的相关系数有很大的关系。为了便于分析，我们仅考虑两种证券投资组合，并且仅考虑相关系数是1、0、－1 这三种情况。多种证券构成的投资组合也有类似的规律。

由上述公式可知，当ρ＝1 时，有：

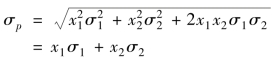
即，当构成组合的各证券的收益率成完全正相关时，投资组合的风险就等于构成组合的各证券的风险的加权平均数。在这种情形下，投资组合并不能带来风险的降低。同理，据公式可推出：当ρ＝0 和ρ＝－1 时，投资组合的风险都小于构成组合的各证券的风险的加权平均数，因而都在一定程度上降低了风险。

由此可以看出，除了构成投资组合的所有证券的收益率之间全都成完全正相关的极端情形外，投资组合的风险要小于构成组合的各证券风险的加权平均数，也就是说，投资组合具有分散风险的功能。实际上，同一股票市场的各种股票之间一般是正相关的，但相关系数小于1。所以，在这种情况下挑选出来的股票所构成的投资组合可以减少风险，但不能完全消除风险。

【例4.1】 已知证券组合P 是由证券A 和B 构成，证券A 和B 的期望收益、标准差以及相关系数如表4.1 所示。

表4.1　证券组合的期望收益、标准差及相关系数

那么，组合p 的期望收益为：

组合p 的方差为：

选择不同的组合权数，可以得到包含证券A 和证券B 的不同证券组合，从而得到不同的期望收益率和方差。投资者可以根据自己对收益率和方差（风险）的偏好，选择自己最满意的组合。