航天器发射技术：弹射内弹道基本方程

1.基本假设

弹射器的工作过程和现象比较复杂，很难建立完全真实的物理模型和数学模型，或者可以建立较准确的模型而解算困难。为解决实际工程计算问题，对于燃气式弹射器，常作以下基本假设，从而建立经典内弹道模型：

（1）火药遵循几何燃烧定律，即火药是按平行层或同心层规律燃烧的。

（2）高压室和低压室内的燃气具有高温特性，压强一般不是很高，可按理想气体处理。

（3）由于高压室中的气流流动速度远小于喷管中的气流流动速度，故可以认为燃气在高压室中无流动，各处燃气的压强、密度、温度等是均一的，即不考虑高压室压强等沿空间的分布，只考虑其随时间的变化规律。严格地说，火箭是在其底部压强或活塞底部压强的作用下向前运动的。由于火箭在弹射器内运动速度相对很低，燃气流动速度也很低，故可不考虑燃气在低压室内的流动，亦即不考虑低压室压强在空间上的分布，各内弹道方程中的压强一律采用瞬时平均压强来代替。这一假设也称为“零维”假设，是建立经典内弹道模型的根本假设。

（4）燃气在高压室喷管内的流动为一维、准定常、等熵的。

（5）燃气的成分，物理化学性质认为是固定不变的，这样与火药性质有关的量如爆温T0、定压比热cp、余容α和绝热指数k等均可看作常量。

（6）在高压室内部火药燃烧过程是绝热的。实际计算中，常用热损失修正系数χ1来考虑热损失。χ1的大小与高压室的材料和结构有关，且在高压室工作过程中应该是变化的。但由于散热损失只占装药能量的极小部分，其变化对内弹道计算结果影响甚微，因此对某个确定的高压室而言，可以认为χ1为常数，一般为0.9～0.95。

（7）在装药燃烧阶段，高压室燃气温度变化不大，可认为高压室燃气温度T1是常量，且T1＝χ1 T0。

（8）对因低压室壁热传导而引起的燃气能量损失（热散失）不进行直接计算，而是用降低流入低压室的燃气温度的办法予以考虑。

（9）低压室密闭性能良好，无漏气。

在以上假设条件下，弹射器性能计算将大为简化。虽然计算结果具有一定的近似性，但具有相当的合理性，在不要求特别高的精确度时，尤其适于工程上作快速计算。

2.基本方程

1）高压室燃气状态方程

根据基本假设，高压室按理想气体考虑，状态方程为

式中，mb为时间t内装药已燃去部分的质量，等于生成的燃气质量；mt1为时间t内高压室燃气的总流出量；p1为某瞬时高压室燃气压强；T1为高压室温度，T1＝χ1 T0，其中χ1为高压室热损失修正系数，T0为装药定压爆温。

设V10为高压室的初始容积，即高压室内无装药时的容积；ρp为装药密度；mp为装药质量；设ψ＝mb／mp，则某瞬时高压室中未燃火药的质量为mp（1－ψ），则已生成燃气可充满的自由容积V1为

2）燃气生成速率方程

根据几何燃烧定律（即火药按平行层或同心层燃烧），可得出燃气生成速率为

式中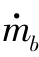，为每秒燃去的火药质量，即每秒燃气生成质量，也称为燃气生成速率；ρp为火药密度；Sb为某时刻火药所有参与燃烧的表面积，简称燃面；u为火药燃烧的线速度。

3）燃面变化方程

对于不同形状的火药，其燃面变化规律不同，需根据具体情况列出初始燃面和燃面变化方程。例如，对于两端面和外侧面包覆的多根单孔管状火药，有

式中，Sb0为t＝0时刻的初始燃面；Lp为火药长度；np为火药根数。

当时，火药在燃烧期间燃面保持不变，称其为恒面燃烧；当时，则为增面燃烧；当时，则为减面燃烧。

4）燃速方程

根据高压室常用的压强范围，火药采用指数燃速定律，燃速方程为

式中，u为火药燃速；a为燃速系数；n为燃速指数。

5）燃气流量方程

高压室燃气流量是指每秒通过高压室喷管出口流到低压室的燃气质量。根据气体连续方程，在喷管任一截面上的燃气流量是相等的，而喷管喉部为临界截面，在适当的条件下，该截面处气流速度恰为声速，即马赫数Mat＝1，这使流量表达式较为简洁。根据燃气在高压室喷管内的流动为一维、准定常、等熵的假设，有

式中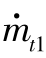，为高压室喷管喉部燃气流量，即高压室燃气流量；St1为高压室喷管喉部截面积；K0为与燃气比热比k相关的常量：(www.xing528.com)

式（3.3.3）表明，高压室燃气流量的大小取决于高压室压强、喷管喉部截面积和火药性能。当火药选定后，则流量只取决于高压室压强和喷管喉部截面积。

若令

称为流量系数，则

式（3.2.4）是在喷管没有摩擦和热损失的条件下导出的理想流量，因此与实际流量存在一定误差。这种误差可以通过引入流量修正系数予以修正，即

式中，φ21为高压室喷管的流量修正系数。

需要注意的是，拉瓦尔喷管内气体的流动状态还与外界反压有关。由于低压室内具有一定的工作压强p2，高压室喷管在具有较高反压的环境下工作，尚需根据反压比的大小判断其流动状态，从而确定其流量。

设pr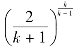＝，称为临界压强比。当（p2／p1）＞pr时，气体在整个喷管内作亚声速流动，喉部处马赫数Mat＜1，有

其中下标“e1”代表高压室喷管出口截面，Se1为高压室喷管出口截面面积。

在弹射器设计中，均保证高压室的工作压强为低压室工作压强的数倍，即使（p2／p1）≤pr的条件在弹射器工作阶段能够得到满足，只有在高压室的排气阶段才可能出现（p2／p1）＞pr的情况。

将上述两种情况统一写成

当高压室采用收缩喷管时，亦有亚临界、临界和超临界状态。虽然收缩喷管内的流动状态与拉瓦尔喷管中有差别，最后表达式与式（3.3.6）相同。

6）低压室燃气状态方程

在弹射器中，由于火箭不断向前运动，低压室容积不断扩大，属于变容情况，只能建立某瞬时的状态方程。低压室燃气视为完全气体，其状态方程为

式中，mt1为流入低压室的燃气质量；T2为低压室燃气温度；V2为低压室容积：

其中，V20为低压室初始容积（简称初容），即火箭未运动时的低压室容积；S2为低压室承压面积；l为火箭在弹射器内的行程。

7）火箭运动方程

在低压室压强大于起动压强后，火箭开始运动，此时火箭所受沿运动方向的外力包括弹射力、摩擦力等：

式中，∑F为火箭所受沿运动方向的合外力；Fe为弹射力；Ff为摩擦力；Fg为弹射质量的重力。

Fe是火箭在弹射器内受到的最主要的作用力，它是使火箭在弹射器内运动的推动力，可称为弹射力，由低压室压强形成，其大小为

摩擦力Ff的大小需根据发射筒、隔热尾罩或适配器等所选用的材料属性和配合关系，根据经验近似求得，或经过试验测得。

根据牛顿第二定律，火箭运动方程可表示为

式中，v为某瞬时火箭在弹射器内的运动速度。

火箭速度方程为

8）低压室能量方程

弹射器本质上是一种热机，低压室内的燃气对外膨胀做功，温度不为常量，需根据热力学基本定律求得其变化规律。

热力学第一定律的基本能量方程为

它是系统变化过程中能量平衡的基本表达式，任何系统、任何过程均可据此原则建立其能量平衡式。根据式（3.3.11）和基本假设，可得

式中，cp为燃气定压比热；cV为燃气定容比热；φ为次要功系数或称虚拟质量系数。