航天器发射技术中弹-装置系统的动态设计及分析

动态设计的主要任务是在已知战术技术要求的条件下设计经济合理的系统，满足各项战术技术指标，其中也包括可靠性、发射精度、动强度、疲劳寿命等与动态性能有关的各项指标的要求。

动态分析是根据给定的系统，建立数学模型，然后进行系统的性能分析，检查响应和其他与动力学有关的状态变量能否满足技术要求。

经常称动态设计为动力学的反面问题，动态分析为动力学的正面问题。

尽管理论上提出了一些动态设计的方法，但用于解决复杂结构的动态设计问题还存在较大的困难，所以一般将动态设计问题转化为动态分析问题来处理。根据经验或参照已有的同类系统设计一个初拟系统，然后进行动态分析，把分析计算的结果与设计要求相比较，找出差距，修改初拟系统，再分析比较和修改直至获得满意的结果为止。

弹－装置系统的动态设计过程如图3.10所示，图3.10表明初拟系统设计时要用系统观点，在考虑动态性能的同时全面考虑战术技术条件提出的各方面要求，其中特别是导弹和发射装置之间的联系和相互制约关系。发射装置方案设计还要考虑机动性、火控和勤务使用方面的要求。

动态分析输入的主要参数如下：

（1）发射装置结构参数包括几何参数和物理参数，包括质量、质心、转动惯量、刚度、阻尼等；

（2）导弹结构参数包括几何参数和物理参数，包括质量、质心、转动惯量、刚度、阻尼、推力特性、推力偏心、质量偏心、动不平衡等；

（3）系统要求包括运输工具、导弹数量、射速、质量、尺寸观测和瞄准要求等。

动态分析的输出是系统响应，如导弹脱离约束瞬间的扰动角、角速度、质心速度、动反力、动挠度、振动频率、振动衰减时间等。

1.发射动力学分析模型的建立

在完成图3.10所示的动态设计过程中，建立发射动力学分析模型是关键问题。

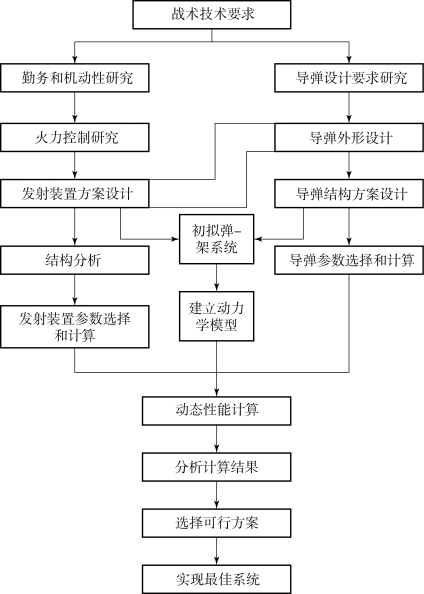
图3.10　弹-装置系统的动态设计过程

本小节所述的建模问题，是指建立理论分析模型。首先建立物理模型，即将实际系统简化成一个能够反映系统动态特性的结构简图。系统的固有动态特性主要取决于系统的质量、刚度和阻尼的分布特性。系统响应不仅和系统固有动态特性有关，而且和激励（输入）有关。建立物理模型时，还要确定主要激励及其物理特性。发射动力学是一门应用科学，因此物理模型既要能准确地反映实际系统的动态特性，又要便于用力学和数学工具进行振动分析和数字仿真。为了建立能够较好地反映系统实际情况的物理模型，设计人员对系统结构和动态设计要求应有深刻理解。

2.模型检验

运用物理和数学模型，通过计算机仿真，预示系统响应，有时对研制工作可以起指导作用。如何检验理论模型的分析误差，在工程设计中，受到技术人员的普遍关注。对模型的检验可分成两个阶段：第一阶段是指在原理样机制成以前用理论分析的方法检验理论模型；第二阶段是指通过对原理样机的测试结果检验理论模型。

1）第一阶段的检验方法

（1）将理论模型的数字仿真结果和将理论模型的阶数提高以后的仿真结果对比。如果差别在允许的范围以内，表明理论模型是准确的。

（2）求近似解析解，将近似解析解和数值解对比。如果两种解的趋势相同，一些特征点的数值相近，表明数值解有相当的可信度。

显而易见，上述两种方法都是用理论所求的数值检验理论模型，因此有一定的局限性。但在无法取得实测数据的条件下，也不失为可供选用的检验方法。

2）第二阶段的检验方法

（1）响应对比法。利用原理样机发射试验测试系统响应（如发射筒的振动参数、导弹的初始扰动参数、发射车底盘的振动参数等），将实测结果和理论模型的仿真结果对比，检验理论模型。此种方法在研制过程中已被广泛应用。

（2）模态分析法。首先检验系统固有动态特性，表征系统固有动态特性的是系统模态参数。系统模态参数是指系统的各阶振型（又称模态向量或特征向量）和各阶固有频率（又称特征值）。为检验系统固有动态特性，需要将原理样机通过试验模态分析得到的模态参数和利用理论模型计算所得的模态参数对比，如果在感兴趣的频段内模态参数的误差在允许的误差范围以内，则表明系统的结构模型能够反映实际结构的固有动态特性。利用现有的求特征向量和特征值的通用程序，可以求得理论的结构模态参数。为了求得原理样机的模态参数，需要选择一个已知的激励（如正弦激励、脉冲激励、随机激励等），通过信号发生器、放大器和激振设备施加于原理样机，与此同时，测试系统响应。在激励和响应已知的情况下，可以通过已有的通用模态分析软件，识别原理样机的模态参数。上述工作能够有效地检验系统的结构模型，除此以外，为使理论模型所求得的响应能够和实际系统响应相同，还需要检验激励模型。在原理样机的模态参数已知的情况下，通过测试原理样机在发射试验时的响应值，可以利用已有软件识别出原理样机在发射过程所受的激励，经过和理论的激励模型对比可以检验激励模型。

模态分析法比响应对比法能更深入地揭示理论模型和实际系统的差别，为修改模型提供更有利的依据，但模态分析法需要专用设备和软件。

3.低频分析模型

根据激励的频率，可以将发射动力学分析模型分为低频分析模型和中、高频分析模型，这类模型主要用于建立弹－装置系统的模型。目前应用较多的是多刚体模型和刚柔耦合模型，这两种模型主要用于分析低频激励下的发射动力学问题，包括在发射过程中如何避免共振、控制振动引起的初始扰动和发射系统主要构件强度是否满足要求等问题。下面简述3.1.6小节中列举的两种发射方式的发射动力学分析模型的建立和求解。

1）自力箱式倾斜发射的巡航导弹

为不使数学模型过于复杂，将图3.4所示系统的物理模型作尽可能的简化，简化后的物理模型如图3.11所示。

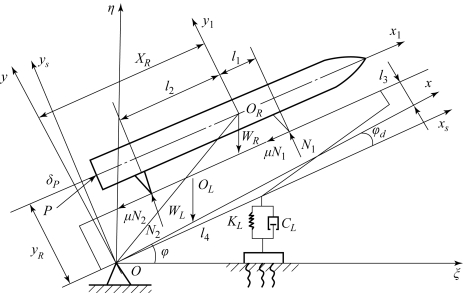
图3.11　物理模型

（1）物理模型。

①发射箱和导轨固连为一体，在图中只画出导轨，其质量、质心和转动惯量等于发射箱和导轨复合结构的参数。

②发射箱的通气面积足够大，自力发射燃气流排导顺畅，不考虑发射箱内燃气流对系统的激励。又因为是单发发射，导弹出箱以后，燃气流对发射装置冲击引起的振动对导弹已无影响，所以也不考虑导弹出箱以后的燃气流冲击力。

③导轨平直，发射过程中弹、轨之间没有惯性力作用。

④车体因为采用4个刚度较大的千斤顶支承，视其为固连于地面的刚体，自由度为零。

⑤将弹－装置系统视为在射面内的平面系统。

综上所述，在全约束期导弹相对于导轨有一个移动自由度，导弹和导轨绕耳轴有一个俯仰转动自由度。

（2）数学模型。

分析时选用下列坐标系：

Oξη为惯性坐标系，O点在耳轴，上耳轴与海平面平行。

Oxsys为发射装置基准坐标系，表示发射装置的初始位置，φ为高低瞄准角。

Oxy为发射装置坐标系，固连于发射装置之上，最初与Oxsys坐标系重合，振动时与发射装置一起运动，φd为发射装置相对静平衡位置的扰动角。

ORx1 y1为弹体坐标系，固连于弹体上，OR为导弹的几何中心初始平衡位置时ORx1轴平行于Oxs轴，发射过程中ORx1轴与Oxs轴夹角为导弹的扰动角θd。

导弹质心及定向钮在这些坐标系中的位置可以根据图3.11确定。导弹质心在Oxy坐标系中的坐标为（xR，yR），开始位置为（x0，y0），在Oxsys坐标系中的坐标为（xs，ys）。

任意瞬时导弹质心y向的坐标为

全约束期导弹的扰动角为

由于φd较小，导弹质心在Oxsys坐标系中的位置可近似写成

将式（3.1.12）及式（3.1.13）对时间t求二阶导，得

由于φd、δP（推力偏心角）是微量，故在下面的计算中忽略这些量的二阶量。(www.xing528.com)

作用于系统上的外载荷有：WR为导弹重力；P为发动机推力；δP为推力偏心角；WL为发射装置重力：CL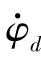为振动阻尼力，CL为阻尼系数；KLφd为弹簧恢复力，K为弹簧刚度系数。

各力的作用位置如图3.11所示。

（3）定向钮载荷的确定。

定向钮载荷是导弹在发射过程中作用在导轨上的力，它是进行发射装置强度、刚度设计所必需的数据。下面研究发射过程中导弹的运动。N1、N2为前、后定向钮载荷；Fμ为摩擦力，Fμ＝μ，μ是摩擦系数。此力作用于定向钮与导向面之间，平行于导弹的纵轴。于是导弹的运动方程为

式中，mR为导弹的质量；JRz1为导弹的赤道转动惯量；Mδ为推力对质心的力矩，称为推力偏心矩；φ为发射装置的俯仰瞄准角。

根据假设，整个系统开始时是静止的，即处于静平衡位置。因此，当推力达到下列值时开始计算时间，即

所以，整个系统在t＝0时导弹由静止开始运动，这一点作为解运动微分方程的初始条件。

用l2乘式（3.1.15）的第2式两边，并令sin（φd＋δP）≈φd＋δP，cos（φ＋φd）≈cosφ，再与式（3.1.15）的第3式相加，整理后得

式中，l0＝l1＋l2。

同理可得

式（3.1.16）和式（3.1.17）是导弹在导轨上运动时定向钮载荷的计算公式。

（4）导弹运动参数的计算。

①导弹在全约束期内的运动参数。导弹前、后定向钮在定向器上运动的时期叫全约束期。这个时期的运动参数由式（3.1.12）、式（3.1.13）和式（3.1.15）确定。但6个方程中有8个未知数——xs、xy，θd、y0、xR、φd、N1及N2，需要再补充方程才能解出全部未知数。

导弹沿x方向的运动参数xR及受φd影响甚小，故略去此项。式（3.1.15）中第1式变为：

由上式可以直接求解xs（t）值，解上述方程时可取摩擦力Fμ为常数，不考N1及N2变化的影响，所得结果足够精确。下面建立补充方程，以便求解其余未知数。

导弹的振动规律由整个系统的运动方程求解。利用动量矩定理可建立这一方程。

发射装置绕固定轴转动，动量矩为

式中，JL为发射装置对过O点的固定轴zs的转动惯量。

导弹平面运动，对固定轴的动量矩为

所以系统动量矩对时间的导数为

将式（3.1.12）～式（3.1.14）代入式（3.1.19）中，略去φd和θd的二阶小量，最后得

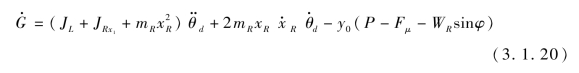
现在求系统上的外力对O点的力矩，由图3.11可知

式中，φ0为系统处于平衡位置时弹簧的转角；xL、yL为发射装置质心的坐标。

当导弹在发射装置上处于起始位置并且发动机未点火时，整个系统处于静平衡状态。这时的弹簧力矩应与系统的重力矩平衡，因此系统的平衡条件是

将式（3.1.22）代入式（3.1.21）中，得

因为在静载荷条件下，发射装置不可能产生过大的位移，略去φd的作用，并将式（3.1.11）代入上式，得

将式（3.1.13）代入上式，再和式（3.1.20）同时代入动量矩方程式之中，经整理后得

上式中仅xR及θd是未知数，解方程式（3.1.12）、式（3.1.13）、式（3.1.18）及式（3.1.23）就可得到导弹的运动参数。

②导弹在半约束期内的运动参数。导弹前定向钮已滑离，后定向钮仍在定向器上运动的时期叫半约束期，在半约束期N1＝0。摩擦力仍认为平行于弹轴，且为已知的定值。但这时的摩擦力只有后定向钮处一项，忽略它的作用亦可。

式（3.1.24）和式（3.1.25）含有变量xR及θd，同式（3.1.15）中第1式，或式（3.1.18）联立求解，就可得到在半约束期内导弹的扰动角θd及扰动角速度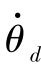、位移x及速度。若以滑离时间代入，则得到火箭的滑离参数。

半约束期定向钮载荷由式（3.1.17）确定，即

上述弹－装置系统在全约束期和半约束期的数学模型属于二阶常微分方程组，可以采用龙格库塔法用计算机求数值解。求解所得参数N1、N2等有关力和力矩的值可以为系统刚度、强度计算提供载荷。所得的导弹扰动角θd和扰动角速度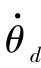等系统状态变量可用于判别初始扰动能否满足武器系统的要求，通过N1、N2、θd和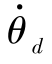的变化规律也可判别发射过程中系统是否产生了共振。

2）筒式垂直弹射的弹道导弹

筒式垂直弹射的弹道导弹如图3.5所示，弹－装置系统可分为发射筒、车和导弹3个刚体。导弹在全约束期具有一个移动自由度，在半约束期再加两个绕后定心部的转动自由度。发射筒具有一个垂直移动自由度和俯仰、偏航两个转动自由度。车体具有质心垂直移动和绕质心转动的自由度。每个自由度之间有等效弹簧和阻尼器相连，用于等效相关结构的综合刚度和阻尼。发射过程所受的动载荷根据“弹射”和“垂直”这两个发射特点参阅3.3节确定。

为了进一步提高分析精度，建立刚柔耦合模型有时是必要的。例如，将本小节中发射箱内的导轨视为连续弹性体，对精确地获得初始扰动值有时是有益的。又由于大型导弹发射车一般长度在10m以上，把车架视为连续弹性体也有利于提高精度，对于全刚性支承的发射装置更是如此。

由于发射过程中弹－装置系统为时变系统，使用通用的多体动力学分析软件（MBD）尚不能完全解决发射动力学分析问题。将通用软件和自行设计的软件交互使用，是分析计算发射动力学问题的最佳方法，可以极大地缩短建模和分析周期，提高分析计算的可靠性，扩大软件的通用性。当前广泛应用的多体动学分析软件有ADAMS、DADS、RecurDyn和SIMIPACK等。为了建立刚柔耦合多体动力学模型，可以将有限元分析软件（FEA）和多体动学分析软件交互使用。目前已应用的有限元分析软件有NASTRAN、ANSYS和ABAQUS等。燃气流载荷的计算可以采用FLUENT、CFX、STAR－CD等计算流体力学（Computational Fluid Dynamics，CFD）的分析软件和多体动力学分析软件交互使用。

对于机电控制系统或流体传动控制系统，将MATLAB、MATRIX和EASY 5等软件和MBD交互使用，可以分析计算控制因素对发射系统的综合影响。