航天器发射技术： 理想速度、宇宙速度与多级火箭

1.运载火箭的理想速度

运载火箭的理想速度公式是由俄国伟大的科学家齐奥尔科夫斯基所创立的。他基于运载火箭大都飞行在外大气层及其以上较高的高度，而认为对这种火箭的飞行可以忽略重力和气动力对火箭的作用。这样，运载火箭的飞行就完全是在火箭发动机推力的推动下完成的。在这种情况下，运载火箭所能达到的飞行速度称为理想速度。当然，它是大于实际速度的。

1）单级火箭的理想速度

火箭忽略重力和气动力的运动方程为

式中，P为推力，略去了推力成分中的压差推力部分；ue为火箭发动机的喷气速度。

将式（2.2.20）式变换为

积分上式得

式中，vI为理想速度；v0为起飞速度，从地面起飞时，v0＝0；m0为起飞质量；mk为发动机停火或推进剂燃烧结束时的火箭质量，有时也表示推进剂燃尽时的火箭净质量。

对于式（2.2.21），若令v0＝0，则变为

式（2.2.22）即著名的运载火箭理想速度公式。式中的mk／m0一般称作火箭的质量比，也可称为火箭的结构系数，因为它反映了火箭结构与所盛推进剂质量之间的关系。火箭的质量比一般用μk来表示，即μk＝mk／m0，显然，μk＜1。

将μk代入式（2.2.22），则得理想速度的另一种表达形式：

由于ue≈－ISPV，此处ISPV是火箭发动机的真空比冲，可得理想速度的又一种表达形式：

由式（2.2.22）～式（2.2.24）可看出，ue或ISPV越大，μk越小，则vI越大。

上述的理想速度公式主要适用于运载火箭，因为在大气层中，特别是在30 km高度以下飞行的飞行器，它的气动力和重力都是不可忽略的。若一定要忽略，则计得的理想速度误差会很大，实际参考价值也就不大了。

顺便提及，当火箭的运动速度接近光速时，计算理想速度则需利用相对论的原理，相应的公式是

式中，C为光速，C＝299 792.46 km／s；其余符号同前。

式（2.2.25）称为阿克莱公式，又称为广义齐奥尔科夫斯基公式，在恒星际航行中才会用到它。

2）多级火箭的理想速度

既然单级火箭的理想速度找到了计算公式，很容易设想，对于两级以上的火箭，可以套用单级火箭理想速度公式。如果先对第一级而言，公式中的ue就用第一级的，而m0用所有各级（含有效载荷）在一起时的起飞质量，mk则为起飞质量减去第一级已经烧掉的推进剂质量，这样求得的理想速度是第一级做出的贡献。当第一级的作用完成后将其扔掉。接着第二级点火，于是余下的级则在第一级已获速度（称v1）的基础上，仍按上述思路由第二级做出贡献获得它应有的理想速度（称v2），这时整个火箭的理想速度已达到v1＋v2。当然，第二级的作用完成后也将其扔掉。图2.15所示为三级火箭逐级加速逐级脱落示意。依此类推，直到末级做出贡献，就找到了多级火箭的理想速度，它是各级各自所获速度的总和。其表达式可以很容易地写出来：

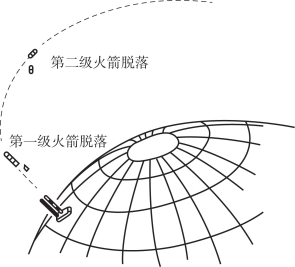
图2.15　三级火箭逐级加速逐级脱落示意

或

式中，vI为多级火箭的理想速度；uei为第i级的喷气速度；μki为第i级的质量比，即μki＝，此处m0i是第i级（其前的各级已脱落）的起飞质量（含i级以上各级和有效载荷），mki是m0i减去第i级的已燃推进剂质量；ISPVi为第i级的真空比冲。

如果所有各级的μe和μk都相同，则式（2.2.26）和式（2.2.27）可写为

或

式中，n为火箭级数。

2.宇宙速度与多级火箭

1）宇宙速度

从地球表面发射航天器，其环绕地球、脱离地球和飞出太阳系所需的最小速度，分别称为第一、第二和第三宇宙速度。这些速度的大小分别取决于航天器的轨道形状，即环绕地球的圆周轨道、脱离地球的抛物线轨道和飞出太阳系的双曲线轨道。因此，宇宙速度也被定义为，在引力场中，航天器进入上述几种轨道的临界速度值，并分别称为第一、第二和第三宇宙速度值。(www.xing528.com)

（1）第一宇宙速度（V1）。

人造地球卫星环绕地球表面作圆周运动，忽略大气作用，根据卫星所受的地球引力等于其离心力的条件即可求得第一宇宙速度，由

式中，m为卫星的质量；g0为地球表面的重力加速度；V1为第一宇宙速度；R为地球的平均半径。

可得

将g0＝0.009 81 km／s2和R＝6 371 km代入式（2.2.31），得

通常称第一宇宙速度为8 km／s，就是这样计算出来的。不过地球表面的空气密度很大，卫星是不能在这样的低空条件下环绕地球旋转的。一般都在几十或百千米以上的高空运行。离地球表面越远，环绕半径自然越大，但地球引力却小了，二者综合作用的结果是使环绕速度越来越小。图2.16所示为环绕速度随地球表面以上高度的变化。月球对地球的环绕速度只有1 km／s多一点，就是因为月球距地球38万km，而其所受到的地球引力却只有地球表面物体所受引力的1／3 600。表2.1所示为围绕地球最小运行速度与高度的关系。

要使卫星真正围绕地球作圆周运动是有条件的，一是V1＝8 km／s，二是V1的方向在入轨点恰好与地心线垂直，三是无摄动。只要有一个条件不满足，其运行轨迹都不会是真正的圆。前面的两个条件若在标准值附近摆动，所走出来的轨迹都将变成椭圆。

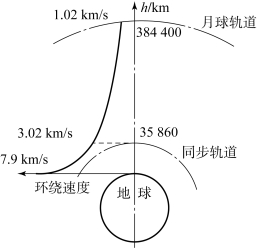
图2.16　环绕速度随地球表面以上高度的变化

表2.1　围绕地球最小运行速度与高度的关系

（2）第二宇宙速度（V2）。

所谓脱离地球意即脱离地球引力场之意。但对于第二宇宙速度来说，其第二层含义还有环绕太阳运行的意思。第二宇宙速度的计算涉及抛物线轨道的求解，此处直接给出计算结果，即V2＝＝11.2 km／s。第二宇宙速度因能使航天器沿抛物线轨道脱离地球，故也称为脱离速度、逃逸速度或抛物线速度。第二宇宙速度也随入轨的高度而变化，也是越高速度越小。例如，在地球表面附近，V2＝11.2 km／s，在200 km高空，V2＝11.01 km／s。假若除地球引力外，再没有其他力，具有V2速度的航天器将相对地球沿抛物线轨道运行，且离开地球多远都可以。但实际上，脱离地球引力场后，不能脱离太阳引力场。所以，沿抛物线轨道运行的航天器一般总要进入相对太阳的椭圆轨道，环绕太阳运行。

（3）第三宇宙速度（V3）。

航天器从地面附近发射能飞出太阳系的最小初始速度称为第三宇宙速度。它是这样确定的，当航天器达到地球引力作用范围边界（距地球约为93万km）时，应具有对应于太阳的第二宇宙速度，即太阳的脱离速度。但航天器毕竟是从地球上发射的，当从地球表面上发射航天器时，即使在充分利用地球公转速度（约30 km／s）的情况下，也得再获得相对于地球而言的16.6 km／s的速度，并沿双曲线轨道运行才能飞离太阳系并进入银河系。

航天器要飞离太阳，先要在地球上以V3的速度沿相对地球的双曲线轨道运行，飞离地球，所以，第三宇宙速度有时也称为双曲线速度。当航天器脱离了地球进入太阳引力场运行时，则沿着相对于太阳的抛物线轨道运行，最后再脱离太阳引力场而飞离太阳系。

宇宙速度的概念也适用于分析处在任何行星或其天然卫星以及太阳引力场中的航天器的运行。例如，在月球表面，第一宇宙速度为1.680 km／s，第二宇宙速度为2.375 km／s。而在金星和火星上，第二宇宙速度分别为10.4 km／s和5.0 km／s。

2）多级火箭

为了达到宇宙速度，按现阶段的火箭发动机技术水平和弹体结构设计水平来看，单级火箭都是无法实现的。考虑到当代较为先进的技术水平，若取火箭发动机喷气速度ue＝3 000 m／s，火箭质量比μk＝0.15，则单级火箭的理想速度为

连理想速度都达不到第一宇宙速度，何况实际速度呢？假若还取上述参数值，但设计成二级火箭，则其理想速度为

该速度看似已达到了第二宇宙速度，考虑到实际飞行中由于重力损失和气动力损失导致的速度损失为2 000～3 000 m／s，上述理想速度只可说是已经实际达到了第一宇宙速度。若采用三级火箭，则

该速度看似已达到第三宇宙速度，实际上也只能说达到第二宇宙速度是绰绰有余罢了。总之要想达到第二、第三宇宙速度，必须用多级火箭才能实现。

上述论证说明了多级火箭出现的必然性。其实还不限于此，某些洲际弹道导弹所需的速度远不及宇宙速度大，按说单级火箭是可以实现的，但考虑到总体技术的合理性，采用多级火箭为佳，这也促进了多级火箭的出现和发展。

多级火箭的总体组成方式有三大类——串联式、并联式、混联式，如图2.17所示。“土星V”多级火箭的分级、各级名称及结构组成示意如图2.18所示。

图2.17　多级火箭的总体组成示意

（a）串联式；（b）并联式；（c）混联式

图2.18　“土星V”多级火箭的分级、各级名称及结构组成示意

串联式、并联式和混联式多级火箭的优、缺点比较见表2.2。

表2.2　串联式、并联式和混联式多级火箭的优、缺点比较

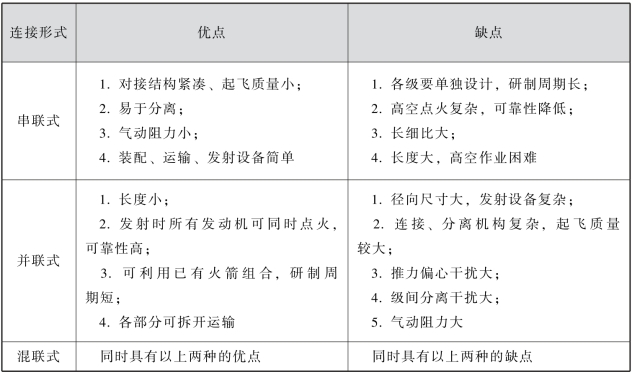
基于以上优、缺点的分析，弹道导弹一般采用串联式，这主要是便于运输、发射准备时间短、生存能力高等优点所决定的。运载火箭则多采用并联式或混联式，这是因为在非战条件下，它们的优点犹存，而某些缺点变得可以接受。