航天器发射技术：空气动力学基本知识

火箭、导弹在大气层内飞行总是受到空气动力的作用，本小节简要给出部分空气动力学的基本知识。

1.声速与马赫数

当物体在大气中发生振动时，就会对周围大气产生扰动，使大气压强和密度发生微小变化并以一定的速度向周围传播。这一传播速度称为声速，用a表示。声速与气体的温度T存在式（2.2.11）所示的关系：

式中，k为气体的比热比，对于空气k＝1.4；R为气体常数，对于空气R＝287.1 J／（kg·K）；T为气体的热力学温度（单位为K）。

对于空气，式（2.2.11）可表示为

在气温为15℃的海平面上，声速a＝340.3 m／s。

马赫数（Mach number）是指气体流动速度v（或飞行器的飞行速度）与当地声速a的比值，通常用Ma表示，

Ma＝v／a（2.2.13）

在同一个流场中，各个位置上的运动速度v可能不同，这样各点处的压强P、密度ρ、温度T也就不同，显然各处的声速a就不相同，自然马赫数也不相同。当气体流动的速度v为超声速（Ma＞1）和亚声速（Ma＜1）时，气体流动的特性有着本质上的不同。根据气体流动马赫数，把气体的流动分为下面几种状态：低速气流，此时Ma≤0.4；亚声速气流，此时0.4＜Ma≤0.75；跨声速气流，此时0.75＜Ma≤1.2；超声速气流，此时1.2＜Ma＜5；高超声速气流，此时Ma≥5。

2.附面层与气动加热

附面层就是附着在表面上的一层流体，其形成原因就在于流体有黏性。水泼到一块平板上，板面被沾上了一层水，就是因为水有黏性，贴近壁面的一层被滞止下来而流不动了，层外的水则继续向前流去。气体流经物体表面与水流相似，也有一层贴附在表面上不动，这是因为气体也有黏性。当然，气体的黏性一般比液体小得多。

图2.9所示为气流流经机翼翼面所产生的附面层。在机翼的前半部分上、下表面上均产生层流附面层，其中的流速剖面如上左圆圈中所示；在机翼的后半部分上、下表面上均产生紊流附面层，其中的流速剖面如上右圆圈中所示。

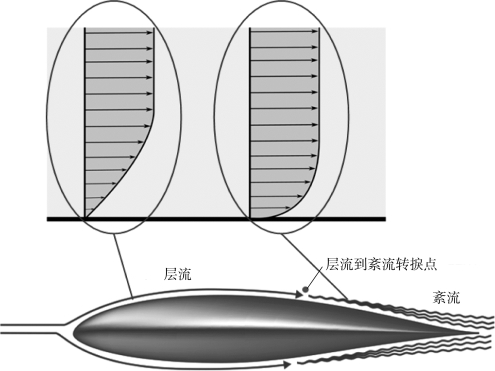
图2.9　层流附面层和紊流附面层

附面层的流态与气流的黏性系数μ、密度ρ、速度v以及被流经物体的特征长度L有关。雷诺（Reynolds）把这几个影响因素归结为雷诺数Re＝ρvL／μ。由层流转变为紊流的雷诺数称为临界雷诺数Ret，所以当Re小于Ret时，附面层的流态为层流，大于Ret时，则流态变为紊流。由试验得知，空气沿平板流动的Ret大约为105。

在层流附面层内，气体的流动呈分层流动状，各层间互不混淆，层内沿壁面法线方向的速度分布近似抛物线形状，在壁面处速度为零，在附面层边界处速度达到外部位流的速度；在紊流附面层内，各层气体微团除了向前运动外，还相互乱窜，因此称其为紊流（也称湍流），层内各点的速度随时间脉动，层内速度沿壁面法线的方向分布。在紊流附面层的底部，当不考虑存在层流底层时，其速度为零；当存在层流底层时，其速度应为底层界面上的速度。在紊流附面层的边界上，速度达到外部位流的速度。

下面介绍附面层理论的工程应用。第一个问题是附面层在气动计算上的应用。

附面层理论本身内容很多，也很复杂。但在飞行器作高速飞行的情况下，附面层实际上只是贴近壁面的一个极薄层，而且在它的边界上速度达到了外部位流的速度。这样一来，当Re很大时，黏性影响区很薄，相对于无黏流的绕流而言，速度因黏性而发生的变化都集中在这个很薄的影响区内，这时区内的法向速度梯度很大，但在这个区以外，法向速度梯度几乎为零，黏性作用可以忽略不计，即当作理想（无黏）流体看待。于是，气体黏性所起的作用可以认为只局限在附面层以内，一旦附面层边界求出，可以此为假想壁面来求解它的无黏流绕流问题。这当然使飞行器的气动计算问题得以大大简化，在工程上具有很大的实际意义。

第二个问题是飞行器的气动加热问题。所谓气动加热，实质上是指气流滞止或变慢时由气流能量的全部或部分转变为热能。高速气流的总能量由两部分组成，即动能和热焓。最常见的气动加热有两种，一种是气流被物体阻挡，流动的气体被完全滞止在物体的某前沿部位，这时气流的全部动能都被转化为热能而加在气流滞止的物体部位处。该部位所达到的温度可由高速气流的能量方程来求解，即

既然动能与热焓之和恒为常数，动能降低，热焓就增加，亦即温度增加。当流速降为零时，热焓值最大，此时所达到的温度最高，称为总温，也称为滞止温度，一般以T0表示：

式（2.2.16）就是常用的滞止温度（总温）计算公式。空气的k＝1.4，代入上式即得

假如导弹在5 km的高度上（该高度上的气温T＝255.65K）以Ma＝5的速度飞行，则在其某些前端部位的中心点上出现的总温值可达到T0＝1 261℃。这时，为飞行器的结构着想，就要关注气动加热问题。

以上是气动加热的一种情况，下面介绍附面层的存在所引起的气动加热问题。

附面层的存在是由于气体的黏性，黏性导致气体与壁面之间的摩擦，而且由于存在速度梯度，在流层之间也存在摩擦，不管在层流附面层还是紊流附面层中，摩擦都一样存在。有摩擦就会生热，这种热实质上还是由动能的降低转换过来的，这为分析提供了方便。在第一种情况中，速度完全被滞止时的温升，已给出了计算公式（2.2.16）。对附面层的情况除紧贴壁面、速度滞止为零外，稍远，速度虽降低但不为零，而且在附面层边界上速度恢复为外部位流的速度，于是，相应于速度剖面出现了一个温度剖面，一般称它为温度附面层。温度附面层的最底层速度滞止为零，但底层以上速度不为零，而且一般速度梯度较大。这时就不能处于滞止状态，因此也不能完全用式（2.2.16）计算其温度，但对于底层附近的极薄层内，因其极近于滞止状态，故仍用式（2.2.16）加一项修正系数计算其温度，通常称该温度为恢复温度，其表达式为

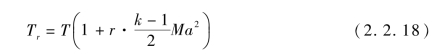
式中，Tr为恢复温度，即紧贴壁面的气体温度；r为温度恢复系数，其值与普朗特数Pr有关。

当Pr＝1时，r＝1，这时恢复温度等于滞止温度。对于层流附面层可取r＝0.845，对于紊流附面层可取r＝0.88。

Tr值对一定的附面层是个定值，但实际附面层底层的温度却与壁面的热状态有关。如果壁面是绝热的，Tr就是壁面温度；如果壁面是冷的，则壁面温度要小于Tr；如果壁面是热的，则壁面温度要大于Tr。

在存在附面层的情况下，所谓壁面的气动加热是附面层的恢复温度高于壁面温度，从而要向壁面内部传热所致。当达到热平衡状态时，壁面的温度即气动加热的温度，这时可用式（2.2.18）计算。

由于气动加热的存在，在设计火箭、导弹，尤其是返回式卫星和再入弹头时，必须考虑壁面的受热问题。

3.气动力和气动力矩(www.xing528.com)

1）常用坐标系

选用按右手定则确定的笛卡儿坐标系。

（1）弹体坐标系Ox1 y1 z1。

该坐标系的原点O选在导弹的质心上，Ox1轴取在导弹的纵轴上，指向导弹的头部为正；Oy1轴取在导弹的纵向对称面内，指向上方为正；Oz1轴的位置和正指向按右手定则确定，如图2.10（a）所示。

（2）速度坐标系Ox2 y2 z2。

速度坐标系Ox2 y2 z2的原点O取在导弹的质心上；Ox2轴与导弹质心运动矢量重合，Oy2轴在导弹纵向对称面内，垂直于Ox2轴；Oz2轴按右手定则确定，如图2.10（b）所示。

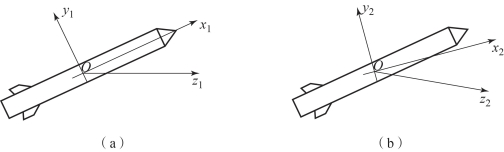
图2.10　弹体和速度坐标系

（a）弹体坐标系；（b）速度坐标系

（3）攻角α和侧滑角β的定义。

攻角α为导弹质心运动的速度矢量v在导弹纵向对称平面的投影v′与导弹弹体坐标系中Ox1轴之间的夹角。正的攻角沿Oy1轴产生正的升力。

侧滑角β为速度矢量v与导弹纵轴对称平面之间的夹角，正的侧滑角产生负的侧向力（此时的侧向力与Oz1轴的正方向相反）。

攻角和侧滑角示意如图2.11所示。

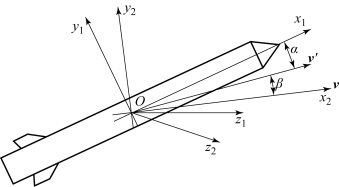
图2.11　攻角和侧滑角示意

2）气动力

当导弹以一定的速度在大气中运动时，导弹各部分（如翼面、舵面等）都会受到气动力的作用，这些气动力的总和，就是导弹的总气动力F。可将F向任意方向进行分解，F在导弹的对称平面内并垂直于速度矢量v的分量就是升力FL，而F在顺气流速度矢量v方向的分量就是阻力FD，如图2.12（a）所示。气动力产生的原理大致可以分为压力差和摩擦两大类。下面根据压力差和摩擦两方面的原因讨论升力和阻力产生的原因。

（1）升力。

这里以低速理想流为例来解释翼面由压力差产生升力的物理原因。图2.12（b）为气流以一定攻角流过对称翼型的流线图。

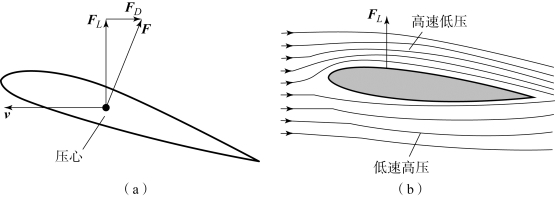
图2.12　气动力及升力示意

（a）气动力示意；（b）升力示意

流线是指空气微团流动的路线，流线之间的气体微团不会串流。因此流线好似无形的管壁，两条流线之间的气流像在管道中流动一样，称为流管。把对称翼型以一定角度放在气流中，气流经翼面的前缘，分成上、下两股沿着翼面的上、下表面流动，而在翼面的后缘处重新汇合向后流去。这样在上、下翼面附近的流管就变得不一样了，上表面的流管比下表面的流管细。由质量方程和伯努利方程可知，上表面的流速比下表面的流速快，上表面的压强比下表面的压强小，于是翼面上、下表面的压强不相等，自然就产生升力FL。

在舵面等部件上产生升力的原因，与翼面产生升力的原因类似。

（2）阻力。

阻力按其产生的原因可分为摩擦阻力、压差阻力、诱导阻力。

①摩擦阻力。摩擦阻力是由大气的黏性产生的。因为有黏性的大气流过导弹表面时，紧贴导弹表面的一层气体速度为零，从导弹表面向外，气流速度才一层比一层加大。气流速度之所以越贴近导弹表面越慢，是由于空气流动受到导弹表面摩擦作用的结果。根据作用和反作用定律，被减慢的空气必然给予导弹表面与飞行方向相反的作用力，这就是摩擦阻力。摩擦阻力不论在低速飞行和超声速飞行时都是存在的。

②压差阻力。空气流过翼面时，在翼面前缘部分受翼面阻挡，流速减慢，压强增大；在翼面后缘，由于气流分离形成涡流区，压强减小。这样翼面前、后便产生压强差，形成阻力。这种由前、后压强差形成的阻力叫作压差阻力。舵面、机身等部件也会产生压差阻力。如果导弹以超声速飞行，还会产生激波阻力，激波阻力实际上是压差阻力的一种。

③诱导阻力。诱导阻力是伴随升力而产生的，如界没有升力，诱导阻力也就等于零。这个由升力“诱导”而产生的阻力，称为诱导阻力。

导弹的诱导阻力主要来自翼面。当翼面有升力时，下表面的压强比上表面的大，下表面的气团力图绕过翼尖流向上表面。这样翼尖部分的气体就发生扭转而形成翼尖涡流。翼尖涡流使流过翼面的大气产生下洗速度，使速度向下倾斜形成下洗流。由下洗流所产生的升力R垂直于下洗流流动方向。R可以分解为垂直于导弹运动方向的分力Y和平行于导弹运动方向的分力X。Y依然起着升力的作用，但是X则起着阻力的作用。这个附加阻力就是诱导阻力，诱导阻力随攻角的增大而增大。

3）气动力矩

作用于导弹上的气动力作用点如不通过导弹的质心，就会产生绕质心的力矩，如图2.13所示。这一力矩可以分解为绕弹体坐标系的3个轴的力矩。绕Oz1轴的力矩称为俯仰力矩Mz，也称为纵向力矩。绕Oy1轴的力矩称为航向力矩，也称为偏航力矩My。绕Ox1轴的力矩称为滚动力矩Mx，也称为倾斜力矩。力矩的方向与对应轴的正方向一致时则为正力矩。

图2.13　气动力矩示意

关于气动力矩，建议读者参考相关空气动力学教材，限于篇幅，此处不再详述。