航天器喷气推进原理-航天器发射技术

1.推力的产生

火箭发动机喷气推进的原理与放开口的充气气球运动的原理是相同的，如图2.7（a）和（b）所示。如果将一个气球充气并扎上口，气球内的压强仅比环境压强略高，因为气球内压强在所有方向上相等，所以气球在任意方向上合力均为零，处于平衡状态，如图2.7（c）左上图所示。如果打开气球的开口，此时开口就像一个洞，在此处没有可供内部压强作用的表面积，所以气球上合力不再为零，即产生了推力，气球在推力的作用下向前飞行，如图2.7（c）右上图所示。火箭和气球产生推力的原理是非常相似的，唯一显著的区别是高压气体的产生方式，在火箭中，气体是通过燃烧固体或液体推进剂产生的，如图2.7（c）下图所示。

考虑图2.8（a）所示的火箭发动机，当推进剂在燃烧室里燃烧时，由于剧烈的化学反应，产生大量的燃气，它们受燃烧室壁的限制，扩展不出去，向后又受喷管的限制，流通不畅，因此只好增压来收容大量气体，这就是燃烧室壁上作用有很高压力的原因。这些压力作用到室前壁上自然会形成一个推动火箭前进的力，此力使火箭以速度v前进。但这是有条件的，即当火箭发动机装有尾喷管的时候才能高效地完成。假若燃烧室是密闭的，燃气憋在里面，压力再高也无用，因为在各个方向上都平衡掉了，就像图2.7（c）左上图所示的气球一样，而且压力太高了可能炸裂燃烧室壁。但当向后有开口时，例如只开一个一般的圆孔，情况就会改观，经过圆孔就能喷出气体，而且火箭也能得到一定的推力，但这样做，其推进效率不高。如果紧接燃烧室向后装上一个如图2.8所示的尾喷管（先收缩，后扩张，即拉瓦尔喷管），情况就大不一样了。燃烧室内的燃气压强增高后，燃烧室壁就压迫着燃气向喷管方向流动，把大量的燃气经喉部、扩张段和喷口，以超声速乃至几倍声速的高速度ve喷射出去。在这种情况下，高喷气速度换来大推力，这时的推进效率是高的。

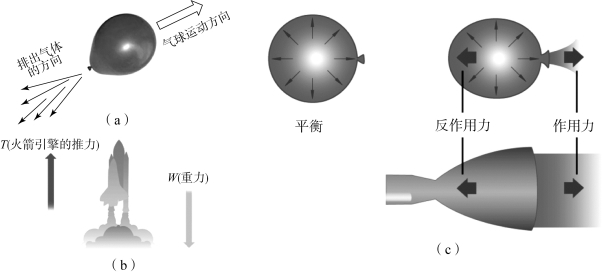
图2.7　喷气推进原理示意

（a）气球；（b）火箭；（c）喷气推进原理

图2.8　火箭发动机推力产生示意

在上述过程中，燃烧室壁对燃气的压力就形成了燃气向喷口方向的流动并从喷口喷射出去，这时也可以说燃气从燃烧室的压强那里获得了一部分动能，但反过来说，燃气对燃烧室壁的反作用压力的合力就形成了推动火箭发动机前进的动力，即推力。假若把燃烧室壁对燃气的压迫称为作用力，那么燃气对燃烧室壁的反抗就称为反作用力。这就是利用反作用原理产生推力的道理，实际上也就是“喷气”产生推力，或者说“喷气”就能“推进”的道理。

2.推力的计算

下面推导火箭发动机在非理想工作状态下的推力计算公式，推导过程将基于图2.8进行。

图2.8（a）中Pi为燃烧室内的压强，在实际应用中其在燃烧室的不同位置可能是不同的，这里假设其在燃烧室内处处相等；Pa为环境压强，这里认为其是常数；Pe为喷管出口平面上的压强，取出口平面的平均压强；Ae为喷管出口的面积。

图2.8（a）中顶部和侧面的箭头表示作用在火箭发动机内部和外部的气体压强，底部的箭头表示在出口平面上作用于排出燃气的压强。本小节的分析将忽略重力和空气阻力的影响。

接下来，仅考虑火箭发动机内的推进剂（含燃气，此后提及推进剂均含燃气），这样可以充分考虑火箭发动机壁和推进剂之间的作用力，这种作用力与火箭的推力有关。图2.8（b）显示了推进剂，沿顶部和侧面的虚线表示火箭发动机内壁和推进剂之间的接触界面，沿底部的虚线表示燃气的出口平面，压强Pe作用在该平面上。图中，Fw是由于与火箭发动机内壁接触而施加在推进剂上的向下合力（用沿顶部和侧面的虚线表示）。该力的计算方法是：（1）将内壁某点的局部压强Pi乘以壁面上的微分面积；（2）使用微积分法，对整个内壁面进行积分以求得合力；（3）确定该力的垂直分量（Fw）。此处不显示此计算的详细信息。需要注意的是，由于火箭发动机的几何对称性，合力仅作用在垂直方向，而没有侧向分量。

这里，定义向上的力为正，向下的力为负，将作用在推进剂上的力相加，并应用牛顿第二定律可得

式中，mp为发动机内的推进剂的质量；a为发动机的加速度；u为燃气相对于火箭的速度，近似为常数；dmp／dt为推进剂燃烧速度。(www.xing528.com)

接下来来分析图2.8（c）所示的火箭发动机的受力，图中Frb为火箭箭体作用在火箭发动机上的力。将作用在火箭发动机上的所有力相加，并应用牛顿第二定律可得

式中，mre为火箭发动机的质量；Pa Ae为环境压强作用在发动机出口的力。

根据牛顿第三定律，作用在火箭箭体的力Frb是指向上（为正）的，根据牛顿第二定律可得

式中，mrb为火箭箭体的质量，不含火箭发动机及其内的推进剂。

结合式（2.2.5）和式（2.2.6）可得

结合式（2.2.4）和式（2.2.7）可得

式中，（mp＋mre＋mrb）为任意时刻火箭的总质量，根据牛顿第二定律，式（2.2.8）的左侧即作用在火箭上的推力，可表示为

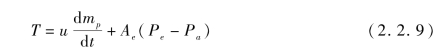
式（2.2.9）就是计算推力的一般方程，式（2.2.9）右侧第一项为动量推力项，第二项是由喷管出口压强和环境压强之间的差异所产生的压强推力项。当火箭发动机处于理想工作状态，即喷管出口压强Pe等于环境压强Pa时，压强推力项变为零，式（2.2.9）变为

此时，燃气射流流出喷口后既不膨胀也不压缩，喷管推力达到最大值。相对于动量推力项，压强推力项总是小量，因此在精度要求不高的分析场景中可以忽略。

本小节中的分析基本上是力和动量分析，要作一个完整的推力分析，必须使用热力学和流体力学知识研究燃气在喷管中的膨胀过程，这样的分析（此处未给出）能够优化发动机设计和喷管几何结构，以使发动机在工作期间实现或尽可能接近最佳膨胀。这部分知识将在第三章“气体射流动力学”部分给出。