航天器发射技术: 火箭和导弹的运动原理

火箭、导弹（此后简称为火箭）在运动过程中，不断有发动机的燃烧产物（燃气）向后喷射，这一方面使火箭得到了向前的推力，另一方面火箭本身的质量不断在减小。这样一种运动过程不同于一般定质量物体受外力作用的运动过程，一般被称为变质量物体运动方程。本小节以火箭运动为例，推导变质量物体运动方程。该方程的推导方法不一，本书引进一种直观、易懂、简明的方法。

如图2.6所示，火箭在作直线运动。在t时刻，火箭的质量为m；在t＋dt时刻，喷出燃气Δm，将火箭加燃气设为时刻t＋dt感兴趣的系统如图2.6（b）所示，这时，系统的总质量仍为m。这样，对系统的运动而言，仍可视为定质量系统的运动，所以可以将动量定理运用于该系统，导出火箭的变质量运动方程。

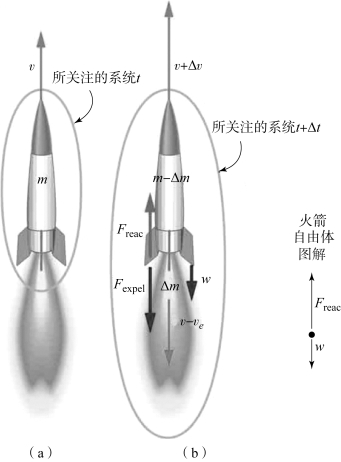
图2.6　火箭直线运动示意

根据动量定理，在任一时刻，系统的动量变化等于该时刻外力作用在系统上的冲量。

设在任一时刻t，系统的质量为m，速度为v。在t＋dt时刻，系统的质量分为两部分，火箭为（m－dt），燃气为dt，但其总合仍为t时刻的系统质量m。其中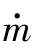为单位时间的燃气质量流量＝－dm／dt，负号表示质量在减小。

与上述两部分质量相对应的速度为

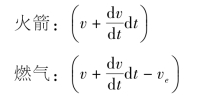(www.xing528.com)

式中，ve为喷气速度，方向与v相反。

dt时间内系统的动量定理关系式为

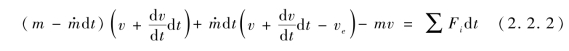
式中，Fi为作用于系统的元力。

变换式（2.2.2）可得

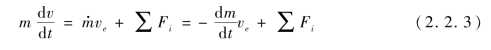
式（2.2.3）即火箭（变质量物体）的运动方程。它与定质量物体运动方程相比，多了（－dm·ve／dt）一项，其物理意义即燃气的动量变化率，即动量除以时间，实际上即喷气的反作用力——火箭推动力。

若dm／dt＝0，则式（2.2.3）可化为定质量物体运动方程，即牛顿第二定律。