本讲中的许多问题牵涉到直线与圆锥曲线的关系问题,这是解析几何综合题求解过程中经常碰到的重大知识点汇集得最多最为紧密的地方,在数学上任何一个知识点都有其生成与发展以至应用的过程,它们绝对不是独立的概念,必然与其他知识点有着密切的联系,构成一串串的知识链,所以许多数学知识要联系起来看,直线与曲线的位置关系以及由此引出的探索性与新颖性问题正是需要集合众多的知识与方法才能攻克的题型.
以解析几何为背景的探索性与新颖性问题研究的核心仍然是直线与圆锥曲线的关系问题,在题目的设计上布置了一个新的场景,探索性问题大部分是存在判断型.新颖性问题则在研究型上做文章,所以攻克这类高考热点题型,主要应抓住以下几点.
(1)直线与圆锥曲线的相对位置关系,如交点个数问题,仅通过方程组解的状况来判断是不够的,如椭圆是一条光滑的封闭曲线,可以类似于直线与圆的位置关系加以研究(用判别式),双曲线与抛物线都不是封闭曲线,当直线与双曲线的渐近线平行或与抛物线的对称轴平行时,直线与曲线仅有一个公共点,并不仅是方程组求解时Δ=0的情景,圆锥曲线与圆锥曲线的关系问题更要结合图形及相关性质加以分析.
(2)研究直线被圆锥曲线所截弦的问题,消元后若求弦长,则常用韦达定理和弦长公式![]() 或
或![]() 若运用直线的参数方程,则利用参数方程中参数t的几何意义:L=|t1-t2|,求弦上某点的坐标,则常用韦达定理和定比分点公式、中点坐标公式,可见韦达定理在解析几何中的应用非常重要,若牵涉到参变量,则参变量的取值范围不容忽视.
若运用直线的参数方程,则利用参数方程中参数t的几何意义:L=|t1-t2|,求弦上某点的坐标,则常用韦达定理和定比分点公式、中点坐标公式,可见韦达定理在解析几何中的应用非常重要,若牵涉到参变量,则参变量的取值范围不容忽视.
(3)关于直线与圆锥曲线关系中点的对称问题,如曲线上两点关于已知直线对称,求某参变量的取值范围,必须紧紧抓住垂直、平分两个方面并结合两个对称点的存在性.
解析几何探索性与新颖性问题的解答常常是代数的方法与几何图形的分析结合在一起,有时还要与函数、导数、不等式、三角函数、数列、向量等知识相交汇,此类题型的解法“奇伟”“瑰丽”,从中时时会显露出数学之美.解题时应当好好揣摩题意,并想方设法作进一步探讨,若不敢越雷池一步,势必会束缚人的才智,也不利于创新思维的开发与创新精神的培养.
下面介绍的就是近几年中出现的各类好题,仔细研读它们,你会发现以解析几何为背景的探索性、新颖性与研究性问题粗一看总是“山穷水复疑无路”,一旦领悟,找到了攻克的方向,就会出现“柳暗花明又一村”了.
一、例题精讲
例1 已知椭圆![]() 的离心率
的离心率![]() 且椭圆C上的点到点T(3,0)的最大距离为4,若P(x0,y0)在椭圆C上,则
且椭圆C上的点到点T(3,0)的最大距离为4,若P(x0,y0)在椭圆C上,则![]() 称为点P的一个“和谐点”,直线l与椭圆交于A、B两点,A、B两点的“和谐点”分别为M、N,已知以M、N为直径的圆经过坐标原点.
称为点P的一个“和谐点”,直线l与椭圆交于A、B两点,A、B两点的“和谐点”分别为M、N,已知以M、N为直径的圆经过坐标原点.
(1)求椭圆C的方程;
(2)△AOB的面积是否为定值?若为定值,试求出该定值;若不是定值,请说明理由.
解题策略 本题给出了“和谐点”的新情景,所谓“和谐点”的本质是点(坐标轴)的伸缩变换,解决的方法是相关点法.△OMN是直角边长为1的等腰直角三角形.若其面积为定值,能否具有运动变化中的不变性?而△AOB与△OMN等高,问题就转化为只需探求底边的关系,应借助平面几何知识推证.另外,涉及坐标的三角形面积公式为:在△ABC中,![]() 则△ABC的面积为
则△ABC的面积为![]() 此结论与2015年高考数学上海卷理科第21题类同,读者可以参阅下面的例2第(1)问,利用离心率建立a,b的关系,消元后根据有界性利用最大距离为4得到b,再确定a,从而求得椭圆C的方程.第(2)问,建构M、N与△AOB的面积关系为解题的关键,在用坐标法研究几何问题时,应充分利用几何图形的性质简化运算过程.
此结论与2015年高考数学上海卷理科第21题类同,读者可以参阅下面的例2第(1)问,利用离心率建立a,b的关系,消元后根据有界性利用最大距离为4得到b,再确定a,从而求得椭圆C的方程.第(2)问,建构M、N与△AOB的面积关系为解题的关键,在用坐标法研究几何问题时,应充分利用几何图形的性质简化运算过程.
解:(1)由题意得![]() 故a=2b.
故a=2b.
椭圆C的方程可设为4x2+y2=4b2(b>0).
设R(x,y)是椭圆C上的任意一点,其到T点距离的平方为
|RT|2=(x-3)2+y2=x2-6x+9+y2=x2-6x+9+4b2-4x2
=-3x2-6x+9+4b2=-3(x+1)2+12+4b2,x∈[-b,b].
若0<b<1,当x=-b时,|RT|2取得最大值(b+3)2,即(b+3)2=16.
解得b=1(舍去);
若b≥1,当x=-1时,|RT|2取得最大值12+4b2,即12+4b2=16.
解得b=1,a=2.
故椭圆C的方程为![]()
(2)设A(x1,y1),B(x2,y2),则![]()
1当直线AB的斜率不存在时,即x1=x2,y1=-y2,
由以MN为直径的圆经过坐标原点可得OM⊥ON,即
![]() 即
即![]()
又点A(x1,y1)在椭圆上,![]() 解得
解得![]()
2当直线AB的斜率存在时,设其方程为y=kx+m.
由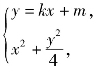 消去y得(4+k2)x2+2kmx+m2-4=0.
消去y得(4+k2)x2+2kmx+m2-4=0.
由根与系数的关系可得![]()
由以MN为直径的圆经过坐标原点可得OM⊥ON,
从而有![]() 即4x1x2+y1y2=0.
即4x1x2+y1y2=0.
故4x1x2+(kx1+m)(kx2+m)=(4+k2)x1x2+km(x1+x2)+m2=0.
将x1x2,x1+x2之值代入,整理得2m2-k2-4=0,∴k2+4=2m2.
而![]()
故![]() 而点O到直线AB的距离
而点O到直线AB的距离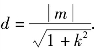
∴S△AOB![]()
综合 12 可知,△AOB的面积为定值1.
例2 (2015年高考数学上海卷理科第21题)
已知椭圆x2+2y2=1,过原点的两条直线l1和l2分别与椭圆交于A、B和C、D,记得到的平行四边形ABCD的面积为S.
(1)设A(x1,y1)、C(x2,y2),用A、C的坐标表示点C到直线l1的距离,请证明:S=2|x1y2-x2y1|;
(2)设l1与l2的斜率之积为![]() 求面积S的值.
求面积S的值.
解题策略 本题以直线与椭圆的位置关系为考查对象,涉及证明与求值.第(1)问的证明实质是推导用坐标表示的平行四边形的面积公式.读者可以从中归纳出三角形面积如何用坐标表示,虽然这是常规题,但能力立意突出,切入点也较多,可以有不同的证法与解法.
解:(1)证法一 依题意,直线l1的方程为![]()
点C到直线l1的距离为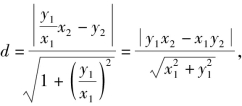
又![]()
∴S=|AB|·d=2|x1y2-x2y1|.
证法二 由题意知S=4S△AOC,且![]() (https://www.xing528.com)
(https://www.xing528.com)
故S=2|x1y2-x2y1|.
(2)解法一 设直线l1的斜率为k,则直线l2的斜率为![]()
直线l1的方程为y=kx,由![]() 得
得![]()
不妨设![]() 由对称性得
由对称性得![]()
同理可得![]() 因此
因此![]()
解法二 将A(x1,y1)、C(x2,y2)代入x2+2y2=1,得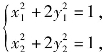
两式相乘,得![]() 展开得
展开得
即(x1x2+2y1y2)2+2(x1y2-x2y1)2=1. ①
而l1与l2的斜率之积为![]() 故有
故有![]() 即x1x2+2y1y2=0,
即x1x2+2y1y2=0,
代入①式得2(x1y2-x2y1)2=1,即![]()
∴S=2|x1y2-x2y1|![]()
解法三 椭圆x2+2y2=1 可化为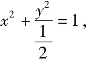
参数方程为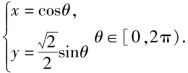
设![]() 则
则
整理得cosθ1cosθ2+sinθ1sinθ2=0,即cos(θ1-θ2)=0.
由(1)知S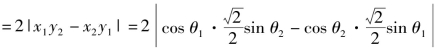
例3 已知椭圆Γ的方程为![]() 点P的坐标为(-a,b).
点P的坐标为(-a,b).
(1)若直角坐标平面上的点M、A(0,-b)、B(a,0)满足![]() 求点M的坐标;
求点M的坐标;
(2)设直线l1:y=k1x+p交椭圆Γ于C、D两点,交直线l2:y=k2x于点E,若![]() 证明:E为CD的中点;
证明:E为CD的中点;
(3)对于椭圆Γ上的点Q(acosθ,bsinθ)(0<θ<π),如果椭圆Γ上存在不同的两点P1,P2使得![]() 写出求作点P1、P2的步骤,并求出使P1、P2存在的θ的取值范围;
写出求作点P1、P2的步骤,并求出使P1、P2存在的θ的取值范围;
(4)设点P在椭圆Γ内且不在x轴上,如何构作过PQ中点F的直线l,使得l与椭圆Γ的两个交点P1、P2满足![]() 令a=10,b=5,点P的坐标是(-8,-1),若椭圆Γ上的点P1、P2满足
令a=10,b=5,点P的坐标是(-8,-1),若椭圆Γ上的点P1、P2满足![]() 求点P1、P2的坐标.
求点P1、P2的坐标.
解题策略 本例以直线与圆锥曲线的关系为载体,并把平面向量、解析几何、三角知识综合起来,考查向量的运算.直线与圆锥曲线关系中弦、弦的中点、点与曲线的位置关系、三角恒等变形、三角不等式等众多的基础知识与解题技能,考查多个方面的数学核心素养.通常我们讲以解析几何为背景的探索性与新颖性问题,有一类题型涉及新定义、新概念、新场景,其实“新”并非一定“难”,理解了条件中的“新”,化“新”为“旧”不难解决,另一类题型涉及多方面的数学知识,探究的问题一大堆且各不相同,这才是高难度的探索性与新颖性问题.比如本题集计算、证明、作图、探究于一体,烟雾重重,难度较大,这类题的求解既要宏观把握,又要落实细节,偶翻钱锺书《宋诗选注》,深受启发.解数学难题好比人入山水之间,景色千变万化,险景常临眼前,仿佛是郑獬诗所描写:“前树未回疑路断,后山才转便云遮”,通过思考解决难题其意境正如王安石诗:“青山缭绕疑无路,忽见千帆隐映来”“一水护田将绿绕,两山排闼送青来”,陆游诗:“山重水复疑无路,柳暗花明又一村”,刘攽诗:“一雨池塘水面平,淡磨明镜照檐楹.东风忽起垂杨舞,更作荷心万点声”,这些诗句都写得无比贴切生动,这岂不正是解数学难题的心路历程?
解:(1)设点M的坐标为![]()
于是,点M的坐标为![]()
(2)证明 由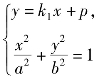 得(b2+a2k12)x2+2a2k1px+a2p2-a2b2=0.
得(b2+a2k12)x2+2a2k1px+a2p2-a2b2=0.
∴CD中点坐标为![]()
由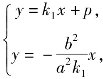 得l1与l2的交点E的坐标为
得l1与l2的交点E的坐标为![]()
由同一法,可知l1与l2的交点E为CD的中点.
(3)第一步:取PQ的中点![]()
第二步:过点R作斜率为![]() 的直线交Γ于P1,P2两点.
的直线交Γ于P1,P2两点.
由(2)可知,R是P1P2的中点,则PP1QP2是平行四边形,有![]() 要使P1,P2存在,则点
要使P1,P2存在,则点![]() 必须在椭圆内.
必须在椭圆内.
将![]() 代入椭圆Γ的方程,得
代入椭圆Γ的方程,得![]()
当且仅当![]() 时,点R在椭圆内.
时,点R在椭圆内.
整理得,(1+sinθ)2+(cosθ-1)2<4,即2sinθ-2cosθ<1,亦即![]()
又![]()
(4)设OF的斜率为k1,过F作斜率为![]() 的直线交椭圆于P1,P2两点.
的直线交椭圆于P1,P2两点.
由(2)可知,F是P1P2的中点,四边形PP1QP2是平行四边形.
![]() 直线P1P2即为所求.
直线P1P2即为所求.
由a=10,b=5及点P(8,-1),得PQ的中点为![]() 的斜率
的斜率![]()
过点S且斜率![]() 的直线方程是
的直线方程是![]()
记l与Γ的交点为P1,P2,则![]() 由
由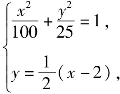
解得P1(8,3)、P2(-6,-4).
二、发散训练
1. 从椭圆![]() 上的动点M作圆x2+y2=b2的两条切线,切点为P和Q,直线PQ与x轴和y轴的交点分别为E和F,求△EOF面积的最小值.
上的动点M作圆x2+y2=b2的两条切线,切点为P和Q,直线PQ与x轴和y轴的交点分别为E和F,求△EOF面积的最小值.
2. 设抛物线y2=2px(p>0)的焦点是F,A、B是抛物线上互异的两点,直线AB与x轴不垂直,线段AB的垂直平分线交x轴于点D(a,0),记m=|AF|+|BF|.
(1)证明:a是p与m的等差中项;
(2)设m=3p,直线l∥y轴,且l被以AD为直径的动圆截得的弦长恒为定值,求直线l的方程.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




