解析几何必备技巧，轨迹探求方法详解

轨迹探求是解析几何的基本题型，其实质就是建立起动点坐标之间的解析关系式，常用的方法有：①直接法；②转移法；③定义法；④参数法；⑤交轨法；⑥向量法等.

轨迹探求的关键在于对坐标系、方程形式、参数的选择，在运用参数法并进行消参时，要注意运用代数变换的技巧和等价性问题，确定轨迹的范围是轨迹题中的难点.

本讲就轨迹探求的方法和必须注意的问题加以展开，同时介绍一些与轨迹探求相关的综合题.近年来求轨迹或轨迹方程的考查常常安排在解析几何综合题中的一道小题，在求出轨迹或轨迹方程后进一步研究与之相关的种种问题，如果说前面这部分没有做出来，后续问题的解答就无从谈起，一道综合题的得分可想而知.

一、例题精讲

例1　已知椭圆的两个焦点分别为F1(-1,0)、F2(1，0)，且椭圆C经过点设过点A(0，2)的直线l与椭圆C交于M、N两点，点Q是线段MN上的点，且求点Q的轨迹方程.

解题策略　直接法是求轨迹方程的通常方法，一般利用题目所给条件或常见动点轨迹的概念把动点坐标直接代入条件求出轨迹方程，当然对运算能力这一核心素养的要求很高，而且本题求x、y取值范围非常重要，是难点也是关键点，同时也考查了数形结合、转化与化归、分类与整合等数学思想以及思维的严谨性.

解：由椭圆定义知2a=|PF1|+|PF2|

又由已知c=1，∴b2=a2-c2=1.椭圆C的方程为

设点Q的坐标为(x，y)，

当直线l与x轴垂直时，直线l与椭圆C交于(0，1)、(0，-1)两点，

此时点Q的坐标为

当直线l与x轴不垂直时，设直线l的方程为y=kx+2.

∵M,N在直线l上，可设点M,N的坐标分别为(x1，kx1+2)，(x2，kx2+2)，则又|AQ|2=x2+(y-2)2=|1+k2|x2，由得

即　①

将y=kx+2代入中，得(2k2+1)x2+8kx+6=0.　②

由Δ=(8k)2-4×(2k2+1)×6>0，得

由②可知，代入①中并化简,得　③

∵点Q在直线y=kx+2上，代入③中并化简,得10(y-2)2-3x2=18.

由③及可知即

又满足10(y-2)2-3x2=18，故

由题意,Q(x,y)在椭圆C内，∴-1≤y≤1.

又由10(y-2)2=18+3x2，有且-1≤y≤1，则

∴点Q的轨迹方程为10(y-2)2-3x2=18，

其中

例2　已知椭圆的一个焦点为离心率为

(1)求椭圆C的标准方程；

(2)若动点P(x0,y0)为椭圆外一点，且过点P作椭圆C的两条切线相互垂直，求点P的轨迹方程.

解题策略　本题解答的关键是动静转换与整体代换，点P是两条切线的交点(定点)又是所求轨迹上的动点，两切线的关系是相互垂直，把一条直线的斜率k换成可以减少运算量；利用相切的条件由Δ=0得关于k与的一元二次方程，利用根与系数的关系及可求得动点P的轨迹方程，这是常规解法，还可以有其他解法，如结合向量来解，由PA⊥PB得又如利用椭圆的参数方程解可以减少运算量，倘若借助柯西不等式则是一种奇妙的解法.

解：(1)依题意得，因此a=3,b2=a2-c2=4.

故椭圆C的标准方程是

(2)解法一　设两切线为ll、l2.

1当l1⊥x轴或l1∥x轴时，对应l2∥x轴或l2⊥x轴，可知P(±3,±2).

2当l1与x轴不垂直且不平行时，x0≠±3，设l1的斜率为k.则k≠0，l2的斜率为

由上可得l1的方程为y-y0=k(x-x0)，其与椭圆方程联立，

消去y得(9k2+4)x2+18(y0-kx0)kx+9(y0-kx0)2-36=0.

∵直线l1与椭圆C相切，∴Δ=0，得

9(y0-kx0)2k2-(9k2+4)[(y0-kx0)2-4]=0，(www.xing528.com)

即

∴k是方程的一个根，

同理，是方程的另一个根.

由韦达定理得从而得其中x0≠±3.

∴点P的轨迹方程为

∵P(±3，±2)满足上式，∴点P的轨迹方程为

因此动点P的轨迹方程是x2+y2=13.

解法二　(向量法)过点P(x0，y0)作椭圆C的两条切线，设切点分别为A(x1，y1)、B(x2，y2)，则直线AB的方程为

当x0y0≠0时，由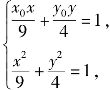 消去y得

于是

同理

且

　①

将x1+x2、x1x2、y1+y2，y1y2的值代入①式并整理得

又点P(x0,y0)为椭圆外一点，即

当x0y0=0时，所得符合题意的两切线的交点也满足方程

因此动点P的轨迹方程是x2+y2=13.

解法三　当两条切线斜率均存在且不为0时，设过点P的切线l的方程为y=k(x-x0)+y0，设椭圆上任一点为Q(3cosθ,2sinθ)，则点Q到l的距离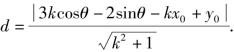

若l与椭圆相切，则即

又两切线垂直，则即

当一条切线的斜率不存在，另一条切线斜率为0时，易知P(±3，±2)满足x2+y2=13.

综上，点P的轨迹方程为x2+y2=13.

解法四　(运用柯西不等式)

当两条切线斜率均存在且不为0时，设过点P的直线l的方程是y=k(x-x0)+y0，椭圆上任一点为Q(x,y)，若直线与椭圆相切，则kx-y=kx0-y0存在最大(最小)值.

由柯西不等式知当且仅当时取等号.

则(kx0-y0)2=9k2+4时，直线l为切线.

整理得

又已知过点P向椭圆作的两条切线互相垂直，则

即得

而当其中一条切线的斜率不存在，另一条切线斜率为0时，易得P(±3，±2)满足

综上，点P的轨迹方程为x2+y2=13.

二、发散训练

1. 已知抛物线C：y2=2x的焦点为F，平行于x轴的两条直线l1,l2分别交C于A,B两点，交C的准线于P,Q两点.

(1)若F在线段AB上，R是PQ的中点，证明：AR∥FQ；

(2)若△PQF的面积是△ABF的面积的两倍，求AB中点的轨迹方程.

2. 已知圆x2+y2=1，点A(1，0),△ABC内接于该圆，且∠BAC=60°，当B，C在圆上运动时，求BC中点的轨迹方程.