构造法在解析几何中的应用-李正兴高中数学微专题中的压轴题攻略

构造法在解析几何问题中的应用主要体现在以下两个方面.

(1)解析几何模型是一种代数化的形式，即用代数的方法解答解析几何中的问题，在解题过程中势必要运用代数的构造方法，从而将解题过程进行到底.比如在研究直线与圆锥曲线位置关系时经常面对相交弦问题、最值问题、定值问题、定点问题、定直线问题，就需要使用方程的根的构造法、方程组解的构造法、函数模型构造法、重要恒等式、不等式的构造性方法，从而使解析几何问题获得简捷的代数解法.

(2)把各种类型的代数题或实际问题，通过分析、观察和试验，合理地将所研究的问题转化为几何模型，特别是通过构造解析几何模型、运用两点间距离公式、点到直线的距离公式、斜率公式、直线方程以及圆锥曲线方程可以巧妙地解决许多数学问题.而构造的过程是发散思维和创造性思维的过程.通过联想而构造相应的解析几何模型是数学核心素养的体现.

一、例题精讲

例1　(1)解方程

(2)解方程

(3)求函数的最大值.

解题策略　第(1)、第(2)问是解无理方程，如果直接移项、平方、再移项、再平方，则势必出现高次，而对于高次方程我们不一定能解，碰到特殊的高次方程，即使能解，运算也十分繁杂.而如果我们对方程左边实施配方，适当代换，把原方程转化为一个动点到两个定点的距离之和或距离之差，则原问题立即转变为解析几何问题.第(3)问，函数结构复杂，无法用常规方法解，若把两根式内部进行配方，转化为距离问题，则原问题向几何方向转化，一定会得到一种妙思巧解.

解：(1)原方程变形为

将方程中的常数“2”看作变量，即令2=y2，

则　①

令P(x,y),F1(-3,0),F2(3,0)，则①式为|PF1|+|PF2|=10.

由椭圆的定义可知，点P的轨迹为以F1、F2为焦点，长轴为10的椭圆，a=5,c=3，b2=a2-c2=16.其方程为

再将y2=2代入，求得原方程的解为

(2)原方程可以等价变形为

令1=y2，则有

令P(x，y)，F1(-5，0)，F2(5，0)，即|PF2|-|PF1|=6.点P的轨迹为以F1、F2为焦点，实轴长为6的双曲线左支，a=3，c=5，b2=c2-a2=16.

其方程为

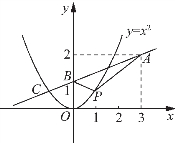
图3-35

再将y2=1代入，求得原方程的解为

(3)将给定的函数表达式变形为问题转化为求点P(x，x2)到点A(3，2)与B(0，1)距离之差的最大值.而P点的轨迹为抛物线，如图3-35所示.

由A、B的位置知直线AB必交抛物线y=x2于第二象限的一点C，由三角形两边之差小于第三边可知P位于C时，f(x)才能取到最大值.

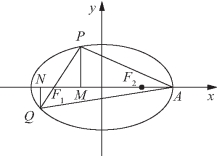
图3-36

例2　如图3-36所示，过椭圆的左焦点F1作一直线交椭圆于P、Q两点，A为椭圆的右顶点，求△PAQ面积的最大值.

解题策略　引进PQ的斜率k为参数，求△PAQ面积S关于k的解析式，通常求弦长|PQ|及点A到直线PQ的距离，或以|AF1|为底，设P(x1，y1),Q(x2，y2)，则|y1-y2|为高，很容易获得解析式(PQ斜率不存在的情况必须另行讨论)，显然，不管如何求，所得的解析式一定是无理式，而对无理函数的最值问题的求解是一个难点，关键是看解题者对SPAQ=f(k)如何变形构造，不同的构造可以朝不同的知识转化，得到不同的解法，构造能力越强，破解方法也越多.

解：∵F1(-1，0)，A(2，0)，且当直线PQ的斜率不存在时，

当直线PQ的斜率存在时，设直线PQ的方程为

y=k(x+1)(k≠0)，P(x1,y1)，Q(x2,y2)，

联立方程组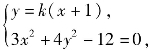　消去x并整理得(3+4k2)y2-6ky-9k2=0，显然Δ=36k2+36k2(3+4k2)>0.

∴|y1-y2|(www.xing528.com)

或联立方程组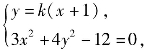消去y并整理得(3+4k2)x2+8k2x+4k2-12=0,

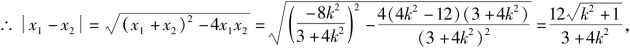
又∵A(2,0)到直线y=k(x+1)的距离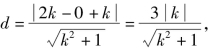

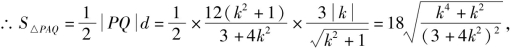
记S△PAQ=S，则

可见上述两种解法中得到的解析式是一样的，解题的关键在于如何求函数的最大值.思考角度之一是通过配方、换元转化为二次函数；思考角度之二是去分母后转化为二次方程(双二次)运用判别式法；思考角度之三是通过换元转化为三角函数，再次换元转化为“耐克函数”求最值，思考角度之四是通过分离常数后结合放缩法求g(k)的取值范围，进而求S的取值范围.

解法一　g(k)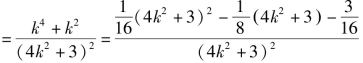

令则

又∵φ(t)在上是减函数，

即 也即从而

而当PQ⊥x轴时故△PAQ面积的最大值为

解法二　设k=tanθ，其中则

g(k)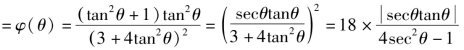

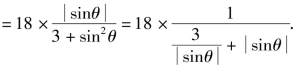
设则函数h(t)在(0,1)上是减函数，∴h(t)>h(1)=4,

当时，

综上，△PAQ面积的最大值为

解法三　g(k)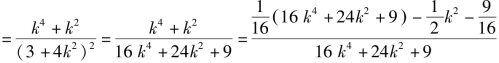

当时，

综上，△PAQ面积的最大值为

解法四　g(k)

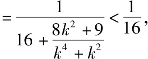
以下同解法三.

二、发散训练

1. 已知a、b满足b2=8a，求证：

2. 已知求|3x-4y-100|的最值.