平面向量及其运算特点是融数、形于一体，因为它具有代数形式和几何形式的双重身份，是中学数学知识的一个重要交汇点.平面向量的运算法则，特别是坐标运算可将几何问题转化为代数问题而解析几何的学科特点正是运用代数的方法研究平面图形的性质，两者是何等的一致！所以两者的结合或者说运用平面向量来解决解析几何问题是一件十分自然的事情，可谓是“竹外桃花三两枝，春江水暖鸭先知”了！平面向量与解析几何的交叉渗透，水乳交融，使数学问题的情境新颖别致，使解答过程如行云流水、自然流畅、赏心悦目，使数学之美充分展现，丰富多彩.
一、例题精讲
例1 (1)已知F为抛物线y2=x的焦点，点A,B在该抛物线上且位于x轴的两侧，
(其中O为坐标原点)，则△ABO与△AFO面积之和的最小值是( ).
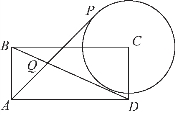
图3-31
A.2 B.3
(2)如图3-31所示，在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上，若
则λ+μ的最大值为( ).
解题策略 本例两小题是平面向量与解析几何的交汇，在考查直线与抛物线、直线与圆位置关系及最值求法的同时，还考查平面向量的坐标运算、数量积等的应用、不等式知识与三角知识的应用.
解：(1)设点A(x1，y1)，B(x2，y2)(不妨假设y1>0，y2<0)，
直线AB的方程为x=ty+m,与x轴的交点为M(m，0).
由
消去x得y2-ty-m=0，∴y1y2=-m.
又
解得y1y2=-2或1.
∵点A、B在抛物线上且位于x轴的两侧，∴y1y2=-2，故m=2.又
于是S△ABO+S△AFO
当且仅当
即
时取等号.
∴△ABO与△AFO面积之和的最小值是3，故选B.
图3-32
(2)解法一 如图3-32所示，建立平面直角坐标系，计算得
设P(m,n),
由
得(m,n)=λ(0，1)+μ(2，0)，
∴m=2μ，n=λ.动点P(m,n)在圆C上，
由三角换元得
故选A.
解法二 设动点P(x,y),点P的轨迹方程为
由
得
即直线x+2y-2z=0与圆相交，
故圆心到直线的距离小于等于半径，即
∴1≤z≤3，故λ+μ≤3，故选A.
解法三 由解法二将
代入
整理得
25x2-20(z+3)x+20z2-40z+84=0方程有解，由Δ≥0得z2-4z+3≤0，
∴1≤z≤3，故λ+μ≤3，故选A.
例2 已知一条曲线C在y轴右边，C上每一点到点F(1，0)的距离减去它到y轴距离的差都是1.
(1)求曲线C的方程，
(2)是否存在正数m，对于过点M(m，0)且与曲线C有两个交点A,B的任一直线，都有
？若存在，求出m的取值范围；若不存在，请说明理由.
解题策略 本例是解析几何与向量的综合，是高考命题的又一热点，求解时应注意根据向量式的特征，寻求其几何意义或将向量式转化为坐标式，根据其几何意义或坐标特征，寻求解题思路，当题中涉及两直线所成角时可转化为向量，而本例给出的
是否存在的探讨，则可利用数量积求解.
解：(1)设P(x,y)是曲线C上任意一点，那么点P(x,y)满足
化简得y2=4x(x>0).
(2)设过点M(m，0)(m>0)的直线l与曲线C的交点为A(x1，y1)，B(x2，y2).
设l的方程为x=ty+m,由
得y2-4ty-4m=0，
Δ=16(t2+m)>0，于是
①
又
②
又
于是不等式②等价于
③
将①式代入不等式③，有m2-6m+1<4t2. ④
对任意实数t，4t2的最小值为0，
∴不等式④对于一切t成立等价于m2-6m+1<0，即
由此可知，存在正数m，对于过点M(m，0)且与曲线C有两个交点A,B的任一直线，都有
且m的取值范围是
例3 在平面直角坐标系xOy中,O为坐标原点，动点P与两个定点M(1，0)、N(4，0)的距离之比为
(1)求动点P的轨迹W的方程；
(2)若直线l：y=kx+3与曲线W交于A，B两点，在曲线W上是否存在一点Q，使得
？若存在，求出此时直线l的斜率；若不存在，说明理由.
解题策略 第(1)问，由直接法求出动点P的轨迹W的方程，不难得出是一个圆，由于圆具有完美的对称性，在第(2)问中，若存在点Q使
根据向量的加法以及
易得四边形OAQB为菱形.对于解析几何问题的解决，其思维特征是：以几何特征寻找代数关系，以代数关系挖掘几何特征.
解：(1)设点P的坐标为(x,y)，依题意有
即
化简得x2+y2=4.
∴动点P的轨迹W的方程为x2+y2=4.
(2)解法一 ∵直线l：y=kx+3与曲线W：x2+y2=4相交于A，B两点，原点到直线l的距离
或
假设存在点Q,使得
(www.xing528.com)
∵A，B在圆上，且
由向量加法的平行四边形法则可知四边形OAQB为菱形，∴OQ与AB互相垂直平分，进而得到原点O到直线l：y=kx+3的距离为d=
|OQ|=1,即
解得
经验证k的值满足条件.
∴存在点Q，使得
解法二 ∵直线l：y=kx+3与曲线W：x2+y2=4相交于A，B两点，联立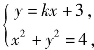
消去y得(k2+1)x2+6kx+5=0.
由Δ=36k2-20(k2+1)>0，得
或
设A(x1，y1)，B(x2，y2)，则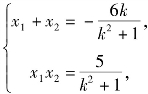
假设存在点Q(x,y)，使得
则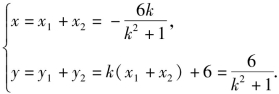
∵点Q(x,y)在圆x2+y2=4上，
解得
经验证k的值满足条件，∴存在点Q，使得
例4 已知曲线C上的动点M到y轴的距离比到点F(1，0)的距离小1.
(1)求曲线C的方程；
(2)过F作弦PQ、RS，设PQ、RS的中点分别为A，B.若
求
取最小值时，弦PQ、RS所在直线的方程；
(3)是否存在一定点T,使得
？若存在，求出T的坐标；若不存在，试说明理由.
解题策略 第(1)问，易得动点M到直线x=-1的距离与到点F(1，0)的距离相等，符合抛物线的定义，由求轨迹方程的定义法，即得曲线C的方程；第(2)问，以直线PQ的斜率k为参数，则易得RS的斜率为
分别求出A，B坐标(在求出A点坐标后，把坐标中的k用
代，即得B点的坐标)，从而求得向量
的模，并运用均值不等式求
的最小值，由等号成立的条件确定k的值，得PQ、RS所在直线的方程；第(3)问，是探索性问题，首先由条件
通过向量变形可确定A，T，B三点共线，再探求直线AB是否过定点.本例看似难度不高，但步步紧扣、层层深入，解析几何常用的方程理论与平面向量的运算融为一体，正所谓“青山缭绕疑无路，忽见千帆隐映来”，解题者在解题过程中碰到阻隔在所难免，想办法穿越阻隔，前面就是坦途，风景无限好！
解：(1)由条件M到F(1，0)的距离等于到直线x=-1的距离，曲线C是以F为焦点，直线x=-1为准线的抛物线，其方程为y2=4x.
(2)设lPQ：y=k(x-1)，代入y2=4x得：k2x2-2(k2+2)x+k2=0.由韦达定理得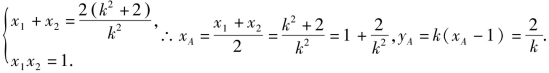
∴PQ⊥RS，只要将A点坐标中的k换成
得B(1+2k2，-2k).
故
当且仅当k=±1时取
最小时，弦PQ、RS所在的直线方程为y=±(x-1)，
即x+y-1=0或x-y-1=0.
(3)
即A，T，B三点共线.
∴是否存在一定点T，使得
即探求直线AB是否过定点.
由(2)知，直线AB的方程为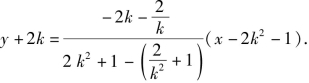
即(1-k2)y=k(x-3).∴直线AB过定点(3，0).
故存在一定点T(3，0)，使得
例5 设椭圆
过点
且左焦点为
(1)求椭圆C的方程；
(2)当过点P(4，1)的动直线l与椭圆C相交于两不同点A，B时，在线段AB上取点Q，满足
证明：点Q总在某定直线上.
解题策略 本例是具有射影几何背景的解析几何试题，考查直线、椭圆的方程及其几何性质、线段定比分点公式的应用.第(2)小题的求解是一个难点，下面提供的两种解法都是抓住A，P，B，Q四点共线来展开的，这是解决本小题的突破口.
解：(1)由题意，得
解得a2=4，b2=2.
所求椭圆方程为
(2)证法一 设Q、A、B的坐标分别为(x,y)，(x1，y1)，(x2，y2),由题设知
均不为零，记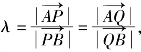
则λ>0，且λ≠1.又A，P，B，Q四点共线，从而
于是有
从而
①
②
又点A，B在椭圆C上，
即
③
④
①+②×2并结合③④得4x+2y=4.
即点Q(x,y)总在定直线2x+y-2=0上.
证法二 设点Q(x,y)，A(x1，y1)，B(x2，y2).
由题设知
均不为零，且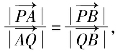
又P、A、Q、B四点共线，可设
于是
①
②
由于A(x1，y1)，B(x2，y2)在椭圆C上，将①②分别代入C的方程x2+2y2=4.整理得(x2+2y2-4)λ2-4(2x+y-2)λ+14=0， ③
(x2+2y2-4)λ2+4(2x+y-2)λ+14=0， ④
④-③得8(2x+y-2)λ=0，∵λ≠0，∴2x+y-2=0.
即点Q(x,y)总在定直线2x+y-2=0上.
二、发散训练
1. 如图3-33所示，设抛物线C：y=x2的焦点为F，动点P在直线l：x-y-2=0上运动，过P作抛物线C的两条切线PA,PB,切点分别为A,B.求证：∠AFP=∠BFP.
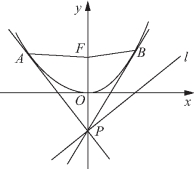
图3-33
2. 如图3-34所示，在△ABC中，已知A(-3,0)，B(3，0).CD⊥AB于D，若H为△ABC的垂心,且
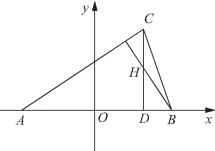
图3-34
(1)求点H的轨迹方程；
(2)设P(-1，0)、Q(1，0)，是否存在这样的H点，使得
成等差数列？如果存在，求出H点坐标，如果不存在，请说明理由；
(3)设直线AH，BH 与直线l：x=9分别交于M、N点，请问：以MN为直径的圆是否经过点H的轨迹外的定点？并说明理由.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
