解析几何问题通常是用代数的方法来求解的，在求解过程中使几何问题向代数问题转化，常常需要用平面几何的知识和方法来辅助分析并巧妙地解决，常用的平面几何知识主要如下.
(1)直角三角形中有关性质：斜边长大于直角边长、勾股定理、射影定理.
(2)一般斜三角形中有关性质：三角形两边之和大于第三边,两边之差小于第三边.正弦定理、余弦定理、三角形面积公式、三角形的“五心”(重心、垂心、内心、外心、旁心)及其有关结论、三角形中位线定理、两个三角形的相似或全等.
(3)圆的有关性质：垂径定理、切割线定理、相交弦定理.
一、例题精讲
例1 (1)已知线段AB的长为a，点P在线段AB上运动，在AB的同侧分别作正三角形APM和正三角形PBN，求线段MN的中点Q的轨迹方程；
(2)设圆x2+y2-4x-5=0的弦AB的中点为Q(3，1)，直线AB交x轴于点P，求|PA||PB|.
(3)已知圆C：x2+y2-2x+4y-4=0，是否存在斜率为1的直线l，使l被C截得的弦AB为直径的圆过原点？若存在，求出l的方程；若不存在，说明理由.
解题策略 第(1)问，过M、N两点作x轴的垂线，构造梯形，根据Q为MN的中点，构造梯形中位线，通过平面几何梯形中位线性质，确定Q点满足的几何条件，得出点Q的轨迹方程，这种求轨迹方程的方法称为几何法，即利用平面几何知识得到包含已知量和动点坐标的关系式，化简后得到动点的轨迹方程.第(2)问，由条件知点P在圆外，过点P的直线与圆C相交于A，B两点，x轴过点P与圆C相交于M、N两点，满足了运用相交弦定理的场景，运用圆的相交弦定理很容易求得结果.第(3)问“以AB为直径的圆过原点”，即
也即AO⊥BO，可转化为以下3种方法解题：方法一，利用平面几何知识，直角三角形三边长满足勾股定理、直角三角形斜边上的中线等于斜边的一半；方法二，选择方程组法及圆上任一点与直径的两端点的连线互相垂直，利用向量数量积为0来解；方法三，由上所述半圆上的圆周角是直角，得出kOAkOB=-1,在后两种解法中，若设A(x1，y1),B(x2，y2),则必有x1x2+y1y2=0.韦达定理、方程理论在解题中是一定用到的.
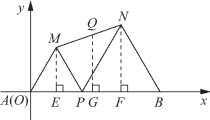
图3-24
解：(1)建立如图3-24所示的平面直角坐标系，并设点Q的坐标为(x，y)，分别过M、N、Q作x轴的垂线，垂足分别为E、F、G，则GQ是梯形MNFE的中位线，由梯形中位线定理知
即
又
线段MN的中点Q的轨迹方程为
(2)由已知得圆心C(2,0)，∵Q(3,1)为弦AB的中点，∴CQ⊥AB.
又∵kCQ=-1,∴kAB=1，可得直线AB的方程为x+y-4=0.
∴直线AB交x轴于点P(4,0).
又∵圆C与x轴的交点为M(-1,0)，N(5,0)，∴|PM|=5,|PN|=1,由圆的相交弦定理得|PA|·|PB|=|PM|·|PN|=5.
(3)解法一 圆C化为标准方程是：(x-1)2+(y+2)2=32.
假设存在以AB为直径的圆M，圆心M的坐标为(a,b).
由于
即a+b+1=0,
得b=-a-1, ①
直线l的方程为y-b=x-a，即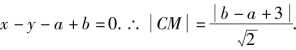
∴以AB为直径的圆M过原点,∴|MA|=|MB|=|OM|.
②
把①式代入②式得
或a=-1.
当
时，
此时直线l的方程为：x-y-4=0；
当a=-1时，b=0，此时直线l的方程为：x-y+1=0.
故这样的直线l是存在的，方程为x-y-4=0或x-y+1=0.
解法二 设存在斜率为1的直线l，使l被圆C截得的弦AB为直径的圆过原点且l:y=x+m.
由
得2x2+2(m+1)x+m2+4m-4=0.
Δ=4(m+1)2-8(m2+4m-4)=-4(m2+6m-9).
设A(x1,y1),B(x2,y2)，则
∵弦AB为直径的圆过原点，∴x1x2+y1y2=0，
即2x1x2+m(x1+x2)+m2=0,
∴m2+4m-4+m(-m-1)+m2=0,即m2+3m-4=0,解得m=-4或m=1.
经检验，Δ>0.
故这样的直线l是存在的，方程为x-y-4=0或x-y+1=0.
例2 (1)AB为过抛物线y2=4x焦点F的弦，O为坐标原点，且∠OFA=135°，C为抛物线准线与x轴的交点，则∠ACB的正切值为( ).
(2)过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点，O为坐标原点，若|AF|=3,则△AOB的面积为( ).
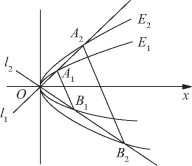
图3-25(www.xing528.com)
(3)过圆锥曲线E的一个焦点F的直线(不与焦点所在的对称轴重合)交E于不同两点A，B，这两点和E上任一点C的连线AC，BC分别和F的对应准线l交于M，N，证明：以MN为直径的圆必过焦点F.
(4)如图3-25所示，已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0)，过原点O的两条直线l1和l2，l1与E1、E2分别交于A1、A2，l2与E1、E2分别交于B1、B2两点.过原点O作直线L(异于l1,l2)与E1、E2分别交于C1、C2两点，记△A1B1C1与△A2B2C2的面积分别为S1与S2，求
的值.
解题策略 第(1)问，可以通过求斜率kCA,kCB,再用夹角公式求tan∠ACB，但若构造符合题意的直角梯形，利用平面几何结合三角函数定义解则更具“奇思妙想”；第(2)问，形式简洁，入口较宽，可以有多种解法，这里介绍平面几何的方法，一是利用三角形相似解，二是由三角形面积用排除法解，别具一格；第(3)问，由三角形外角平分线性质定理的逆定理证明相当简洁；第(4)问，利用相似三角形面积比等于边长的平方比解能迅速找到突破口.
解：(1)解法一 焦点F(1，0)，C(-1，0)，AB方程为y=x-1，与抛物线方程y2=4x联立，解得
于是
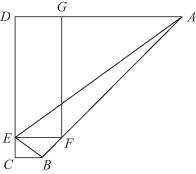
图3-26
解法二 如图3-26所示，利用抛物线的定义，将原题转化为：在直角梯形ABCD中，∠BAD=45°，EF∥DA，EF=2，AF=AD，BF=BC,求∠AEB.
类似的,有
图3-27
∠AEB=∠AEF+∠BEF=2∠AEF.
故选A.
(2)解法一 (平面几何法)过A,B两点分别作准线l的垂线，垂足分别为P,Q，过B作BE⊥AP,垂足为E点，且交x轴于H点，(如图3-27所示)令|BQ|=|BF|=x.则|HF|=2-x,|AE|=3-x,由三角形相似得
即
解得
故
设∠AFx=θ，则由抛物线的焦点弦长公式得
解得
故选C.
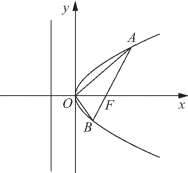
图3-28
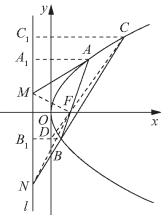
图3-29
解法二 (排除法)不妨设点A在x轴的上方，由A点坐标为
可知
可排除A、B选项.
又明显有S△BOF<S△AOF，如图3-28所示，
可排除D选项，故选C.
(3)证明 如图3-29所示，联结MF,NF,并作AA1⊥l，BB1⊥l，CC1⊥l,A1,B1,C1为垂足，D为CF延长线上一点.
(E的离心率).
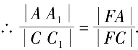
又∵AA1∥CC1.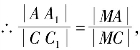
故
由三角形外角平分线性质定理的逆定理，得MF平分∠AFD,同理，NF平分∠BFD,且∠AFD+∠BFD=180°.因此，∠MFN=90°,即以MN为直径的圆过焦点F.
(4)设直线l1、l2的方程分别为y=k1x，y=k2x(k1、k2≠0)，则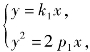
得
由
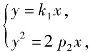得
同理可得
∴
故
同理可得B1C1∥B2C2,C1A1∥C2A2.
∴△A1B1C1∽△A2B2C2，因此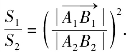
又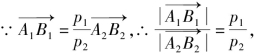
故
二、发散训练
1. 已知椭圆
的左右焦点分别为F1与F2，点P在直线
上，当∠F1PF2取最大值时，求
的值.
2. 如图3-30所示，过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M,N两点，自M,N向准线l作垂线，垂足分别为M1,N1.
(1)求证：FM1⊥FN1；
(2)记△FMM1，△FM1N1,△FNN1的面积分别为S1,S2,S3，试判断
是否成立？并证明你的结论.
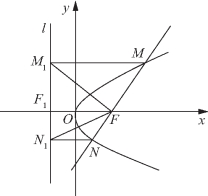
3-30
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
