从高考命题看,解析几何试题每年都在变换风格,考查思维的敏捷性,在改革中求发展,在探索中求创新,而直线与圆锥曲线综合问题是命题长盛不衰的热点,解析几何中的信息迁移题和应用性问题也会有所加强.
综合问题通常是一些基本问题的组合,所以在解综合题时,可通过审题确定解题的策略,把问题分解成若干个基本问题,因此掌握基本问题的求解方法是解综合题的先决条件.我们用代数的方法研究几何图形的性态,从解析几何角度看常见题型不外乎是轨迹问题(见本书第四十九讲)、对称问题(见本书第四十二讲)、最值问题与范围问题(见本书第四十四讲)、定点、定值问题(见本书第四十三讲)、弦中点问题、交点问题、弦长问题(直线与圆锥曲线的相交弦问题).本讲对上述的后3个问题略作展开.
一、例题精讲
例1 (2018年高考数学全国卷Ⅲ理科第20题)
已知斜率为k的直线l与椭圆![]() 交于A,B两点,线段AB的中点为M(1,m)(m>0).
交于A,B两点,线段AB的中点为M(1,m)(m>0).
(1)证明:![]()
(2)设F为C的右焦点,P为C上一点,且![]() 证明:
证明:![]() 等差数列,并求该数列的公差.
等差数列,并求该数列的公差.
解题策略 本题主要考查直线与椭圆的位置关系、不等式的性质以及等差数列的证明,涉及平面向量的知识,考查函数与方程、数形结合、转化与化归等数学思想方法,考查的核心素养是数学抽象、逻辑推理、数学运算.直线与椭圆的位置关系主要是通过韦达定理表示出相应的“几何量”、“几何关系”,因此要掌握常见的求“几何量”(如长度等)、“几何关系”(如平行、垂直等)的方法.第(1)问,可以利用直线的斜率、直线与椭圆的位置关系及中点,得到一个关于m、k的关系式,然后根据m的取值范围求解.具体操作上有多种方法,如点差法、判别式法、通过作原椭圆关于点M(1,m)的对称椭圆、利用直线的参数方程等.第(2)问,利用已知条件中的向量关系证明![]() 成等差数列,即证明
成等差数列,即证明![]() 若设A(x1,y1),B(x2,y2),P(x0,y0),则由条件
若设A(x1,y1),B(x2,y2),P(x0,y0),则由条件![]() 结合中点坐标公式可得x1+x2=2,y1+y2=2m,进而求m的值,如果利用椭圆第二定义求焦半径|FA|,|FB|可以避免复杂的计算,倘若从几何意义上挖掘,可知F点为A、B、P构成△ABP的重心,显然是妙思巧解.
结合中点坐标公式可得x1+x2=2,y1+y2=2m,进而求m的值,如果利用椭圆第二定义求焦半径|FA|,|FB|可以避免复杂的计算,倘若从几何意义上挖掘,可知F点为A、B、P构成△ABP的重心,显然是妙思巧解.
解:(1)证法一 (设而不求、点差法) 设A(x1,y1),B(x2,y2).
则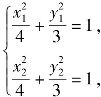 两式相减,并由
两式相减,并由![]() 得
得![]()
由题设知![]() 于是
于是![]()
由题设得![]() 故
故![]()
证法二 (判别式法) 设l的方程为y=kx+n,与椭圆C联立,
消去y得(4k2+3)x2+8knx+4n2-12=0.
设A(x1,y1),B(x2,y2).则由Δ>0,∴4k2+3>n2, ①
![]() ②
②
则![]() 且k<0.
且k<0.
由①②得![]()
证法三 (利用对称思想方法)
对原椭圆作关于M(1,m)的对称的椭圆为![]()
两椭圆方程相减可得![]() 即为AB所在直线方程,也即为两椭圆公共弦所在直线方程.故
即为AB所在直线方程,也即为两椭圆公共弦所在直线方程.故![]()
又点M(1,m)在椭圆C内部可得![]() 可得
可得![]()
![]()
证法四 (利用直线的参数方程)
设直线l的参数方程为![]() (θ为l的倾斜角,t为参数),代入椭圆C的方程得(3cos2θ+4sin2θ)t2+(6cosθ+8msinθ)t-9+4m2=0.设t1t2是线段两端点A,B对应的参数,M(1,m)是线段AB中点,知t1+t2=0得
(θ为l的倾斜角,t为参数),代入椭圆C的方程得(3cos2θ+4sin2θ)t2+(6cosθ+8msinθ)t-9+4m2=0.设t1t2是线段两端点A,B对应的参数,M(1,m)是线段AB中点,知t1+t2=0得![]()
点M(1,m)在椭圆C内,![]() 可得
可得![]()
(2)证法一 (根据题设![]() 求出点P坐标,解出m,得到直线l的方程,联立直线l与椭圆C的方程,由根与系数关系进行证明)
求出点P坐标,解出m,得到直线l的方程,联立直线l与椭圆C的方程,由根与系数关系进行证明)
由题意得F(1,0),设P(x0,y0),由题设![]()
得(x0-1,y0)+(x1-1,y1)+(x2-1,y2)=(0,0).
结合(1)的结果得x0=3-(x1+x2)=1,y0=-(y1+y2)=-2m<0,
又点P在C上,![]() 从而
从而![]() 于是
于是![]() 同理
同理![]()
![]()
故![]() 即
即![]() 成等差数列.
成等差数列.
设该数列的公差为d.
则![]() , ①
, ①
将![]() 代入
代入![]() 得k=-1.
得k=-1.
∴l的方程为![]() 代入C的方程,并整理得
代入C的方程,并整理得![]()
故![]() 代入①解得
代入①解得![]()
∴该数列的公差为![]() 或
或![]()
证法二 (利用椭圆焦半径公式)
![]()
又∵点P在椭圆上且![]()
∴![]() 由(1)的解答可知
由(1)的解答可知![]() 直线l的方程为:
直线l的方程为:![]()
直线l的方程与椭圆方程联立,得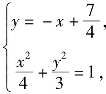
消去y化简得28x2-56x+1=0,则![]()
由焦半径公式得![]() 而
而![]()
可得![]()
又![]()
![]() 成等差数列.
成等差数列.
设公差为d,则有![]()
![]() 或
或![]()
证法三 (利用三角形重心)
设A(x1,y1),B(x2,y2),P(x0,y0).
显然点F为△ABP的重心,易得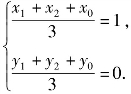
注意到M为AB的中点,易得![]() 进而可得k=-1,再由重心性质得
进而可得k=-1,再由重心性质得![]() 可得AB所在直线方程为
可得AB所在直线方程为![]()
以下同证法一、证法二.
例2 (2018年高考数学江苏卷第18题)
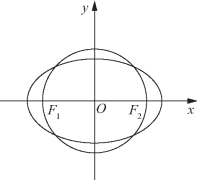
图3-22(https://www.xing528.com)
如图3-22所示,在平面直角坐标系xOy中,椭圆C过点![]() 焦点
焦点![]() 圆O的直径为F1F2.
圆O的直径为F1F2.
(1)求椭圆C及圆O的方程;
(2)设直线l与圆O相切于第一象限内的点P.
(i)若直线l与椭圆C有且只有一个公共点,求点P的坐标;
(ii)直线l与椭圆C交于A,B两点,若△OAB的面积为![]() 求直线l的方程.
求直线l的方程.
解题策略 本题主要考查直线方程、圆的方程、圆的几何性质、椭圆方程、椭圆的几何性质、直线与圆及椭圆的位置关系,考查分析问题能力和运算求解能力.第(1)问,利用椭圆的几何性质求圆的方程和椭圆的方程.第(2)问,(i)利用直线与圆、椭圆的位置关系建立方程求解;(ii)结合(i),利用弦长公式、三角形的面积公式求解.第(2)问在求解时可设P点的坐标为(x0,y0)(x0>0,y0>0).也可设三角式,即![]() 从而得到各具特色的解法.
从而得到各具特色的解法.
解:(1)∵椭圆C的焦点为![]() 可设椭圆C的方程为
可设椭圆C的方程为![]() 又点
又点![]() 在椭圆C上.
在椭圆C上.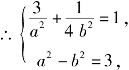 解得
解得![]()
因此,椭圆C的方程为![]() 圆O的直径为F1F2,∴其方程为x2+y2=3.
圆O的直径为F1F2,∴其方程为x2+y2=3.
(2)解法一 (i)设直线l与圆O相切于P(x0,y0)(x0>0,y0>0).则![]() 的方程为
的方程为![]() 即
即![]()
由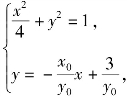 消去y得
消去y得![]() ①
①
∵直线l与椭圆C有且只有一个公共点,
![]()
![]()
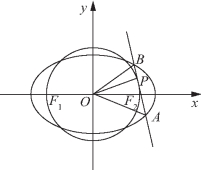
图3-23
因此,点P的坐标为![]()
(ii)如图3-23所示.∵三角形OAB的面积为![]() 从而
从而![]()
设A(x1,y1),B(x2,y2),
由①得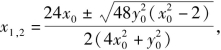
![]()
![]() 即
即![]()
解得![]() 舍去),则
舍去),则![]() 因此P的坐标为
因此P的坐标为![]()
综上,直线l的方程为![]()
解法二 设P点坐标为![]()
∵原点到直线![]() 的距离
的距离![]()
∴与圆O切于点P的直线l的方程为![]()
由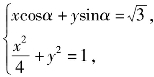 消去y得
消去y得![]()
(i)∵直线l与椭圆相切,∴Δ=-16(cos2α-2)(3cos2α-2)=0,
![]() 故
故![]()
∴P点坐标为![]()
(ii)∵直线![]() 与圆O相切,
与圆O相切,
∴△OAB中边AB上的高为![]()
∵△OAB的面积为![]()
设A(x1,y1),B(x2,y2),由(i)知
![]()
|AB|![]()
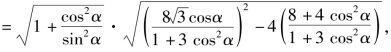
即18cos6α-153cos4α+235cos2α-100=0,
即(6cos2α-5)(cos2α-1)(3cos2α-20)=0.
![]() 故
故![]()
∴直线l的方程为![]()
解法三 设P点坐标为![]()
则与圆O切于点P的直线l的参数方程为:
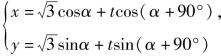 (t为参数),即
(t为参数),即 (t为参数).
(t为参数).
代入![]() 得关于t的一元二次方程
得关于t的一元二次方程
![]()
(i)∵直线l与椭圆相切,![]()
![]() 故
故![]()
∴P点坐标为![]()
(ii)同解法二,此处略.
二、发散训练
1. 在平面直角坐标系xOy中,直线l:x=-2交x轴于点A,设P是l上一点,M是线段OP的垂直平分线上一点,且满足∠MPO=∠AOP.
(1)当点P在l上运动时,求点M的轨迹E的方程;
(2)已知T(1,-1),设H是E上动点,求|HO|+|HT|的最小值,并给出此时点H的坐标;
(3)过点T(1,-1)且不平行于y轴的直线l1与轨迹E有且只有两个不同的交点,求直线l1的斜率k的取值范围.
2. 设|y2-16x|=256-16|x|.
(1)记方程表示的曲线围成的封闭区域为D,试作出这个区域D;
(2)过抛物线y2=16x焦点的直线l与抛物线交于P、Q两点,若|PQ|=a,求S△OPQ;
(3)当过焦点的直线l与y2=16x在区域D内的部分相交于P、Q时,求S△OPQ的最大值.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




