高中数学微专题：解析几何的定点、定值问题

在解析几何中，有些几何量如直线的斜率、两点间的距离、图形的面积、线段或角的比值及基本几何量和变量无关，这类问题统称为定值问题.动直线或动曲线不论如何变化总是经过某定点，探求这个定点的坐标，就是解析几何中的定点问题.定点、定值问题的解法与证明题类似，在求定点、定值之前已经知道定点、定值的存在，尽管题中并未告知，要想办法把它求出来.一种思路是进行一般计算推理求出其结果，另一种是通过考察极端位置或用特殊值探路求之，再从一般情况下进行论证，也可以首先大胆设参，运算推理到最后参数必消，定点、定值显露.

探究动曲线(含直线)过定点问题以及证明与曲线上的动点有关的定值问题是高考解析几何命题中经常出现的题型.

一、例题精讲

例1　已知动点M到点F(1，0)的距离等于它到直线x=-1的距离.

(1)求点M的轨迹C的方程；

(2)过点F任意作互相垂直的两条直线l1，l2，分别交曲线C于点A、B和点M、N，设线段AB、MN的中点分别为P、Q，求证：直线PQ恒过一个定点.

解题策略　直线经过某个与参数无关的点，则直线或曲线的表示一定含有参变数，即直线系或曲线系，可将其方程变式为f(x，y)+λg(x，y)=0(其中λ为参变量)，由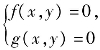确定定点坐标.当然，对于本题还可结合从特殊到一般的思想方法，可以先选择特征位置(如当k=±1时)，猜测出或找出要过的点，再就一般情形给予证明，通常也就是上述用待定系数法从“恒成立”的角度加以解决.

解：(1)设动点M(x，y)，由题意得化简得y2=4x.

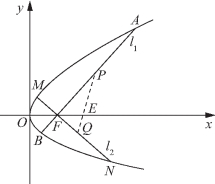
图3-15

∴点M的轨迹C的方程为y2=4x.

(本题可以由抛物线定义直接求得)

(2)证明　如图3-15所示，设点A(x1，y1)，B(x2，y2)，

则点由题意，可设直线l1的方程为y=k(x-1)(k≠0)，

由得k2x2-(2k2+4)x+k2=0.

Δ=(2k2+4)2-4k4=16k2+16>0.

∵直线l1与曲线C交于A，B两点，

∴有

∴点由题意知，直线l2的斜率为

同理可得点Q(1+2k2，-2k).

当k=±1时，有此时直线PQ的斜率为

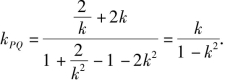
∴直线PQ的方程为即yk2+(x-3)k-y=0,

∴直线PQ恒过定点E(3，0).

当k=±1时，直线PQ的方程为x=3，也过点E(3，0).

综上，直线PQ恒过定点E(3，0).

例2　在平面直角坐标系xOy中，已知椭圆C的中心在坐标原点，对称轴为坐标轴，且过点

(1)求椭圆C的方程；

(2)设椭圆C上的任意一点R(x0，y0)，从原点O向圆R：(x-x0)2+(y-y0)2=8作两条切线，分别交椭圆于点P、Q，试探究OP2+OQ2是否为定值？若是，求出其值；若不是，请说明理由.

解题策略　解答本题的关键是对直线斜率是否存在的分类讨论，即由特殊到一般的思考方法.当斜率存在时，运用设而不求、整体变形的解题策略，应当指出的是在解析几何问题中，任何一个字母都具备成为参数与变量的双重属性，需要通过对方程形式的特征的观察、对比和研究来把握问题解决的方向.

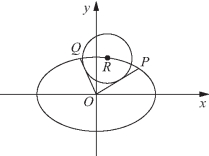
图3-16

解：(1)椭圆C的中心在原点，由题意，设此椭圆C的方程为mx2+ny2=1(m>0，n>0，m≠n).(www.xing528.com)

由椭圆过点

可得解之得

∴椭圆C的方程为

(2)直线OP、OQ与坐标轴重合时，易计算得OP2+OQ2=36.

当直线OP、OQ的斜率存在时，如图3-16所示，不妨设直线OP：y=k1x，OQ：y=k2x.

依题意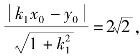化简得

同理有

∴k1、k2是方程的两个不相等的实数根.

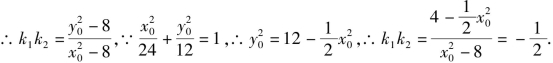
设P(x1，y1)、Q(x2，y2)，则

即

故

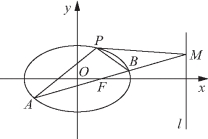
图3-17

例3　如图3-17所示，椭圆经过点离心率直线l的方程为x=4.

(1)求椭圆C的方程；

(2)AB是经过右焦点F的任一弦(不经过点P)，设直线AB与直线l相交于点M，记PA、PB、PM的斜率分别为k1、k2、k3，问：是否存在常数λ，使得k1+k2=λk3？若存在，求λ的值；若不存在，说明理由.

解题策略　对于探索某些几何量为定值的条件是否存在问题，通常先假设符合题意的几何条件存在，用这些条件表示为定值的几何量，化简整理，再求出参数或说明参数不存在.

解：(1)由在椭圆上，得　①

又由得a2=4c2，b2=3c2.　②

将②代入①得c2=1，a2=4，b2=3，故椭圆方程为

(2)设直线AB的方程为y=k(x-1)，A(x1，y1)，B(x2，y2).

由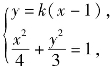得(4k2+3)x2-8k2x+4k2-12=0.

则k1+k2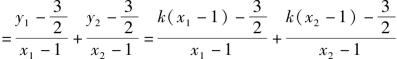

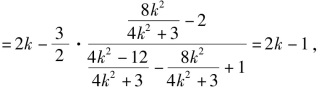
将x=4代入y=k(x-1),得M(4，3k)，则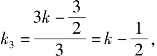则2k3=2k-1.

∴k1+k2=2k3，故存在常数λ=2符合题意.

二、发散训练

已知F是双曲线的一个焦点，过F作一条与坐标轴不垂直，且与渐近线也不平行的直线l，交双曲线于A，B两点，线段AB的中垂线l′交x轴于点M.

(1)设F为右焦点，l的斜率为1，求l′的方程；

(2)试判断是否为定值？说明理由.