解析几何是初等数学与高等数学的纽带，它本身侧重于数形结合、形象思维，而它的解题过程则是代数的，综合性很强，要求有较高的解题能力，因此历来是高考的重要内容、压轴题命制的热点.
解析几何综合问题多数以直线和圆锥曲线为背景，考查直线与圆锥曲线或圆锥曲线与圆锥曲线位置关系问题.近年来在压轴题中多次出现动直线与两条不同的圆锥曲线段所构成图形位置关系的讨论，涉及最值问题、参数范围问题、定点、定值问题等，形式以计算题、轨迹题为主，也有证明题以及探索研究性问题，从运用知识求解的过程看，一般以直线方程与圆锥曲线方程联立方程组转化为二次方程的理论为重点，从思维方法来分析，一是数形转化;二是方程观点；三是参数观点.
高考数学压轴题的本身或在其解答过程中涉及多个知识点或多个数学分支交汇的题型，并且解题思维方法具有多向性和灵活性，其目的重在测试思维能力和运用知识的能力，考查学生数学核心素养，由于压轴题的综合性强、涉及面广、题目结构较为复杂，很难给出固定的解题方法，只能根据具体问题分析题中已知与未知的关系，筑桥铺路，寻求解题的途径.
要解好压轴题就要读懂题，弄清条件是什么？条件与哪些知识有关？如何用好相关知识？可以作哪些转化？有些什么隐含的内容需要挖掘出来？从结论考虑，需要哪些条件才能得到结论？从已知到结论之间需要走多少路？有没有近路可走？各方面都考虑清楚了，解题思路也就逐步产生了！
一、例题精讲
例1 (2018年高考数学全国卷Ⅰ理科第19题)
设椭圆
的右焦点为F，过F的直线l与C交于A，B两点，点M的坐标为(2，0).
(1)当直线l与x轴垂直时，求直线AM的方程；
(2)设O为坐标原点，证明：∠OMA=∠OMB.
解题策略 本题考查椭圆的标准方程及其几何性质、直线与椭圆的位置关系，证明等角，考查学生的推理论证能力、运算求解能力，考查数形结合思想、化归与转化思想，考查的核心素养是逻辑推理、直观想象、数学运算.
本题来源于2015年全国Ⅰ卷理科数学第20题，把之前考题中的“抛物线”变为了“椭圆”，仍然考查直线与圆锥曲线有两个交点的位置关系，都是“求方程”与“证明等角”问题，只是去掉了原来的是否存在型的外包装.本讲把2015年的那道考题放在例2，读者可以把两题仔细对照比较，可以发现当今高考命题改革的方针仍然是“小步改、不停步”，通过改编、创新等手段来赋予高考典型试题新的生命，这也是高考命题的一种新走向，相似的例子是很多的，所以我们在复习备考的过程中可注意对近年来高考真题的训练，把握其实质，掌握其规律，规范其步骤，做到“胸中有高考真题”，以不变应万变.
从解题的战略战术上思考，破解此类解析几何题的关键：一是“图形”引路，一般需画出大致图形，把已知条件翻译到图形中，利用直线方程的点斜式或两点式，即可快速表示出直线方程；二是“转化”，即架起桥梁，把要证的两角相等，根据图形的特征，转化为斜率之间的关系，再把直线与椭圆的方程联立，利用根与系数的关系，以及斜率公式即可证得结论.
于是，第(1)问，先求出椭圆
的右焦点F的坐标，由于l与x轴垂直，所以可求出直线l的方程，从而求出点A的坐标，再利用直线方程的两点式，即可求出直线AM的方程.第(2)问，常规证法是对直线l分3类讨论：(i)当直线l与x轴重合时，直接求出∠OMA=∠OMB=0°.(ii)当直线l与x轴垂直时，可直接证得∠OMA=∠OMB.(iii)当直线l与x轴不重合也不垂直时，设l的方程为y=k(x-1)(k≠0)，A(x1，y1)，B(x2，y2)，利用斜率公式表示出kMA+kMB，把直线l的方程代入椭圆C的方程，消去y转化为关于x的一元二次方程，利用根与系数的关系即可证明kMA+kMB=0，从而证明∠OMA=∠OMB.当然，若设l的方程为x=my+1可减少分类讨论的步骤，若能再进一步抓住椭圆对称的性质，还可简化解题过程，若在解题过程中结合平面几何知识，即运用角平分线定理的逆定理，把角相等的证明转化为距离相等的证明，别具一格.还有诸如利用直线的参数方程、运用椭圆的第二定义，转化为极坐标后证明，解题过程都比较简捷,都可以说是妙思巧解.
解：(1)由已知得F(1，0)，l的方程为x=1.
由已知可得，点A的坐标为
或
∴AM的方程为
或
(2)证法一 (证明∠OMA=∠OMB转化为证kMA+kMB=0)
当l与x轴重合时，∠OMA=∠OMB=0°.
当l与x轴垂直时，OM为AB的垂直平分线，∴∠OMA=∠OMB.
当l与x轴不重合也不垂直时，设l的方程为y=k(x-1)(k≠0)，A(x1，y1)，B(x2，y2)，则
直线MA，MB的斜率之和为
由y1=kx1-k，y2=kx2-k得
将y=k(x-1)代入
得(2k2+1)x2-4k2x+2k2-2=0.
则
从而kMA+kMB=0，故MA，MB的倾斜角互补，∴∠OMA=∠OMB.
综上，∠OMA=∠OMB.
证法二 (设l的方程为x=my+1，避免对l斜率不存在的讨论)
当直线l与x轴重合或垂直时，显然有∠OMA=∠OMB.
当直线l与x轴不垂直也不重合时，设直线l的方程为x=my+1，交椭圆于A(x1，y1)，B(x2，y2).
由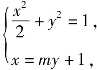
得(m2+2)y2+2my-1=0.
由韦达定理得
点A关于x轴的对称点N(x1，-y1)，则直线BN的方程为
(y+y1)(x2-x1)=(y1+y2)(x-x1).
令y=0，x
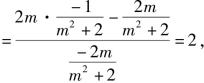则直线BN过点M，∠OMA=∠OMB.
证法三 (结合平面几何角平分线定理的逆定理，证∠OMA=∠OMB转化为证角平分线上任意一点到角两边距离相等)
设点O(也可选点F)到直线MA，MB的距离分别为d1，d2，根据角平分线定理的逆定理，要证∠OMA=∠OMB，只需证d1=d2.
当直线l的斜率为0时，易得d1=d2=0.
当直线l的斜率不为0时，设直线l的方程为：x=my+1，A(x1，y1)，B(x2，y2).
由方程组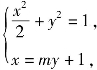
得(m2+2)y2+2my-1=0，Δ>0恒成立，
直线MA的方程为：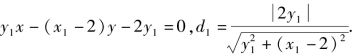
∵点A在直线l上，∴x1=my1+1，故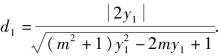
同理，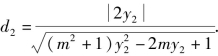
即d1=d2.
综上，∠OMA=∠OMB.
证法四 (利用直线l的参数方程)
设直线l的参数方程为
(t为参数). ①
将①式代入椭圆方程
中，整理得(1+sin2α)t2+2cosαt-1=0.
则
又A(1+t1cosα，t1sinα)，B(1+t2cosα，t2sinα)，
则kMA+kMB
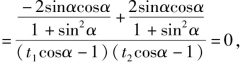
即kMA=-kMB.∴∠OMA=∠OMB.
证法五 (利用椭圆的第二定义证明)
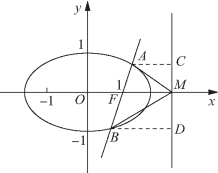
图3-12
不难发现点M是椭圆的右准线x=2与x轴的交点，所以可以运用椭圆的第二定义来证明.
当直线l与x轴重合时，∠OMA=∠OMB=0°，
当直线l与x轴不重合时，如图3-12所示，过点A，B分别作准线x=2的垂线，垂足分别为C，D，则有AC∥BD∥x轴.(www.xing528.com)
由椭圆的第二定义，有
得
即
由AC∥BD∥x轴，有
即
于是
且∠ACM=∠BDM=90°，
可得∠AMC=∠BMD，即有∠AMO=∠BMO.
证法六 (转化为在极坐标平面内证明)
椭圆
若以右焦点为极点，x轴的正方向为极轴，则椭圆C的极坐标方程为
设A(ρ1，θ)，B(ρ2，θ+π).
∴
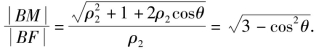
由角平分线定理知，命题得证.
例2 (2015年高考数学全国卷Ⅰ理科第20题)
在直角坐标系xOy中，曲线
与直线l：y=kx+a(a>0)交于M，N两点.
(1)当k=0时，分别求C在点M和N处的切线方程；
(2)y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？请说明理由.
解题策略 在上例的分析中，对这两道高考题的异同进行了比较，实质上，2018年全国Ⅰ卷第19题可以说是本题的变式训练，本题的难点在第(2)问，以探索存在性问题的形式出现，同上例类似，把探究角相等问题转化为对斜率之间关系的探究，方法也很多.总体上通过对直线与抛物线位置关系的讨论运用方程理论求解，若能结合角平分线分线段成比例定理或曲线上点的对称特点，可产生意想不到的效果，若通过平面向量的数量积来探究∠OPM=∠OPN，是发散思维引出的奇妙解法.
解：(1)由题设可得
或
又
故
在
处的导数值为
在点
处的切线方程为
即
在
处的导数值为
在点
处的切线方程为
即
故所求切线方程为
和
(2)解法一 (常规解法：探究存在点P使∠OPM=∠OPN转化为kPM+kPN=0)
存在符合题意的点，证明如下：
设P(0，b)为符合题意的点，M(x1，y1)，N(x2，y2)，直线PM，PN的斜率分别为k1，k2.
将y=kx+a代入C的方程得x2-4kx-4a=0，故x1+x2=4k，x1x2=-4a.
从而
当b=-a时，有k1+k2=0，则直线PM的倾斜角与直线PN的倾斜角互补.
故∠OPM=∠OPN，∴点P(0，-a)符合题意.
解法二 (利用角平分线分线段成比例定理进行探究)
设MN与y轴交于点A，设
将y=kx+a代入
得到x2-4kx-4a=0，由根与系数的关系得x1+x2=4k，x1x2=-4a.
假设存在点P(0，b)，使得当k变动时，总有∠OPM=∠OPN，
则由角平分线分线段成比例定理得
即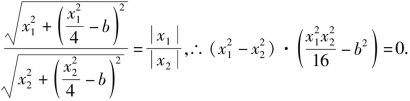
∵k是变化的，
不会恒等于0，因此
当b=a时，唯有k=0时成立，∴b=-a，y轴上存在点P(0，-a)，使得当k变动时，总有∠OPM=∠OPN.
图3-13
解法三 (利用对称点进行探索)
如图3-13所示，设点
则
得直线MN的方程为
令x=0，得
由∠OPM=∠OPN得点M关于y轴的对称点
在直线NP上，
直线NM1的方程为
令x=0，得到P点的纵坐标
为定值-a，
∴存在点P(0，-a)，使得∠OPM=∠OPN.
解法四 (利用平面向量数量积进行探索)
设P(0，b)符合题意，M(x1，y1)、N(x2，y2).
当k≠0时，有x1+x2≠0，将y=kx+a代入C的方程得x2-4kx-4a=0，故x1+x2=4k，x1x2=-4a.
又
则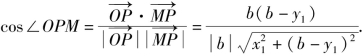
同理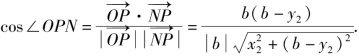
若cos∠OPM=cos∠OPN，有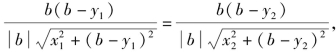
即
化简得b2=a2，即b=-a或b=a(舍去)，
从而b=-a时，有cos∠OPM=cos∠OPN，即∠OPM=∠OPN.
当k=0时，若b=-a，则∠OPM=∠OPN.
综上，点P(0，-a)符合题意.
二、发散训练
(2018年高考数学上海卷第20题)设常数t>2，在平面直角坐标系xOy中，已知点F(2，0)，直线l：x=t，曲线Γ：y2=8x(0≤x≤t，y≥0)，l与x轴交于点A，与Γ交于点B，P、Q分别是曲线Γ与线段AB上的动点.
(1)用t表示点B到点F的距离；
(2)设t=3，|FQ|=2，线段OQ的中点在直线FP上，求△AQP的面积；
(3)设t=8，是否存在以FP、FQ为邻边的矩形FPEQ，使得点E在Γ上？若存在，求点P的坐标;若不存在，说明理由.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
