数列背景下的探索性与新颖性问题解析

以数列为背景的探索性问题和数列新情景题的不断涌现为我们提供了实现知识拓展与创新能力提升的新领域，是数学学习中的一块宝藏，特别是新定义型数列及其性质的研究在近年来的高考命题中时有出现，对数列的函数特征的挖掘更加深入，与不等式知识的综合更加紧密，突出考查考生对知识的融会贯通能力及转化与化归能力.

一、例题精讲

例1　如果有穷数列a1，a2，a3，…，am(m为正整数)满足条件：

a1=am，a2=am-1，…，am=a1，即ai=am-i+1(i=1，2，…，m)我们称其为“对称数列”.

例如，数列1，2，5，2，1与数列8，4，2，2，4，8都是“对称数列”.

(1)设{bn}是7项的“对称数列”，其中b1，b2，b3，b4是等差数列，且b1=2，b4=11，依次写出{bn}的每一项；

(2)设{cn}是49项的“对称数列”，其中c25，c26，…，c49是首项为1，公比为2的等比数列，求{cn}各项的和S；

(3)设{dn}是100项的“对称数列”，其中d51，d52，…，d100是首项为2，公差为3的等差数列，求{dn}的前n项和Sn(n=1，2，…，100).

解题策略　等差数列和等比数列是数列的两个最基本的模型，这是高考中的热点之一，然而命题中常常把这两个最基本的模型进行组合得到数列的一些新概念、新定义，如等和数列、等差比数列以及本题中的对称数列等.又如2018年高考数学上海卷定义了两个数列接近的概念，实际上这类问题并不是难题，关键是要“吃透”新概念的含义以及与已学知识的关系，化新为旧，解题过程中运用的数学工具肯定是我们熟知的.

解：(1)设数列{bn}的公差为d，则b4=b1+3d=2+3d=11，解得d=3，

∴数列{bn}为2，5，8，11，8，5，2.

(2)S=c1+c2+…+c49=2(c25+c26+…+c49)-c25

=2(1+2+22+…+224)-1=2(225-1)-1=226-3=67108861.

(3)d51=2，d100=2+3×(50-1)=149.

由题意得d1，d2，…，d50是首项为149，公差为-3的等差数列.

当n≤50时，

当51≤n≤100时，Sn=d1+d2+…+dn=S50+(d51+d52+…+dn)

综上所述，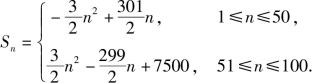

例2　由函数y=f(x)确定数列{an}，an=f(n)，函数y=f(x)的反函数y=f-1(x)能确定数列{bn}，bn=f-1(n)，若对于任意n∈N*，都有bn=an，则称数列{bn}是数列{an}的“自反数列”.

(1)若函数确定数列{an}的自反数列为{bn}，求an；(www.xing528.com)

(2)已知正数数列{cn}的前n项和写出Sn的表达式，并证明你的结论；

(3)在(1)和(2)的条件下，d1=2，当n≥2时，设是数列{dn}的前n项和，且Dn>loga(1-2a)恒成立，求a的取值范围.

解题策略　第(1)小题由函数与反函数的概念引申出“自反数列”这一新概念，一个数列的“自反数列”即本身，从而可以求得参数值，确定an；第(2)小题的求解可由递推公式实施累加的方法；第(3)小题的求解可运用裂项相消法求和，在求得Dn之后，由于Dn>loga(1-2a)恒成立，即loga(1-2a)<(Dn)min，再通过解不等式求得a的取值范围.

解：(1)由题意得即

(2)∵正数数列{an}的前n项和

解之得c1=1，S1=1.

当n≥2时，

即累加得

(3)在(1)和(2)的条件下，d1=2，当n≥2时，设

由Dn是数列{dn}的前n项的和，有

∵Dn>loga(1-2a)恒成立，即loga(1-2a)恒小于Dn的最小值，

显然Dn的最小值在n=1时取得，即(Dn)min=2.

∴loga(1-2a)<2，即1-2a>解得

二、发散训练

(2018年高考数学上海卷第21题)给定无穷数列{an}，若无穷数列{bn}满足：对任意n∈N*，都有|bn-an|≤1，则称{bn}与{an}“接近”.

(1)设{an}是首项为1，公比为的等比数列，bn=an+1+1，n∈N*，判断数列{bn}是否与{an}接近？并说明理由；

(2)设数列{an}的前4项为：a1=1，a2=2，a3=4，a4=8，{bn}是一个与{an}接近的数列，记集合M={x|x=bi，i=1，2，3，4}，求M中元素的个数m；

(3)已知{an}是公差为d的等差数列，若存在数列{bn}满足：{bn}与{an}接近，且在b2-b1，b3-b2，…，b201-b200中至少有100个为正数，求d的取值范围.