李正兴高中数学微专题：点列问题解题策略与数列与解析几何的交汇

数列与解析几何知识的交汇与综合是高考命题的又一个热点，可以充分体现对数学解题能力即核心素养的考查，其表现形式是点列问题，通常方程曲线上的点的横坐标、纵坐标分别是某两个不同数列的项，而这两个数列又由点所在的曲线建立了联系，从而数列的代数特征与曲线的几何性质紧密相关，这类问题，解析几何知识往往是个载体，核心还是数列问题，下面举几道典型的例题与读者分享.

一、例题精讲

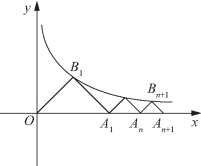
图3-10

例1　如图3-10所示，已知B1，B2，B3，…顺次为曲线上的点，A1，A2，A3，…顺次为x轴上的点，且△OB1A1，△A1B2A2，…，△AnBn+1An+1，…均为等腰直角三角形，其中B1，B2，B3，…均为直角的顶点，记An的坐标为(xn，0)，n∈N*.

(1)求数列{xn}的通项公式；

(2)设Sn为数列的前n项的和，试比较的大小.

解题策略　本例是点列、曲线、等腰直角三角形、数列的求和、数列不等式、数学归纳法、函数的单调性以及放缩法证明不等式等多个知识与方法的综合.解法灵活又精彩，解题的切入口是利用等腰直角三角形的性质或利用直线与曲线的交点得到xn与xn-1的递推关系，而能解到最后的关键是推理证明.在运用数学归纳法证明时要抓住两个步骤，做到“递推基础不可少，归纳假设要用到，结论写明莫忘掉”.

解：(1)解法一　由题设可得点B1(1，1)，A1(2，0)，因此x1=2，

由及△AnBn+1An+1是等腰直角三角形，可知

∴数列是以22=4为首项，4为公差的等差数列.

即

解法二　由题设可得点B1(1，1)，A1(2，0)，lAnBn+1:y=x-xn.

解方程组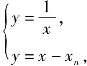得为Bn+1的横坐标，

于是即

∴数列是以22=4为首项，4为公差的等差数列.

即

(2)解法一

下面用数学归纳法证明　①

1当n=1时，时，不等式①成立；

2假设n=k时，不等式①成立，即

那么，当n=k+1时，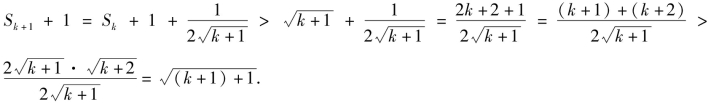

则n=k+1时，不等式①成立.

即对所有n∈N*，不等式①成立，从而有

解法二

从而有

例2　已知点B1(1，y1)，B2(2，y2)，…，Bn(n，yn)，…(n∈N*)顺次为直线上的点，点A1(x1，0)，A2(x2，0)，…，An(xn，0)，…(n∈N*)顺次为x轴上的点，其中x1=a(0<a<1)，对任意n∈N*，点An，Bn，An+1构成以Bn为顶点的等腰三角形.(www.xing528.com)

(1)求数列{yn}的通项公式，并证明它是等差数列；

(2)求证：xn+2-xn是常数，并求数列{xn}的通项公式；

(3)上述等腰三角形AnBnAn+1中是否可能存在直角三角形？若可能，求出此时a的值；若不能，请说明理由.

解题策略　点列问题通常是数列与解析几何知识的交汇与综合，一个点的横坐标、纵坐标分别是某两个不同数列的项，而这两个数列又由点所在的曲线建立了联系，从而数列的代数特征与曲线的几何性质紧密相关，B1(1,y1),B2(2,y2),…,Bn(n，yn)(n∈N*)顺次为直线上的点，则{yn}成等差数列是显然的了.由△AnBnAn+1为等腰三角形，易得xn+2-xn=2，则数列{xn}必定奇数项、偶数项分别成为两个不同的等差数列，所以分奇数、偶数进行讨论，{xn}的通项为分段形式也是必然的.而第(3)问是探索存在性问题，既要全面考察，又要从数与形的两个角度深入探究，把一切可能存在的a值找出来.

解：(1)证明　由题设得又数列{yn}是等差数列.

(2)证明　由题设得=n，∴xn+xn+1=2n,　①

又xn+2+xn+1=2(n+1)，　②

由②-①得xn+2-xn=2.

∴x1，x3，x5，…；x2，x4，x6，…分别都是等差数列.

x2n-1=x1+2(n-1)=2n+a-2，x2n=x2+2(n-1)

=2-a+2(n-1)=2n-a.

(3)当n为奇数时，有An(n+a-1，0)，An+1(n+1-a，0).∴|AnAn+1|=2(1-a)；

当n为偶数时，有An(n-a，0)，An+1(n+a，0).∴|AnAn+1|=2a.

作BnCn⊥x轴于Cn，则

要使等腰三角形AnBnAn+1为直角三角形，必须且只需|AnAn+1|=2|BnCn|.

当n为奇数时，有即12a=11-3n.　③

当n=1时，当n=3时，当n≥5时，∵0<a<1，方程③无解;

当n为偶数时，有12a=3n+1.　④

同理可求得n=2时，时，方程④无解.

综上所述，上述等腰三角形AnBnAn+1中可能存在直角三角形，此时a的值为或或

二、发散训练

如图3-11所示，直线与相交于点P，直线l1与x轴交于点P1，过点P1作x轴的垂线交直线l2于点Q1，过点Q1作y轴的垂线交直线l1于点P2，过点P2作x轴的垂线交直线l2于点Q2，…，这样一直作下去，可得到一系列点P1，Q1，P2，Q2，…，点Pn(n=1，2，…)的横坐标构成数列{xn}.

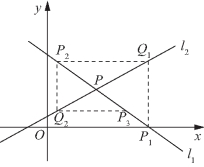
图3-11

(1)证明：

(2)求数列{xn}的通项公式；

(3)比较2与4k2+5的大小.