高中数学微专题———数列性质及应用

以等差与等比数列的知识和规律为主体内容设计的综合试题是高考数列压轴题命制的一个热点，必须重视这两类数列的性质在解题中的应用，特别是性质中的一些对偶关系，可以给解题带来方便，下面把等差数列、等比数列的重要性质归纳如下，读者可以对照看看.

1.等差数列的重要性质

(1)在等差数列{an}中，任意两项an，am之间的关系为an=am+(n-m)d(m，n∈N*)

(2)在等差数列{an}中，当m+n=p+q(m、n、p、q∈N*)时，则有am+an=ap+aq;特别地，当m+n=2p时，则有am+an=2ap.

(3)若数列{an}是公差为d的等差数列，则数列{λan+b}(λ，b是常数)是公差为λd的等差数列；若数列{an}，{bn}分别是公差为d，m的等差数列，则{λ1an+λ2bn}(λ1，λ2是常数)是公差为λ1d+λ2m的等差数列.

(4)数列{an}是公差为d的等差数列，每隔k(k∈N*)项取出一项得到的ak，ak+m，ak+2m仍为等差数列，公差为md.

(5)等差数列前n项和是关于n的二次函数且常数项为0.

(6)在等差数列{an}中，前n项和为Sn，若项数为2n(n∈N*)，则若项数为2n+1(n∈N*)，则

(7)在等差数列{an}中，数列Sn，S2n-Sn，S3n-S2n，…成等差数列.

2.等比数列的重要性质

(1)在等比数列{an}中，任意两项an、am之间的关系为an=amqn-m(m、n∈N*).

(2)在等比数列{an}中，若m+n=p+q(m、n、p、q∈N*)，则aman=apaq;特别地，当m+n=2p时，则有

(3)若数列{an}是公比为q的等比数列，则数列{λan}(λ是常数)是公比为q的等比数列；若数列{an}，{bn}分别是公比为q，m的等比数列，则{anbn}是公比为qm的等比数列.

(4)数列{an}是公比为q的等比数列，每隔k(k∈N*)项取出一项得到的ak，ak+m，ak+2m仍为等比数列，公比为qm.

(5)等比数列前n项和系数和常数项是互为相反数的类指数函数，底数为公比q.

(6)在等比数列{an}中，前n项和为Sn，若项数为2n(n∈N*)，则

(7)在等比数列{an}中，若Sm≠0，则数列Sm，S2m-Sm，S3m-S2m，…成等比数列.

3.等差、等比数列的综合问题

创新题型是高考命题的热点，数列又是创新题型的热点.近年来由等差、等比数列通过组合、类比或推广构造出一种新的数列，如等和数列、等积数列、等方比数列、积等差数列、商等差数列等，我们称之为由这两类基本数列演化出来的“生成数列”，解题的关键仍然是运用等差、等比数列知识解题，涉及哪个数列问题就灵活地运用相关知识特别是上述重要性质来解决.

一、例题精讲

例1　(2017年高考数学山东卷文科第19题)

已知{an}是各项均为正数的等比数列，且a1+a2=6，a1a2=a3.

(1)求数列{an}的通项公式；

(2){bn}为各项非零的等差数列，其前n项和为Sn，已知S2n+1=bnbn+1，求数列的前n项和Tn.

解题策略　数列在高考中的地位是比较重要的，其中数列的通项公式与前n项和的求解方法是数列的核心问题，命题的重点为等差数列和等比数列的通项公式、前n项和公式以及常见数列的求和方法.第(1)问，根据条件列出关于首项a1和公比q的方程组，求出首项a1和公比q，从而得到数列{an}的通项公式；第(2)问，解题的关键是写出{bn}的通项公式，观察的特点是等差×等比的形式，采用错位相减法是首选，也可考虑构造特殊数列的方法或裂项相消法求和,而采用导数法则属妙思巧解.

解：(1)设{an}的公比为q，由题意知：又an>0,

解得a1=2，q=2.∴an=2n.

(2)解法一　(错位相减法)　由题意知：又S2n+1=bnbn+1，bn+1≠0，∴bn=2n+1，令则因此

又

两式相减得

解法二　(构造法)　同解法一得

又　①

设即　②

比较①②得解得为常数列.

则

故

解法三　(裂项相消法)

∴Tn=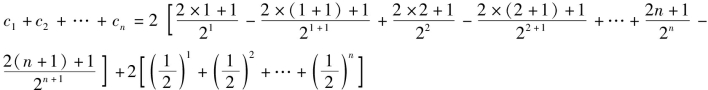

解法四　(拆项并运用导数法)　由解法一得

∴Tn

令则

再将x换成得

例2　在数列{an}与{bn}中，a1=1，b1=4.数列{an}的前n项和{Sn}满足：nSn+1-(n+3)Sn=0，2an+1为bn与bn+1的等比中项，n∈Z+.

(1)求a2，b2的值；(www.xing528.com)

(2)求数列{an}与{bn}的通项公式.

解题策略　本例以等差等比两种基本数列为载体，考查数列的通项以及通项与前n项和的关系.第(1)问比较简单，可直接求解;第(2)问可以在第(1)问的基础上继续运用归纳—猜想—证明的解题方法，也可以从条件nSn+1-(n+3)Sn=0出发利用通项与前n项和的关系转化为研究数列{an}，探求其通项，或先求出和数列{Sn}的通项再通过an=Sn-Sn-1求{an}的通项并结合其他条件求{bn}的通项.

解：(1)由题设有a1+a2-4a1=0，a1=1，解得a2=3，

由题设又有解得b2=9.

(2)解法一　(归纳—猜想—证明)　由题设nSn+1-(n+3)Sn=0，

a1=1，b1=4及a2=3，b2=9，进一步可得a3=6，b3=16，a4=10，b4=25，

由此猜想

先证

当n=1时，等式成立.

当n≥2时用数学归纳法证明如下：

1当n=2时，等式成立；

2假设当n=k时等式成立，即

由题设有

①式减②式整理得kak+1=(k+2)ak，从而有

这就是说，当n=k+1时等式也成立，根据 12 可知，等式对任何的n≥2成立.

综上所述，等式对任何的n∈Z+都成立.

再用数学归纳法证明bn=(n+1)2，n∈Z+.

3当n=1时，b1=(1+1)2，等式成立.

4假设当n=k时等式成立，即bk=(k+1)2，那么

也就是说，当n=k+1时等式也成立，根据 34 可知，等式bn=(n+1)2对任何n∈Z+都成立.

解法二　(由和数列{Sn}递推式求an)　由题设可知

①式减②式，整理得nan+1=(n+2)an，n≥2，

∴2a3=4a2，3a4=5a3，…，(n-1)an=(n+1)an-1，n≥3.

将以上各式左右两端分别相乘，得

由(1)并化简得　③

③式对n=1，2也成立.

由题设有即

令则xnxn+1=1，即由x1=1得xn=1，n≥2.

即bn=(n+1)2，n≥1.

解法三　(先求Sn再求an)　由题设有nSn+1=(n+3)Sn，n∈Z+，

∴S2=4S1，2S3=5S2，…，(n-1)Sn=(n+2)Sn-1(n≥2)，

将以上各式左右两端分别相乘，得

1·2·…·(n-1)Sn=4·5·…·(n+2)S1.

化简得

由(1)，上式对n=1，2也成立，

上式对n=1也成立.

以下同解法二，可得bn=(n+1)2，n≥1.

二、发散训练

1. 设数列{an}、{bn}满足an=4n+1，bn=3n，令{cn}是由数列{an}、{bn}中的公共项按照从小到大顺序排列而成的数列，求数列{cn}的通项公式.

2. 已知数列{an}的前n项和Sn=3n2+8n，{bn}是等差数列，且an=bn+bn+1.

(1)求数列{bn}的通项公式；

(2)令求数列{cn}的前n项和Tn.