高考中经常出现新定义的具有某种特殊性质的函数,提出若干需要解决的问题,由于不是数学学习中出现过的常见函数,往往给人以陌生的感觉,这类新情景题旨在考查学生当场理解并加以运用的能力.还有一些考题,虽然题设中给出的函数是常见函数的组合,由于其形态特殊,具有新颖的特点,如指数函数与一次或二次函数的联袂型,对数函数与一次或二次函数的联袂型,不是常规解法就能解决的,本讲通过实例讲解用导数作为解题工具研究和解决这些新颖性问题.
一、例题精讲
例1 (2018年高考数学江苏卷理科第19题)
记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.
(1)证明:函数f(x)=x与g(x)=x2+2x-2不存在“S点”;
(2)若函数f(x)=ax2-1与g(x)=lnx存在“S点”,求实数a的值;
解题策略 本题给出了“S点”的新定义,主要考查利用导数研究初等函数的性质以及探索存在性问题,考查综合运用数学思想方法分析与解决问题的能力和逻辑推理能力.第(1)问,利用“S点”的定义证明即相应方程组是否有解即可;第(2)问,利用新定义建立方程组求解;第(3)问,利用函数的零点及新定义求解.
解:(1)证明 函数f(x)=x,g(x)=x2+2x-2,则f′(x)=1,g′(x)=2x+2.
由f(x)=g(x)且f′(x)=g′(x),得![]() 此方程组无解,
此方程组无解,
因此,f(x)与g(x)不存在“S点”.
(2)函数f(x)=ax2-1,g(x)=lnx,则![]()
设x0为f(x)与g(x)的“S点”,由f(x0)=g(x0)且f′(x0)=g′(x0),得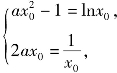 即
即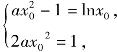 ①
①
解得![]() 即
即![]() 则
则![]()
当![]() 时,
时,![]() 满足方程组①,即x0为f(x)与g(x)的“S点”,因此,a的值为
满足方程组①,即x0为f(x)与g(x)的“S点”,因此,a的值为![]()
(3)对任意a>0,设h(x)=x3-3x2-ax+a.
∵h(0)=a>0,h(1)=1-3-a+a=-2<0,且h(x)的图像是不间断的,
∴存在x0∈(0,1),使得h(x0)=0,令![]() 则b>0.
则b>0.
函数![]() 则
则![]()
由f(x)=g(x)且f′(x)=g′(x),得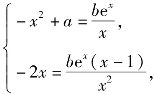
即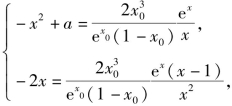 ②
②
此时,x0满足方程组②,即x0是函数f(x)与g(x)在区间(0,1)内的一个“S点”.因此,对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”.
例2 (2018年高考数学全国卷Ⅲ理科第21题)
已知函数f(x)=(2+x+ax2)ln(1+x)-2x.
(1)若a=0,证明:当-1<x<0时,f(x)<0;当x>0时,f(x)>0;
(2)若x=0是f(x)的极大值点,求a.(https://www.xing528.com)
解题策略 本题是对数函数与一次或二次函数的联袂型,主要考查导数在研究不等式问题与极值问题中的应用,考查化归与转化思想、分类讨论思想与数形结合思想的综合应用,考查的核心素养是数学抽象、数学运算.第(1)问,通过求导研究函数的单调性即可证明;第(2)问,根据函数取得极值的条件,建立关于a的式子求解.一般而言,利用导数解决不等式问题主要是通过研究函数的单调性求出函数的极值或最值,并利用最值解决相关的不等式问题.
解:(1)证明 当a=0时,![]()
设函数![]() 则
则![]()
当-1<x<0时,g′(x)<0;当x>0时,g′(x)>0.
故当x>-1时,g(x)≥g(0)=0.
且仅当x=0时,g(x)=0,从而f′(x)≥0,且仅当x=0时,f′(x)=0,
∴f(x)在(-1,+∞)单调递增.
又f(0)=0,故当-1<x<0时,f(x)<0;当x>0时,f(x)>0.
(2)若a≥0,由(1)知,当x>0时,f(x)≥(2+x)ln(1+x)-2x>0=f(0),这与x=0是f(x)的极大值点矛盾.
若a<0,设函数![]()
由于当![]() 时,2+x+ax2>0,故h(x)与f(x)符号相同.
时,2+x+ax2>0,故h(x)与f(x)符号相同.
又h(0)=f(0)=0,故x=0是f(x)的极大值点,当且仅当x=0是h(x)的极大值点.
如果6a+1>0,则当![]() 且
且![]() 时,h′(x)>0,
时,h′(x)>0,
故x=0不是h(x)的极大值点.
如果6a+1<0,则a2x2+4ax+6a+1=0存在根x1<0,故当x∈(x1,0),且![]() 时,h′(x)<0,∴x=0不是h(x)的极大值点.
时,h′(x)<0,∴x=0不是h(x)的极大值点.
如果6a+1=0,则![]() 则当x∈(-1,0)时,h′(x)>0,当x∈(0,1)时,h′(x)<0,∴x=0是h(x)的极大值点,从而x=0是f(x)的极大值点.
则当x∈(-1,0)时,h′(x)>0,当x∈(0,1)时,h′(x)<0,∴x=0是h(x)的极大值点,从而x=0是f(x)的极大值点.
综上,![]()
二、发散训练
若函数f(x)在(0,+∞)上恒有xf′(x)>f(x)成立(其中f′(x)为f(x)的导函数),则称这类函数为A类函数.
(1)若函数g(x)=x2-1,试判断g(x)是否为A类函数;
(2)若函数![]() 是A类函数,求函数h(x)的单调区间;
是A类函数,求函数h(x)的单调区间;
(3)若函数f(x)是A类函数,当x1>0,x2>0时,证明:f(x1)+f(x2)>f(x1+x2).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




