高中数学微专题：函数、不等式问题导数研究及证明

函数背景下的不等式证明是个难点，面临两个方面的挑战：一是其基本方法是构造函数法，要善于观察待证不等式的等价不等式的结构特征去构造出相应的、适当的、合理的函数，将不等式证明的问题转化为对函数有关性质的研究的问题；二是要掌握有关函数性质的知识，掌握对有关函数性质研究的方法，特别是导数法，积累对有关函数性质研究的经验.

函数不等式的形式通常为f(x)≥g(x).证明方法如下：

(1)构造函数H(x)=f(x)-g(x)，确定函数的定义域后，通过求导数H′(x)，求出H(x)的最小值(或极小值)；

(2)说明函数H(x)的最小值(或极小值)为非负数即可.

另一种证法是把待证不等式等价转化为f(x)≥g(x)型，由此构造两个函数h(x)=f(x)，u(x)=g(x)，接下来的工作是利用导数判断h(x)，u(x)的单调性，进而求出函数h(x)，u(x)的最值或临界值.

一、例题精讲

例1　(2018年高考数学全国卷Ⅲ文科第21题)

已知函数

(1)求曲线y=f(x)在点(0，-1)处的切线方程；

(2)证明：当a≥1时，f(x)+e≥0.

解题策略　本题主要考查导数的几何意义，利用导数证明不等式，考查的数学核心素养是逻辑推理、数学运算.第(1)问，首先求出导函数f′(x)，然后将x=0代入，得切线的斜率，从而求出切线方程；第(2)问，利用放缩法进行转化，构造函数，判断单调性，求最值，即可完成证明.当然，不等式证明的关键是合理放缩，可降低难度，不等式证明的放缩技巧性强，要熟悉常见的几种函数放缩模型：ex≥x+1;x-1≥lnx;x≥sinx(x≥0)，选择恰当的放缩模型，对函数进行转化、变形，构造新函数，判断新函数的单调性，求出最值，这其中，运用导数研究和证明函数的单调性是证明的核心步骤.

解：(1)

因此曲线y=f(x)在(0，-1)处的切线方程是2x-y-1=0.

(2)证法一　当a≥1时，f(x)+e≥(x2+x-1+ex+1)ex.

令g(x)=x2+x-1+ex+1，则g′(x)=2x+1+ex+1.

当x<-1时，g′(x)<0，g(x)单调递减；

当x>-1时，g′(x)>0，g(x)单调递增；

∴g(x)≥g(-1)=0，因此f(x)+e≥0.

证法二　函数y=f(x)的定义域为

当a≥1时，令f′(x)=0，得x=2或其中

则函数y=f(x)的单调递减区间为单调递增区间为

又当x∈(2，+∞)时，f(x)>0恒成立，

故

故当a≥1时，f(x)+e≥0.

证法三　不等式f(x)+e≥0等价于ax2+x-1+ex+1≥0.

∵ex≥x+1，∴ax2+x-1+ex+1≥ax2+x-1+1+(x+1)=ax2+2x+1.

当a≥1时，ax2+2x+1≥x2+2x+1=(x+1)2≥0，即结论得证.

例2　已知函数

(1)设函数F(x)=18f(x)-x2，求F(x)的单调区间与极值；

(2)设a∈R，解关于x的方程

(3)设n∈N*，证明：

解题策略　本例是一道有众多知识相交汇的综合题，主要考查函数导数的应用、不等式的证明、解方程等基础知识、考查数形结合、函数与方程、分类与整合等数学思想方法以及推理运算、分析问题、解决问题的能力，其中(1)是容易题；对于(2)，必须对参数a进行讨论；对于(3)，含字母的式子较为复杂，运算变形要仔细.

解：(1)F(x)=18f(x)-x2=-x3+12x+9(x≥0)，∴F′(x)=-3x2+12.

令F′(x)=0，得x=2(x=-2舍去).

当x∈=[0，2)时，F′(x)>0；x∈(2，+∞)时，F′(x)<0,

即当x∈[0，2)时，F(x)为增函数；当x∈[2，+∞)时，F(x)为减函数.

x=2为F(x)的极大值点，F(2)=-8+24+9=25.

(2)原方程变为

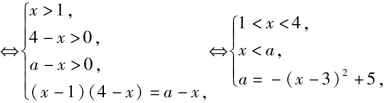如图3-8所示.

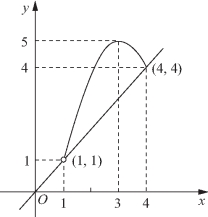
图3-8

当1<a≤4时，原方程有一解

当4<a<5时，原方程有两解

当a=5时，原方程有一解x=3;

当a≤1或a>5时，原方程无解.

(3)证明　由已知得

设数列{an}的前n项和为Sn，且从而有a1=S1=1，

当k≥2时，

又(www.xing528.com)

即对任意的k≥2，有

又

∴Sn≥h(1)+h(2)+…+h(n)，故原不等式成立.

例3　已知f(x)是定义在R上的奇函数，且当x<0时，f(x)单调递增，f(-1)=0，设φ(x)=sin2x+mcosx-2m，集合求M∩N.

解题策略　本例是2011年清华大学原自主招生数学试题，把函数性质、三角知识与集合运算融为一体，有考查学生数学基础知识及解题能力的功能，求解本题的关键是转化，转化为含参数一元二次不等式在区间上的恒成立问题，再转化为函数问题，运用函数与方程的思想方法求解，然而分类讨论的步骤较多，显然繁杂，若运用导数解则简捷多了.

解：f(x)是定义在R上的奇函数，且当x<0时，f(x)单调递增，f(-1)=0，∴当x>0时，f(x)也单调递增，且f(1)=0，于是f(x)<0等价于x<-1或0<x<1.

由φ(x)<-1,得cos2x-mcosx+2m-2>0.

令t=cosx，则0≤t≤1，于是问题等价转化为：

当不等式t2-mt+2m-2>0在t∈[0，1]上恒成立时，求实数m的取值范围.

由t2-mt+2m-2>0(0≤t≤1),得

设则令h′(t)=0，

解得舍去).

当时，h′(t)>0，h(t)为增函数；

当时，h′(t)<0，h(t)为减函数，

当时，h(t)取得[0，1]上的最大值

故

例4　已知函数f(x)=(2-a)x-2ln(1+x)(0<a<2).

(1)讨论函数f(x)的单调性；

(2)设g(x)=x2+4x+a,若对任意x1∈[0,3]，存在x2∈[0,3],使g(x1)≥f(x2)成立，求实数a的取值范围；

(3)求证：且n≥2).

解题策略　本例的难点在第(2)问，对任意x1∈[0,3]，存在x2∈[0,3]使g(x1)≥f(x2)能成立.其实质是g(x)min≥f(x)min,从而求出参数a的取值范围.

如果改变一下命题：对定义域D=[a,b]，g(x)≥f(x)恒成立.则实质是对任意x∈[a,b]，g(x)min≥f(x)max,当然两者都可以用导数解决.读者必须注意这其中能成立与恒成立之间的差异以及处理问题方法上的差异.

解：(1)由题意，得

由于当0<a<2时，

∴当时，f′(x)<0;当时,f′(x)>0,

∴f(x)在区间上为减函数，在区间上为增函数.

(2)由(1)知，当即时，f(x)在区间上为减函数，在区间上为增函数，

∴此时f(x)在区间[0,3]上的最小值为

当即时，f(x)在区间[0,3]上为减函数,

∴此时f(x)在区间[0，3]上的最小值为f(x)min=f(3)=6-3a-4ln2.

又g(x)=x2+4x+a=(x+2)2+a-4在区间[0,3]上的最小值为g(x)min=g(0)=a,

由题设对任意x1∈[0,3]，存在x2∈[0,3]，使g(x1)=f(x2)成立，知

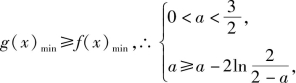或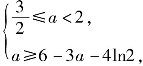

解得0<a<2,故a的取值范围为(0,2).

(3)证明　当a=1时，f(x)=x-2ln(1+x).

由(1)知，f(x)在区间(-1,1)上为减函数，

∴当n∈N且n≥2时，即

∴当n∈N,且n≥2时，即

令n=2,3,4,…,得不等式

将上述不等式左右两边分别相加得，

二、发散训练

已知函数

(1)求f(x)的单调区间；

(2)若f(x)的最小值为0，求实数a的值；

(3)在(2)的条件下，数列{an}满足a1=1，an+1=f(an)+2.记[x]表示不超过x的最大整数，求[a1]+[a2]+…+[an].