用导数解决函数零点问题

一、函数的零点

1.函数零点的意义

函数y=f(x)的零点就是方程f(x)=0的实数根，亦即函数y=f(x)的图像与x轴交点的横坐标.方程f(x)=0有实数根⟺y=f(x)的图像与x轴有交点⟺函数y=f(x)有零点.

2.函数零点的求法

(1)代数法：求方程f(x)=0的实数根.

(2)导数法：求函数y=f(x)的导数f′(x)，解方程f′(x)=0求得零点.

(3)几何法：利用函数y=f(x)的图像结合函数的性质找出零点.

3.勘根定理

如果函数y=f(x)在区间(a，b)上的图像是连续不断的一条曲线，并且有f(a)f(b)<0，那么，函数y=f(x)在区间(a，b)内有零点，即存在c∈(a，b)，使f(c)=0，这个c也就是方程f(x)=0的根.

4.函数零点问题的题型

函数零点问题的题型主要有：

①确定函数零点所在的区间；②判断函数零点个数；③由函数零点的存在情况求参数的取值范围.

本讲主要讲高次函数与复合函数的零点的探求，以导数为工具研究和解决这类函数的零点问题,进而研究两函数的交点问题，重点是函数与方程之间的转换.方程转换为函数问题，以导数探究函数的单调性、值域、极值、图像等知识解决，两函数交点转化为方程问题可直接求解，也可重新整理后再转化为新的函数问题.高考压轴题中的零点问题往往不是单一的，常常涉及方方面面，综合性强,有一定的难度，是近年高考压轴题命制的热点之一.

一、例题精讲

例1　(2018年高考数学全国卷Ⅱ理科第21题)

已知函数f(x)=ex-ax2.

(1)若a=1，证明：当x≥0时，f(x)≥1；

(2)若f(x)在(0，+∞)只有一个零点，求a.

解题策略　本题主要考查函数的单调性、不等式的证明、函数的零点问题，意在考查学生的推理论证能力、化归与转化能力、运算求解能力，考查的核心素养是逻辑推理、直观想象、数学运算.第(1)问，证明不等式的恒成立问题，可以转化为求函数的最值，比如要证明f(x)≥0，可先求得f(x)的最小值，然后证明这个最小值大于等于0即可.当然在证明过程中，特别是求最值时，这个最小值可能不会明确给出，需利用导数知识求得，本小题首先对不等式进行变换，构造一个新函数，然后利用导数研究新函数的单调性，进而证明不等式.第(2)问，首先也是构造新函数，然后分a≤ 0与a>0两种情况讨论函数的零点个数，且当a>0时，要注意利用导数研究函数的单调性与最值，总之，本题的求解构造新函数很重要，不同的构造可以有不同的解法.

解：(1)证法一　当a=1时，f(x)≥1等价于(x2+1)e-x-1≤0，

设函数g(x)=(x2+1)e-x-1，

则g′(x)=-(x2-2x+1)e-x=-(x-1)2e-x.

当x≠1时，g′(x)<0，∴g(x)在(0，+∞)单调递减.而g(0)=0，故当x≥0时，g(x)≤0，即f(x)≥1.

证法二　当a=1时，f(x)=ex-x2，f′(x)=ex-2x.

令g(x)=ex-2x，g′(x)=ex-2，令g′(x)=0，得x=ln2.

则函数y=g(x)在区间[0，ln2)内单调递减，在区间[ln2，+∞)内单调递增，从而g(x)≥g(ln2)=2-2ln2>0，

∴函数y=f(x)在区间[0，∞)内单调递增，有f(x)≥f(0)=1.

(2)解法一　设函数h(x)=1-ax2e-x.

f(x)在(0，+∞)只有一个零点当且仅当h(x)在(0，+∞)只有一个零点.

当a≤0时，h(x)>0，h(x)没有零点；

当a>0时，h′(x)=ax(x-2)e-x.当x∈(0，2)时，h′(x)<0;当x∈(2，+∞)时，h′(x)>0，∴h(x)在(0，2)单调递减，在(2，+∞)单调递增，故是h(x)在[0，+∞)的最小值.

2若h(2)=0，即在(0，+∞)只有一个零点；

3若h(2)<0，即a>由于h(0)=1，∴h(x)在(0，2)有一个零点.

由(1)知，当x>0时，有一个零点，因此h(x)在(0，+∞)有两个零点.综上，f(x)在(0，+∞)只有一个零点时，

解法二　当x>0时，原问题转化为动直线y=ax与曲线在区间(0，+∞)内只有一个公共点.

由得函数y=h(x)在区间(0，1)内单调递减，在区间(1，+∞)内单调递增.

设y=ax与y=h(x)的一切点为则于是函数y=h(x)在点P处的切线方程为由切线过原点可得x0=2，故

例2　已知f(x)=x3+ax2+b(a，b∈R).

(1)试讨论f(x)的单调性;

(2)若b=c-a(实数c是与a无关的常数)，当函数f(x)有3个不同的零点时，a的取值范围恰好是求c的值.

解题策略　利用导数讨论函数的单调性和极值可以确定函数的零点及零点的分布情况.

解：(1)f′(x)=3x2+2ax，令f′(x)=0，解得当a=0时，

∵f′(x)=3x2>0(x≠0)，∴函数f(x)在(-∞，+∞)上单调递增.(www.xing528.com)

当a>0时，时，时，f′(x)<0.

∴函数f(x)在上单调递增，在上单调递减，

当a<0时，时，时，f′(x)<0.

∴函数f(x)在上单调递增，在上单调递减.

(2)解法一　由(1)知，函数f(x)的两个极值为则函数f(x)有3个零点等价于

从而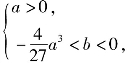　或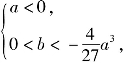　又b=c-a，

∴当a>0时，或a<0时，

设函数f(x)有3个零点时，a的取值范围恰好是(-∞，则在(-∞，-3)上，g(a)<0且在上g(a)>0均成立.

∴g(-3)=c-1≤0且因此c=1.

此时，f(x)=x3+ax2+1-a=(x+1)[x2+(a-1)x+1-a].

∵函数有3个零点，则x2+(a-1)x+1-a=0有两个异于-1的不等实根.

∴Δ=(a-1)2-4(1-a)=a2+2a-3>0且(-1)2-(a-1)+1-a≠0.

解得

综上c=1.

解法二　由(1)知,f(x)的两极值为

函数f(x)有3个不同的零点等价于

即

由题中条件可知，上述关于a的不等式的解集恰好为

则为关于a的方程　　②的解集，从而c可能的取值为

若c=-3，由于a=1不是②式的解，∴②式的解集不等于集合A，故不符合题意.若由于a=1不是②式的解，∴②式的解集也不等于集合A，故不符合题意.若c=1，①式即为也就是其解集恰为故c=1即为所求.

解法三　同解法二，函数f(x)有3个不同的零点等价于

即其解集恰为

又不等式即的解集为

故与同解.

比较两个同解不等式的系数可得c=1.

解法四　由(1)知,f(x)的两极值为

1当a∈(-∞，-3)时，f(0)为极大值，为极小值.

f(x)有3个不同的零点恒成立.

记由

可得当a∈(-∞，-3)时，g′(a)<0，故g(a)在(-∞，-3)上单调递减.

∴g(a)>g(-3)=1，从而-3≤c≤1.

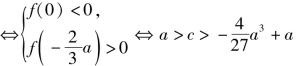2当时，f(0)为极小值，为极大值.f(x)有3个不同的零点恒成立.

由(1)知,当时，故1≥c≥1，即c=1.

综合 12 有c=1，此时，f(x)=x3+ax2+1-a=(x+1)[x2+(a-1)x+1-a]，当f(x)有3个不同的零点时，关于x的方程x2+(a-1)x+1-a=0有两个异于-1的相异实根.

故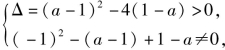　解之得

综上所述，c=1.

二、发散训练

已知函数f(x)=ae2x+(a-2)ex-x.

(1)讨论f(x)的单调性；

(2)若f(x)有两个零点，求a的取值范围.