导数研究函数极值、最值及优化问题:李正兴高中数学微专题

1.用导数研究函数的极值

求可导函数y=f(x)极值的步骤：

(1)确定函数的定义域.

(2)求导数f′(x).

(3)求方程f′(x)=0的根.

(4)检验f′(x)在方程根左右值的符号，求得极值(若左正右负，则f(x)在这个根处取极大值；若左负右正，则f(x)在这个根处取极小值).

2.用导数研究函数的最值

设y=f(x)在[a，b]上连续，在(a，b)内可导，求函数f(x)在[a，b]上的最值的步骤：

(1)求函数在(a，b)内的极值.

(2)求函数在区间端点的函数值f(a)，f(b).

(3)将函数f(x)的各极值与f(a)，f(b)比较，其中最大的一个为最大值，最小的一个为最小值.

3.用导数研究实际应用中的优化问题

(1)利用导数解决实际应用中优化问题的一般步骤：

1)分析实际问题中各量之间的关系，列出实际问题的数学模型，写出实际问题中变量之间的函数关系y=f(x)，并确定其定义域.

2)求函数的导数f′(x)，解方程f′(x)=0.

3)比较函数在区间端点和使f′(x)=0的点数值的大小，最大(小)者为最大(小)值.

(2)解决实际应用中优化问题必须注意以下两点：

1)求实际问题中的最大(小)值，一定要注意实际问题的意义，不符合实际问题的值应舍去.

2)用导数求解实际问题中的最大(小)值时，如果函数在区间内只有一个极值点，就不用与端点值比较，也可以知道该极值点也是最值点.

一、例题精讲

例1　(2017年高考数学全国卷Ⅲ理科第21题)

已知函数f(x)=x-1-alnx.

(1)若f(x)≥0，求a的值；

(2)设m为整数，且对于任意正整数求m的最小值.

解题策略　在函数的所有问题中，函数的单调性是最基础的问题，若含有参数，一般需对参数进行讨论，从而确定函数的单调性，再根据所求进行相应的判断，求解与证明.第(1)问，通过求函数的导数，对函数的单调性进行研究，求解函数的最小值是确定a的值.数列不等式的证明或求解主要有两种思路：①通过函数的单调性得到数列的单调性，从而解决问题；②对数列的不等关系进行放缩，直接证明或求解.第(2)问将问题转化为“和”式不等式，根据数列求和公式求解，其中应灵活运用放缩的技巧.

解：(1)f(x)的定义域为(0，+∞).

若不满足题意；

若a>0，由知，当x∈(0，a)时，f′(x)<0;当x∈(a，+∞)时，f′(x)>0，∴f(x)在(0，a)单调递减，在(a，+∞)单调递增.

故x=a是f(x)在(0，+∞)的唯一最小值点.

由于 f(1)=0,∴当且仅当a=1时，f(x)≥0，故a=1.

(2)解法一　由(1)知,当x∈(1，+∞)时x-1-lnx>0.

令得从而有

故而

当n≥3时，

因此，对任意正整数n，要使恒成立，必须m≥3，∴m的最小值为3.

例2　设函数f(x)=(x-1)ex-kx2(其中k∈R).

(1)当k=1时，求函数f(x)的单调区间；

(2)当时，求函数f(x)在[0，k]上的最大值M.

解题策略　第(1)问，把k=1代入f(x)=(x-1)ex-kx2(k∈R)，对f(x)求导，令f′(x)=0得零点坐标，由f′(x)在定义域子区间的正负，确定f(x)的单调区间.

第(2)问，按照求函数f(x)在[a,b]上的最大值和最小值的步骤进行，由于f(x)含有参数k，且定义域区间为(0,k],k为参变数，必须对k的取值分类讨论，层层深入，攻克难关.

解：(1)当k=1时，f(x)=(x-1)ex-x2，f′(x)=ex+(x-1)ex-2x=xex-2x=x(ex-2)，令f′(x)=0，得x1=0，x2=ln2.

当x变化时，f′(x)、f(x)的变化如下表：(www.xing528.com)

由上表可知，函数f(x)的递减区间为(0，ln2)，递增区间为(-∞，0)和(ln2，+∞).

(2)f′(x)=ex+(x-1)ex-2kx=xex-2kx=x(ex-2k).

令f′(x)=0，得x1=0，x2=ln(2k).

令g(k)=ln(2k)-k，则

∴g(k)在上递增，∴g(k)≤ln2-1=ln2-lne<0.

从而ln(2k)<k，∴ln(2k)∈[0，k].

∴当x∈(0，ln(2k))时，f′(x)<0;当x∈(ln(2k)，+∞)时，f′(x)>0，

M=max{f(0)，f(k)}=max{-1，(k-1)ek-k3}.

令h(k)=(k-1)ek-k3+1，则h′(k)=k(ek-3k).

令φ(k)=ek-3k，则φ′(k)=ek-3≤e-3<0，∴φ(k)在上递减，

而存在使φ(x0)=0，

且当时，φ(k)>0，当k∈(x0，1)时，φ(k)<0.

∴h(k)在上单调递增，在(x0，1)上单调递减.

∴h(k)≥0在上恒成立，当且仅当k=1时取得“=”.

综上，函数f(x)在[0，k]上的最大值M=(k-1)ek-k3.

图3-7

例3　某企业拟建造如图3-7所示的容器(不计厚度，长度单位：米)，其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的容积为立方米，且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为c(c>3)千元，设该容器的建造费用为y千元.

(1)写出y关于r的函数表达式，并求该函数的定义域；

(2)求该容器的建造费用最小时的r.

解题策略　利用导数解决生活中的优化问题的一般步骤求解，具体是：

第一步：分析实际问题中各量之间的关系，求出建造费用y关于圆柱半径r的函数关系式，并求出变量r的取值范围.

第二步：对所求出的函数y=f(r)求导，解方程f′(r)=0,结合函数单调性求函数的极小值.

第三步：对参数进行讨论，确定在参数取不同范围值时的极小值，并比较与函数在定义域区间端点函数值的大小，确定y=f(r)的最小值.

第四步：回归实际问题作答.

在本题的求解过程中，对于(1)，定义域必须优先考虑，不可忽视“l≥2r”的作用；对于(2)，求函数最值，求导后必须对c的取值进行分类讨论，当然本小题还可以结合均值不等式与导数一起考虑.

解：(1)设容器的容积为V，由题意知又

故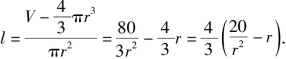由于l≥2r，因此0<r≤2.

所建造费用

因此

(2)解法一　由(1)得,

由于c>3，∴c-2>0，当时，

令则

1当0<m<2即c>时，当r=m时，y′=0；当r∈(0，m)时，则y′<0;当r∈(m，2)时，y′>0，

∴r=m是函数y的极小值点，也是最小值点.

2当m≥2即时，当r∈(0，2)时，y′<0，函数单调递减.

∴r=2是函数y的最小值点.

综上所述，当时，建造费用最小时r=2;当时，建造费用最小时

解法二当且仅当即时等式成立.当即时，当即时，时，y′<0，函数单调递减，∴r=2是函数的最小值点.综上所述，当时，建造费用最小时r=2;当时，建造费用最小时

二、发散训练

已知函数f(x)=x3+3|x-a|(a∈R)，若f(x)在[-1，1]上的最大值和最小值分别记为M(a)，m(a)，求M(a)-m(a).