指数对数函数综合题攻略

以指数、对数函数为背景的函数综合题具体地讲有两大类：一是与指数函数有关的复合函数问题；二是与对数函数有关的复合函数问题，当然也包括指数函数与对数函数知识的交汇与综合.

(1)解决指数函数与对数函数的综合问题时，要注意运用指数、对数函数的图像与性质等知识和研究函数的性质的思想方法来分析解决问题，指数函数和对数函数的图像与性质都受底数a的影响，解决与函数单调性相关问题首先要看底数的范围.

(2)涉及复合函数单调性问题，首先应弄清函数是由哪些基本函数复合得到的，求出复合函数的定义域，然后分层逐一求解内层函数的单调区间和外层函数的单调区间，利用定义证明时可分层比较，对于内外层函数，注意“同增异减”.

(3)指数函数、对数函数与二次函数相结合的复合函数的性质考查是重要题型，注意复合函数单调性的判断方法，尤其注意对数函数中真数大于0的条件.

(4)与指数函数、对数函数有关的复合函数的最值，若复合函数又是二次函数型，往往可以转化为二次函数的最值并结合指、对数函数性质加以讨论.

(5)解决与指数函数、对数函数有关的问题，要注意数形结合思想的运用.

(6)在给定条件下，求复合函数字母的取值范围是常见题型，要重视不等式的知识及函数单调性在这类问题中的应用.

一、例题精讲

例1　已知函数函数g(x)的图像与函数f(x)的图像关于直线y=x对称.

(1)求g(x)的解析式；

(2)讨论g(x)在(1，+∞)内的单调性，并加以证明；

(3)令h(x)=1+logax，当[m，n]⊆(1，+∞)(m<n)时，g(x)在[m，n]上的值域是[h(n)，h(m)]，求a的取值范围.

解题策略　这是一道与对数函数有关的综合题，考查反函数的概念、复合函数单调性的证明，以及定义域与值域的对应关系的研究.第(1)问，提供了求已知函数图像关于某一直线(或点)对称的图像所对应函数的解析式的一般方法，即在欲求解析式的图像上任取一点(x，y)，求出它关于已知直线(或点)对称的点的坐标(x′，y′)，根据(x′，y′)所在的图像对应的解析式，代入找到x与y的关系式，即求得欲求的函数解析式；第(2)问，复合函数单调性的证明，一定要注意其规则是同增异减；第(3)问，定义域与值域的对应关系问题可转化为方程根的分布问题，含有参数时，应注意分类讨论，并重视单调性在解题过程中的关键作用.

解：(1)设点P(x，y)是函数g(x)的图像上任意一点，它关于直线y=x对称的点为P′(y，x).依题意P′(y，x)应在函数f(x)的图像上，即于是此即为函数g(x)的解析式.

或x<-1).

(2)设

∴当0<a<1时，g(x1)>g(x2)，∴g(x)在(1，+∞)内是减函数；

当a>1时，g(x1)<g(x2)，∴g(x)在(1，+∞)内是增函数.

(3)当0<a<1时，∵g(x)在(1，+∞)内是减函数，

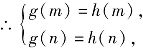即得

即ax2+(a-1)x+1=0，

可知方程的两个根均大于1，即

当a>1时，∵g(x)在(1，+∞)内是增函数，

(舍去).(www.xing528.com)

综上得,

例2　已知函数f(x)=loga(ax-1)(a>0且a≠1).

(1)证明：函数f(x)的图像在y轴的一侧；

(2)设A(x1，y1)，B(x2，y2)(x1<x2)是f(x)的图像上两点，证明：直线AB的斜率大于0；

(3)求函数y=f(2x)与y=f-1(x)的图像的交点坐标.

解题策略　第(1)问，探究函数图像的位置必须对a>1，0<a<1两种情形求出函数的定义域，定义域的范围确定了，图像的位置也就确定了；第(2)问，证明kAB>0也必须对a>1，0<a<1两种情况逐一论证，即证在这里，函数的单调性在其中必起“杠杆”作用；第(3)问，求方程组的解即求两函数图像的交点坐标，实质上是解一个指、对数方程组.

解：(1)证明　依题意ax-1>0，即ax>1，当a>1时，f(x)的定义域为(0，+∞)，图像在y轴的右侧；当0<a<1时，f(x)的定义域为(-∞，0)，图像在y轴左侧；

(2)证明　当a>1时，x>0，由0<x1<x2得1<ax1<ax2，x2-x1>0，

∴0<ax1-1<ax2-1，即直线AB的斜率

当0<a<1时，x<0，由x1<x2<0，得ax1>ax2>1，x2-x1>0.

∴直线AB的斜率

(3)由f(x)=loga(ax-1)得f-1(x)=loga(ax+1).

由(1)知f(x)=loga(ax-1)的值域为R，

∴f-1(x)=loga(ax+1)的定义域为R.

由f(2x)=f-1(x)得loga(a2x-1)=loga(ax+1).　①

∴a2x-ax-2=0，∴ax=2或ax=-1(舍去).

∴x=loga2，验证知x=loga2是方程①的解.

∵f-1(x)=loga(ax+1)，∴f-1(loga2)=loga3.∴交点坐标为(loga2，loga3).

二、发散训练

已知函数f(x)=log4(4x+1)-(k-1)x(x∈R)为偶函数.

(1)求常数k的值；

(2)当x取何值时，函数f(x)的值最小？并求出f(x)的最小值；

(3)设试根据实数a的取值，讨论函数f(x)与g(x)的图像的公共点个数.