求函数的值域或最值这类数学问题的技巧性较强,且常常可以一题多解,正如数学教育家G·波利亚所言:“智者通权达变”.常用的方法主要有以下几种.
(1)配方法:适用于二次函数或可化为二次函数型的函数,要特别注意自变量的范围.
(2)判别式法:适用于可化为关于x的二次方程的函数y=f(x),由Δ≥0,求出y的取值范围,要检验函数的这个最值在定义域内是否有相应的x值.
(3)基本不等式法:利用基本不等式求函数值域或极值时,一定要注意满足“一正二定三相等”的原则.
(4)换元法:根据函数解析式的特点常用三角换元、整体代换、和差代换等,用换元法求值域或最值时要注意新变量的取值范围.
(5)数形结合法:从理解函数的几何意义着手,看能否与距离、斜率等相通.
(6)函数单调性法:利用函数在相应区间上的单调性,由于值域或最值是对函数的总体而言,若需对问题分段讨论,最后必须加以整合.
(7)导数法:设y=f(x)的导数为f′(x),由f′(x)=0可求得极值点坐标,若函数定义域为[a,b],则最值必定为极值点和区间端点中函数值的最大值和最小值.
在实际数学问题中,求函数的最值或值域,提问的角度不同,解答方式也会有所差异,求函数最值时还要注意函数的定义域,若定义域为开区间,则在区间端点不可能出现最值.
函数的值域、极值、最值问题在压轴题中常常是其中的一道小题,解好这道小题常常关系到这道大题的全局.
一、例题精讲
例1 (1)求下列函数的值域:
![]()
(2)设函数![]() 的定义域是[n,n+1](n∈N),问f(x)的值域中有多少个整数?
的定义域是[n,n+1](n∈N),问f(x)的值域中有多少个整数?
(3)已知函数![]() 的值域是
的值域是![]() 求m的范围;
求m的范围;
(4)已知函数![]() 的定义域为R,值域为[0,2],求m、n的值.
的定义域为R,值域为[0,2],求m、n的值.
解题策略 第(1)问,1 可运用换元法或单调性法,前法要注意新元的取值范围,后法要抓住定义域;2 可运用函数的有界性法或数形结合法.第(2)问,考查函数在定义域上的单调性.第(3)问,通过求函数的最值确定参数的范围.第(4)问,函数转化为方程,运用方程有实根,判别式大于等于零,再结合韦达定理求得参数的值.
解:(1)1解法一 (换元法) 设![]() 则
则![]()
于是![]()
显然函数g(t)在[0,+∞)上是单调递减函数,![]()
因此原函数的值域是![]()
解法二 (单调性法) 函数的定义域是![]() 当自变量x增大时,2x-1增大,
当自变量x增大时,2x-1增大,![]() 减小.
减小.![]() 增大,因此函数
增大,因此函数![]() 在其定义域上是一个单调递增函数,∴当
在其定义域上是一个单调递增函数,∴当![]() 时,函数取得最大值
时,函数取得最大值![]() 故原函数的值域是
故原函数的值域是![]()
2解法一 (函数的有界性法) 原函数可化为sinx-ycosx=2y,
![]()
令![]() 且
且![]() 则
则![]() 易知x∈R.
易知x∈R.
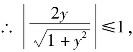 平方得
平方得![]() 即函数的值域为
即函数的值域为![]()
解法二 (数形结合法)![]()
令![]() 易知u2+v2=1.
易知u2+v2=1.
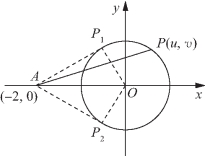
图3-1
∴![]() 可看作圆u2+v2=1上任意一点P(u,v)与点A(-2,0)连线的斜率,如图3-1所示.可得kAP2≤kAP≤kAP1,即
可看作圆u2+v2=1上任意一点P(u,v)与点A(-2,0)连线的斜率,如图3-1所示.可得kAP2≤kAP≤kAP1,即![]()
(2)![]() 的图像是以
的图像是以![]() 为顶点,开口向上的抛物线,而自然数
为顶点,开口向上的抛物线,而自然数![]() 的值域是[f(n),f(n+1)],即
的值域是[f(n),f(n+1)],即![]()
其中最小的整数是n2+n+1,最大的整数是n2+3n+2,
共有(n2+3n+2)-(n2+n+1)+1=2n+2个整数.
(3)由题设知,当x∈[m,1]时,g(x)=x2+x+1的值域是![]()
![]()
(4)令![]() 则(u-m)x2-8x+(u-n)=0.
则(u-m)x2-8x+(u-n)=0.
∵x∈R,且设u-m≠0,∴Δ=(-8)2-4(u-m)(u-n)≥0,
即u2-(m+n)u+(mn-16)≤0.
由1≤u≤9知,关于u的一元二次方程u2-(m+n)u+(mn-16)=0的两根为1和9,由韦达定理,得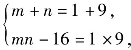 解得m=n=5.
解得m=n=5.
若u-m=0,即u=m时,对应f(x)=log3m的值域不为[0,2],不符合条件,∴m=n=5为所求.
例2 (1)已知y2=4a(x-a)(a>0),且当x≥a时,S=(x-3)2+y2的最小值为4,求参数a的值;
(2)函数![]() 的最大值是________.
的最大值是________.
解题策略 第(1)问,把条件代入二元函数,消元后得到S关于x的一元函数,a为参数,可以发现抛物线的对称轴和区间都在变动,而开口方向是确定的,所以必须讨论对称轴与区间的相对位置得到最小值,根据最小值为a得到关于a的方程,解方程得到参数a的值;第(2)问通过发散思维可以有多种解法.
解:(1)将y2=4a(x-a)(a>0)代入S的表达式,得S=(x-3)2+4a(x-a).(https://www.xing528.com)
则S=[x-(3-2a)]2+12a-8a2,S是x的二次函数,其定义域是x∈[a,+∞),对称轴是x=3-2a,顶点坐标是(3-2a,12a-8a2),图像开口向上.
若3-2a≥a,即0<a≤1时,当x=3-2a时,S的最小值为12a-8a2=4,得![]()
若3-2a<a,即a>1时,当x=a时,S的最小值为[a-(3-2a)]2+12a-8a2=4,此时a=5.
综上讨论,参数a的值是a=1或![]() 或a=5.
或a=5.
(2)解法一 (导数法)![]()
![]()
令y′=0,得![]() 记
记![]()
![]()
解法二 (三角换元法)![]()
∴0≤x-1≤3,则![]() 记
记![]()
![]()
其中![]() 当
当![]() 时,y有最大值
时,y有最大值![]()
解法三 (构造几何图形)![]()
设![]()
故![]()
∴目标直线![]() 与圆u2+v2=3在第一象限的图形相切时取得最大值,由
与圆u2+v2=3在第一象限的图形相切时取得最大值,由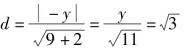 得
得![]() 即为所求的最大值.
即为所求的最大值.
解法四 (构造平面向量)![]()
∴构造平面向量![]()
则![]()
![]() 当且仅当
当且仅当![]() 与
与![]() 同向时取等号.
同向时取等号.
![]()
当且仅当![]() 即
即![]() 时,等号成立.
时,等号成立.![]()
解法五 (构造对偶式,运用单调性)![]()
记![]()
∵u在[1,4]上单调递减,则![]() 故0≤u2≤27.
故0≤u2≤27.
又![]()
故y2=33-u2,∵6≤33-u2≤33,故![]()
故y有最大值![]()
解法六 (柯西不等式)![]() 由柯西不等式有
由柯西不等式有![]()
当且仅当![]() 即
即![]() 时,等号成立,
时,等号成立,![]()
例3 求![]() 的最值,并求出相应的x值.
的最值,并求出相应的x值.
解题策略 解题应崇尚常规思路,切忌“炫技”.本例首先要化简,化简后可能会出现sinx+cosx的形式,通常采用“换元法”转化为代数函数在新元的取值范围内求最值,如果所得函数解析式可以运用均值不等式求最值,则必须符合“一正二定三相等”原则,并落实分类与整合的思想方法.
解:(换元且利用均值不等式)
y![]()
![]() ①
①
设![]()
代入①式,当t=0时,![]() 当t≠0时,
当t≠0时,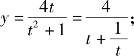
当![]() 时,
时,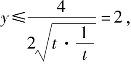 即t=1,也即
即t=1,也即![]() 或
或![]() 时,ymax=2;
时,ymax=2;
当![]() 时,
时, 即t=-1,也即
即t=-1,也即![]()
x=2kπ+π或![]() 时,ymin=-2.
时,ymin=-2.
二、发散训练
已知函数![]() 设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,满足f′(2-x)=f′(x).
设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,满足f′(2-x)=f′(x).
(1)设![]() 求函数g(x)在[0,m]上的最大值;
求函数g(x)在[0,m]上的最大值;
(2)设h(x)=lnf′(x),若对一切x∈[0,1],不等式h(x+1-t)<h(2x+2)恒成立,求实数t的取值范围.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




