高中数学导数型考题盘点

函数既是高中数学中重要的基础知识又是高中数学的主干知识，在高考中占有举足轻重的地位，而导数是解决实际问题强有力的数学工具，运用导数的有关知识，研究函数的性质：单调性、极值和最值、零点是高考考查的热点，且以解答题的形式出现，常常处于压轴的地位.

纵观近年来高考数学压轴题，常出现的题型有两大类型：①构建函数模型求参数的取值范围以及求最值问题，特别是函数与不等式、方程、数列等的综合题，突出渗透数学思想和方法；②以导数为工具考查导数的几何意义，求解或证明数列不等式，研究函数性态及图像，特别是三次函数的图像、性质及其应用、指数或对数与一次或二次函数联袂型性态的研究.

一、例题精讲

例1　(2017年高考数学江苏卷理科第20题)已知函数f(x)=x3+ax2+bx+1(a>0，b∈R)有极值，且导函数f′(x)的极值点是f(x)的零点(极值点是指函数取极值时对应的自变量的值).

(1)求b关于a的函数关系式，并写出定义域；

(2)证明：b2>3a；

(3)若f(x)，f′(x)这两个函数的所有极值之和不小于求a的取值范围.

解题策略　本题主要考查利用导数研究初等函数的单调性、极值及零点问题，考查综合运用数学思想方法分析与解决问题以及逻辑推理能力，其中后两问各有多种证法或解法.第(2)问，可以用导数探究函数的单调性来证明，可以运用均值不等式证明，也可以转化为二次函数通过探究其性质来证明；第(3)问，可以通过导数探求a的取值范围，也可以结合f(x)图像的对称性获得较为简捷的解法，前一种解法需要用到韦达定理，运算量大，后一种解法抓住几何特征运算量相应减少.

解：(1)由f(x)=x3+ax2+bx+1，得

当时，f′(x)有极小值

∵f′(x)的极值点是f(x)的零点，

又∵a>0，故

∵f(x)有极值，故f′(x)=0有实根，从而即a≥3，

当a=3时，f′(x)>0(x≠-1)，故f(x)在R上是增函数，f(x)没有极值；

当a>3时，f′(x)=0有两个相异的实根，列表如下：

故f(x)的极值点是x1、x2，从而a>3，因此定义域为(3，+∞).

(2)证法一　(导数法)　由(1)知

设则

当时，g′(t)>0，从而g(t)在区间内单调递增.

故即因此b2>3a.

证法二　(均值不等式法)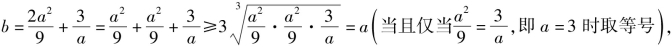而a>3，故等号不成立.

∴b2>a2=a·a>3a.

证法三　(转化为二次函数问题)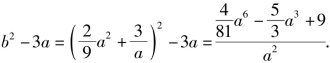

考虑二次函数其中t=a3>27)，

其对称轴故f(t)在区间(27，+∞)内单调递增，

∴[f(t)]min>f(27)=0，故b2>3a.

(3)解法一　(常规解法)　由(1)知，f(x)的极值点是x1、x2，且

从而f(x1)+f(x2)

=

记f(x)，f′(x)所有极值之和为h(a).

∵f′(x)的极值为

于是h(a)在(3，+∞)上单调递减.

于是h(a)≥h(6)，故a≤6，因此a的取值范围为(3，6].

解法二　(妙思巧解)　设f(x)的极值点为x1、x2，则

又f(x)对称中心为(www.xing528.com)

由(1)知从而于是f(x1)+f(x2)=0.

由f′(x)的极小值为则f(x)，f′(x)这两个函数的所有极值之和为易知h(a)是(3，+∞)内的减函数.

由得h(a)≥h(6)，则a≤6，故a的取值范围为(3，6].

例2　(2018年高考数学天津卷理科第20题)

已知函数f(x)=ax，g(x)=logax，其中a>1.

(1)求函数h(x)=f(x)-xlna的单调区间；

(2)若曲线y=f(x)在点(x1，f(x1))处的切线与曲线y=g(x)在点(x2，g(x2))处的切线平行，证明：

(3)证明：当时，存在直线l，使l是曲线y=f(x)的切线，也是曲线y=g(x)的切线.

解题策略　本例是指数与对数函数的联袂型，是高考中函数与导数的热点考题，此类压轴题贯穿始终的是数学思想方法，在含有参数的试题中，通常考查分类与整合思想、函数与方程思想、数形结合思想、化归与转化思想，把不等式问题转化为函数最值问题，把方程的根转化为函数零点问题.第(1)问，先求出h′(x)，然后令h′(x)=0，即可得h(x)的单调区间；第(2)问，利用两函数在两点处的切线平行建立等式，然后进行化简；第(3)问，先分别求出f(x)在点(x1，f(x1))处的切线方程和g(x)在点(x2，g(x2))处的切线方程，然后利用切线重合建立等式，消元后转化为方程的解的问题，在解答过程中要充分注意数学思想方法的应用.

解：(1)由已知，h(x)=ax-xlna，有h′(x)=axlna-lna，令h′(x)=0，解得x=0，由a>1，可知当x变化时，h′(x)，h(x)的变化情况如下表：

∴函数h(x)的单调递减区间为(-∞，0)，单调递增区间为(0，+∞).

(2)证明　由f′(x)=axlna，可得曲线y=f(x)在点(x1，f(x1))处的切线斜率为ax1lna，由可得曲线y=g(x)在点(x2，g(x2))处的切线斜率为这两条切线平行，故有即x2ax1(lna)2=1，两边取以a为底的对数，得

(3)证明　曲线y=f(x)在点(x1，ax1)处的切线l1：y-ax1=ax1lna(x-x1)，曲线y=g(x)在点(x2，logax2)处的切线

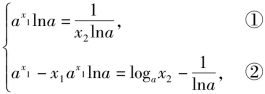要证明当时，存在直线l，使l是曲线y=f(x)的切线，也是曲线y=g(x)的切线，只需证明当时，存在x1∈(-∞，+∞)，x2∈(0，+∞)，使得l1与l2重合，即只需证明当时，方程组有解.

由①得代入②，得③

因此，只需证明当时，关于x1的方程③存在实数解.

设函数即要证明当时，函数y=u(x)存在零点.

u′(x)=1-(lna)2xax，可知x∈(-∞，0)时，u′(x)>0；x∈(0，+∞)时，u′(x)单调递减，又

故存在唯一的x0，且x0>0，使得u′(x0)=0，即1-(lna)2x0ax0=0.

由此可得，u(x)在(-∞，x0)上单调递增，在(x0，+∞)上单调递减，u(x)在x=x0处取得极大值u(x0).

故lnlna≥-1.

∴u(x0)

下面证明存在实数t，使得u(t)<0.

由(1)可得ax≥1+xlna，当时，有

u(x)≤(1+xlna)

∴存在实数t，使得u(t)<0.

因此，当时，存在x1∈(-∞，+∞)，使得u(x1)=0.

∴当时，存在直线l，使l是曲线y=f(x)的切线，也是曲线y=g(x)的切线.

二、发散训练

已知函数f(x)=ex，x∈R.

(1)若直线y=kx+1与f(x)的反函数的图像相切，求实数k的值；

(2)设x>0，讨论曲线y=f(x)与曲线y=mx2(m>0)公共点的个数；

(3)设a<b，比较与的大小，并说明理由.