高中数学微专题——归纳法及分类，含压轴题攻略

归纳法是指通过对特殊的、具体的事物的分析、认识、研究，从而导出一般性结论的方向，它是一种由个别到一般、从特殊到普遍、从经验事实到事物内在规律性的认识手段和模式.

归纳法分类：

归纳法

1.不完全归纳法

不完全归纳法是指通过对某类事物中的一部分对象或一部分子类的考察而概括出该类事物的一般性结论的方法，前提和结论之间未必有必然的联系，由不完全归纳法得出的结论只有或然的性质，结论不一定正确，还需要经过严格的逻辑论证和实践的检验.

2.完全归纳法

完全归纳法是指通过对某类事物中的每一个对象或每一个子类的情况的研究而概括出关于事物的一般性结论的方法，正确的前提必然能得出正确的结论，所以完全归纳法可以作为数学中严格证明的工具，在数学解题中有广泛的应用.完全归纳法包括枚举归纳法和数学归纳法等.

(1)枚举归纳法：将所涉及的研究对象一一列举出来进行研究的方法.这种方法主要适用于研究对象的范畴较小的情况，如整数问题中只需按奇偶数两种情况研究，三角形问题中对形状只需分锐角、直角、钝角3种情况讨论.

(2)数学归纳法：一种证明与正整数n有关的数学命题的重要方法.华罗庚先生说：“把数学归纳法学好了，对进一步学好高等数学有帮助，甚至对认识数学的性质，也会有所裨益.”数学归纳法可以用“多米诺骨牌现象”进行形象地说明：推倒头一块“骨牌”，它会带倒第二块，再带倒第三块……直到所有“骨牌”全部倒下，把骨牌想象为一系列无穷多个编了号的命题：P1，P2，P3，…，假定能够证明：

(奠基)最初的一个命题正确；

(过渡)由每一个命题的正确性可以推出它的下一个命题的正确性，那么我们便证明了这一列命题的正确性.事实上，我们已会“推倒头一块骨牌”，即证明最初的一个命题成立(所谓“奠基”)，而“过渡”则意味着“每一块骨牌在倒下时都将带倒下一块骨牌”，这样一来，并不需要特别强调应推倒哪一块骨牌，事实上，只要头一块一旦倒下，那么这一列中的任何一块骨牌都或迟或早必然倒下.

因此可得数学归纳法的基本形式：

第一数学归纳法：设P(n)是一个关于正整数n的命题，如果(i)P(1)成立；(ii)假设P(k)成立，则P(k+1)也成立，那么，P(n)对任意正整数n都成立.

第二数学归纳法：设P(n)是一个关于正整数n的命题，如果(i)P(1)成立；(ii)假设P(n)对所有适合n<k的正整数成立，则P(k)成立，那么，P(n)对任意正整数n都成立.

归纳法帮你猜想解题思路，归纳与猜想对数学解题是一件锐利的武器，但也是一件危险的武器，所作的猜想仅仅对有限种情况进行了验证，根据有限种情况作出的猜想未必都正确，所以需要用数学归纳法证明猜想的正确性，于是有了“归纳—猜想—证明”类题型.正如G·波利亚所说：“先猜，后证——这是大多数的发现之道.”同样，数学问题也需要猜想，甚至是“大胆猜想”，尽管由归纳推理所得的猜想未必可靠，还需进一步检验，但它由特殊到一般，由具体到抽象的认识功能，对于科学的发现都是十分有用的，观察、实验，对有限的资料作归纳整理，提出猜想，乃是科学研究的最基本的方法之一.猜想应尽量猜之有据，归纳则是形成猜想的有效途径之一.正如G·波利亚指出的：“数学归纳法是一种论证方法，通常用来证明数学上的猜想，而这种猜想是我们用某种归纳方法所获得的.”

一、例题精讲

例1　若数列{an}的通项公式为an=2n-1，bn=2(log2an+1)(n∈N*).

证明：对任意的n∈N*，不等式成立.

解题策略　运用数学归纳法证明与自然数有关的不等式，关键是由n=k时不等式成立推证出n=k+1时不等式成立，此步的证明要具有目标意识，要注意与最终达到的解题目标进行比较，实现恰当的放缩.

证明　由于an=2n-1，故bn=2n(n∈N*)，所证不等式为

1当n=1时，左式右式左式>右式，结论成立.

2假设当n=k(k∈N*且k≥1)时结论成立，即则当n=k+1时，

要证n=k+1时结论成立，只需证即证

由基本不等式知成立，

故成立，所以当n=k+1时，结论成立.

由 12 可知，对任意的n∈N*时，不等式成立.

例2　已知函数f(x)与函数的图像关于直线y=x对称.

(1)在数列{an}中，a1=1，当n≥2时，an>a1，在数列{bn}中，b1=2，Sn=b1+b2+…+bn，若点在函数f(x)的图像上，求a的值；

(2)在(1)的条件下，过点Pn作倾斜角为的直线ln，若ln在y轴上的截距为(bn+1)，求数列{an}的通项公式.

解题策略　本例是一道以数列为载体的能力题，结合函数与解析几何的一些知识，其解题核心是“观察、猜测、抽象、概括、证明”，这是发现问题和解决问题的重要途径.实际上，攻克数学中的难点一般都是在观察归纳、猜想证明的过程中得以突破的.

解：(1)∵函数f(x)是的反函数，

∵点在函数f(x)的图像上，　①

令n=1，得则a=1.

(2)由(1)得a=1，①式可化为　②

直线ln的方程为：

∵ln在y轴上的截距为

结合②式可得　③

由②式可知，当自然数n≥2时，

两式作差得结合③式得

　④

在④式中，令n=2，结合a1=1，可解得a2=1或2，又因为当n≥2时，an>a1，所以a2=2.

同理，在④式中，依次令n=3，n=4，可解得a3=3，a4=4.

由此猜想an=n，然后用数学归纳法证明如下：

(i)当n=1，2，3时，已证成立；

(ii)假设当n=k时命题成立，即ak=k(k∈N*，且k≥3)，

当n=k+1时，由④式可得

把ak=k代入，解得或ak+1=k+1.

由于k≥3，则所以不符合题意，应舍去，故只有ak+1=k+1，则当n=k+1时命题也成立.

综上可知，数列{an}的通项公式为an=n.

例3　函数f(x)=x2-2x-3，定义数列{xn}如下：x1=2，xn+1是过两点P(4，5)，Qn(xn，f(xn))的直线PQn与x轴交点的横坐标.试证明：2≤xn<xn+1<3.

解题策略　本例是与递推数列有关的不等式证明问题，又涉及函数和过定点P(4，5)的直线系方程，常用数学归纳法求解，证明由n=k变化到n=k+1的情况时，要注意不等式证明中常用的放缩法以及数列递推关系和比差法的应用.

证明1当n=1时，x1=2，直线PQ1的方程为令y=0，得

2假设当n=k时结论成立，即2≤xk<xk+1<3，

直线PQk+1的方程为

令y=0，解得

由归纳假设知

即xk+1<xk+2.

∴2≤xk+1<xk+2<3，即当n=k+1时结论成立.

由 12 知对任意的正整数n，2≤xn<xn+1<3.

例4　对于锐角θ，定义数列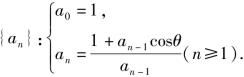

求证：对一切正整数n，均有an>1.

解题策略　在本题的证明过程中，证明n=k+1时直接使用归纳假设ak>1有困难，可以采用以下两种处理方法.

(1)加强命题法，即证明一个更强的命题来达到证明本题的目的，这种证题策略在压轴题中时有出现.

(2)运用跳跃数学归纳法证.证明过程介绍如下：

1当n=1，2，3，…，l时P(1)，P(2)，P(3)，…，P(l)成立；

2假设n=k时，P(k)成立，由此推得n=k+l时，P(n)也成立，那么，根据 12，对于一切正整数n≥1时，P(n)成立.(www.xing528.com)

证法一　(加强命题法)

若对一切正数n，均有an>1，则得

故先证明一个更强的命题：(即“异侧加强”).

1n=1时，即n=1时，命题成立.

2假设n=k时，命题成立，即即

所以即当n=k+1时，命题成立.

综合 12 可知不等式成立.

证法二　(跳跃式数学归纳法)

1n=1时，a1=1+cosθ>1；

n=2时，命题成立.

2假设n=k时，命题成立，即ak>1，

则ak+2

命题对n=k+2成立.

综合 12 可知不等式成立.

例5　证明：对于一切自然数n≥1都有2n+2>n2.

解题策略　本题是关于自然数n的证明题，可利用数学归纳法来证明，但在利用第一数学归纳法讨论当n=k+1时，需要利用(k-3)(k+1)的非负性来得到结论，故需要k≥3，此时，需要在利用数学归纳法时将起点适当增多.

证明1当n=1时，21+2=4>12=1，成立；

当n=2时，22+2=6>22=4，成立.

当n=3时，23+2=10>32=9，成立.

2假设当n=k(k≥3，k∈N)时不等式成立，即2k+2>k2，2k>k2-2.

当n=k+1时，2k+1+2-(k+1)2=2·2k+2-(k2+2k+1)>2(k2-2)+2-(k2+2k+1)=k2-2k-3=(k-3)(k+1).

因为k≥3，即(k-3)(k+1)≥0，

所以2k+1+2-(k+1)2>0，即当2k+1+2>(k+1)2时仍成立.

由 12 所述，原不等式得证.

例6　设数列{an}的前n项和为Sn，满足Sn=2nan+1-3n2-4n，n∈N*，且S3=15.

(1)求a1，a2，a3的值；

(2)求数列{an}的通项公式.

解题策略　通过赋值法运用解方程组求数列的前三项，猜想出通项公式后用数学归纳法证明.

解：(1)解法一　根据已知，可得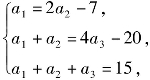解得a1=3，a2=5，a3=7.

解法二　由an+1=Sn+1-Sn知，

Sn=2nan+1-3n2-4n=2n(Sn+1-Sn)-3n2-4n，

可得

又S3=15，可得S2=8，S1=3，所以a1=3，a2=5，a3=7.

(2)解法一　(先猜想，再证明)　由a1=3，a2=5，a3=7，猜测an=2n+1，n∈N*.

下面用数学归纳法证明.

证法一　(第一数学归纳法)

1当n=1，2时，猜想显然成立.

2假设当n=k(k≥1，k∈N*)时ak=2k+1，

根据Sn=2nan+1-3n2-4n，那么，当n≥2时，Sn-1=2(n-1)an-3(n-1)2-4(n-1).

两式作差，并整理得，当n≥2时，

则当n=k+1时，

所以，当n=k+1时，an=2n+1也成立.

综合 12 可知，对任意n∈N*，都有an=2n+1.

证法二　(第二数学归纳法)

1当n=1时，命题显然成立.

2假设当n≤k(k≥1，k∈N*)时，an=2n+1成立.

即a1=3，a2=5，…，ak=2k+1，可得

则当n=k+1时，根据已知Sk=2kak+1-3k2-4k.

可解得ak+1=2k+3=2(k+1)+1，所以，当n=k+1时，an=2n+1也成立.

综合 12 可知，对于任意的n∈N*，都有an=2n+1成立.

解法二　(构造新数列)　当n>1时，由已知得

两式相减得2nan+1=(2n-1)an+6n+1，

即2nan+1-4n2-6n=(2n-1)an-4n2+1，

即2n[an+1-(2n+3)]=(2n-1)[an-(2n+1)].

令bn=an-(2n+1)，则2nbn+1=(2n-1)bn.

由第(1)小题知a1=3，a2=5，则b1=a1-3=0，b2=a2-5=0，即b1=b2=0，

从而bn=0，∴an=2n+1，且n=1时也成立，

故an=2n+1，n∈N*.

二、发散训练

1. 已知函数的最大值不大于又当时，

(1)求a的值；

(2)设证明：

2. 设a0为常数，且an=3n-1-2an-1(n∈Z+).

(1)证明：对任意

(2)假设对任意n≥1，都有an>an-1，求a0的取值范围.