正与逆通常指事物矛盾的双方，反映在数学解题中，主要体现于解题的思维进程中，一般的解决问题的过程，总是先从正面入手进行思考，即从条件出发顺向的思考，这是解题的一种基本的思想方法.大量的习题都是循着正向思维来解决的，强化这种思维定式，在数学解题中有着决定性的作用，但有时会遇到从正面入手不易解决，即正向思维受阻的情况.根据事物往往互为因果，具有双向性和可逆性的特征，此时应从问题的反面去思考，“顺难则逆、直难则曲、正难则反”，顺向推导有困难就逆向推导，直接证明有困难就间接证明，正向求解有困难就反向逆找，探求问题的可能性有困难时就探求不可能性，等式证明从左到右不顺利时就从右到左，即从对立的立场、角度、层次、侧面去进行思考，从而使问题获得解决.“正难则反”的解题方法常能收到意料不到的功效，这种“逆”恰好弥补了“正”的不足.
正难则反的解题方法的运用主要包括两个方面：一是使用定义、定理、公式、法则时的逆向思维；二是运用思想方法时的逆向思维，它包括举反例、反证法、分析法、同一法、主客元的互换、分子有理化、补集思想等方法策略，因为运用逆向思维解题能打破常规，所以解法往往不落俗套.
中国历史上流传至今的“草船借箭”与“司马光砸缸”的故事，其魅力概源于逆向思维.三国时代周瑜妒忌诸葛亮的才能，委托诸葛亮10日之内督造出10万支箭，这根本是办不到的，诸葛亮明知周瑜要害他但还是痛快地答应只需3天便可造出10万支箭，但诸葛亮压根就没有去造，而是“借”，并且不是从朋友，而是从敌人曹操那里去借，并且获得成功，这是诸葛亮处处留心观察天时、地利，精心筹划，随着实际情况而灵活运用的成果，这种开放性思考是周瑜辈所“望尘莫及”的.同样，司马光砸缸救人的故事也体现了逆向思维的功效.因为在一般人的思维中，有人落水，要救人必须让“人离开水”，而仅靠一起玩耍的小伙伴，要做到把人营救出水缸是不可能的，司马光的机智在于面对紧急险情，果断地用石头把缸砸破，让“水离开人”，巧妙地运用“正难则反”的策略解决问题.
在数学学习中应加强逆向思维的训练，注意以下几点.
(1)数学命题中，定理不一定可逆，但定义总是可逆的，应当学会从正反两个方面运用定义，提升数学思维的灵活性的水平.
(2)注意公式的逆用.逆用公式与顺用公式同等重要，有时将公式反用或适当改变公式形式再用，往往能收到化繁为简的效果.
(3)对数学常规问题提法与推断进行逆向思考.
(4)注意解题中的可逆性原则.
正难则反解题策略体现得最完美的是反证法.
证明一个数学命题，当直接证法难以实施时，则可考虑用反证法这一间接证法.但话说回来，何谓反证法？
一般地，在证明一个命题时，从命题结论的反面入手，先假设结论的反面成立，通过一系列正确的逻辑推理，导出与已知条件、已知公理、定理、定义之一相矛盾的结果或者两个相矛盾的结果，肯定了“结论反面成立”的假设是错误的，从而达到了证明结论正面成立的目的，这样一种证明方法就是反证法.
反证法是一种最常见的证明方法，成语“自相矛盾”中“以子之矛攻子之盾”，正是采用了反证法.
反证法一般采用下述3个步骤.
(1)假设：假设所要证明的结论不成立，而设结论的反面成立(一个或几个，视需要而定).
(2)归谬：利用假设及题设条件，运用正确的逻辑推理，导出下面所列5种错误的结论之一：①结论与已知知识相矛盾；②结论与已知条件相矛盾；③结论与(1)步中提出的假设相矛盾；④引出两个互相矛盾的结论；⑤结论就是原结论.
(3)结论：根据排中律，即在同一论证过程中，命题“P”和命题“非P”有一个且仅有一个是正确的，可知原结论成立.
在应用反证法证题时，必须严格按“假设—归谬—结论”的思路进行，3个部分缺一不可，当然，运用反证法的关键在于归谬，因此，反证法又称为归谬法.数学家哈代说过：“反证法是数学家最精良的武器.”数学教育家G·波利亚则说：“归谬法是利用导出一个明显的谬误来证明假设不成立，归谬法是个数学过程，但它和讽刺家所爱好的做法——反话——有几分相似，用反话很明显地采纳某个见解，但强调它并且过分强调它，直到产生一个明显的谬误.”
反证法主要用来解决如下类型的数学问题.
(1)否定性命题：用直接法往往难以下手，而用反证法常常出奇制胜.
(2)唯一性命题：结论以“……唯一”的形式出现，可考虑用反证法证明.
(3)“至多”“至少”类命题：结论以“至多……”或“至少……”形式出现，可考虑用反证法证明.
(4)某些不等式或等式证明：运用反证法书写相对简洁.
(5)命题结论涉及无限集或数目不确定的对象.
(6)命题结论的反面较结论本身具体、简单，直接证明难以下手，而反证法容易上手.
一、例题精讲
例1 已知3个方程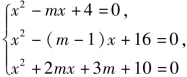
中至少有一个方程有实根，求实数m的取值范围.
解题策略 本题从正面理解“至少”可得3类：①只有一个方程有实根，有3种情况；②只有两个方程有实根，有3种情况；③3个方程都有实根，有一种情况，一一解来整个解题过程显得非常繁杂，若从反面理解，3个方程都没有实根，只有此一种情况，它的反面就是至少有一个方程有实根的种种情况，这就提醒我们可以运用补集的思想方法，即求出3个方程都没有实根时m的取值范围，再求它相对于R的补集，从中可以看出正与逆必是事物矛盾的双方，反映在数学解题中主要体现在解题的思维进程上.通常把综合法的解题方法称为“正”，而把分析法、反证法的解题方法称为“逆”.一般问题的解决过程，总是习惯于先从正面入手，进行思考，这是解题的一种基本的思想方法，但有时会遇到从正面入手不易解决，这时应从问题的反面去思考，这便是“正难则反”，而补集法正是“正难则反”的体现，用这种方法可以收到意料不到的功效，因为这种“逆”恰好弥补了“正”的不足.
解：从反面看，若3个方程都没有实根，则
即m∈(-2，4)时3个方程都没有实根，
再求补集，得3个方程至少有一个方程有实根时，m∈(-∞，-2]∪[4，+∞).
例2 解方程
解题策略 本题若按解3次方程的方法求解，相当困难，如能根据题目特点，让x与
转换一下“角式”，即把常量
看作“未知数”，把x看作常量，则可使本题轻松获解，变换主元，反客为主也应当是“正难则反”解题法的一种.
解：把原方程整理成关于
为“未知数”的“一元二次方程”：(www.xing528.com)
解之得
或
或
例3 (1)设数列{an}是公比为q的等比数列，Sn是它的前n项和，证明：{Sn}不是等比数列.
(2)已知
证明：方程f(x)=0没有负数根.
解题策略 两小题都是否定性命题，此类题从正面突破往往比较困难，用反证法较为合适.
证明 (1)假设{Sn}是等比数列，则
即
∵a1≠0，∴(1+q)2=1+q+q2，即q=0，这与q≠0矛盾，故{Sn}不是等比数列.
(2)假设x0是方程f(x)=0的负数根，则x0<0且
解得
这与x0<0矛盾，故方程f(x)=0没有负数根.
例4 已知数列{an}满足：
数列{bn}满足：
(1)求数列{an}，{bn}的通项公式；
(2)证明：数列{bn}中任意三项不可能成等差数列.
解题策略 第(1)问是由递推关系求通项公式，可通过构造法得特殊数列，再求出其通项公式；第(2)问同上例一样也是否定性命题，即证明数列{bn}中的任意三项不可能成等差数列.若运用综合法证明，这任意三项如何体现？如果能从反面思考，假设数列{bn}存在三项按某顺序成等差数列，则根据等差中项公式立即可得出一个关系式，从这个关系式出发进行变形，看一看是否会得到一个错误的结论，从而得出原命题是正确的结论.
解：(1)由题意可知，
令
则
又
则数列{cn}是首项为
公比为
的等比数列，
即
故
又
故
(2)证明 假设数列{bn}存在三项br，bs，bt(r<s<t)按某顺序成等差数列，由于数列{bn}是首项为
公比为
的等比数列，于是有br>bs>bt，则只可能有2bs=br+bt成立.
两边同乘3t-1·21-r，
化简得3t-r+2t-r=2·2s-r·3t-s. ①
由于r<s<t，∴①式左边为奇数，右边为偶数，故①式不可能成立，导致矛盾，故数列{bn}中任意三项不可能成等差数列.
例5 已知f(x)=ax2+bx+c，若a+c=0，f(x)在[-1，1]上的最大值为2，最小值为
求证：a≠0且
解题策略 证明本题的难点：一是正确写出结论的否定形式；二是当结论的反面不是一种情况时，该如何证明.破解第一个难点，必须熟知命题“p且q”的否定命题“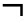
p或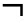
q”，对本题而言，结论“a≠0且
的否定形式是“a=0或
(注意逻辑关系词：“且”“或”)；破解第二个难点，分a=0及
进行讨论，并逐一推出矛盾之处.
证明 (反证法) 假设a=0或
1当a=0时，由a+c=0，得f(x)=bx，显然b≠0，f(x)=bx在[-1，1]上是单调函数，∴f(x)的最大值为|b|，最小值为-|b|.由已知条件得
这与|b|+(-|b|)=0相矛盾，∴a≠0.
2当
时，由二次函数的对称轴为直线
知f(x)在[-1，1]上是单调函数，故其最值在区间的端点处取得.
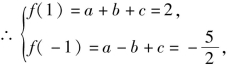或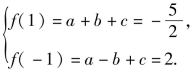
又a+c=0，则此时b无解，
由 12 得a≠0且
二、发散训练
1. 试求常数m的取值范围，使曲线y=x2的所有弦都不能被直线y=m(x-3)垂直平分.
2. 已知x>0，y>0，且x+y>2，求证：
与
中至少有一个小于2.
3. 已知a、b、c∈(0，1)，求证：(1-a)b、(1-b)c、(1-c)a不能同时大于
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
