三角函数与平面向量是高中数学的两块重点内容,两者知识与方法的交汇与综合也是高考重点考查的内容之一.特别是近几年来,已成为高考命题的一个“题眼”,备受命题者的关注,试题常以向量为工具,探讨三角比的求值、化简、证明以及解三角形,探讨三角函数的图像与性质以及与三角函数相关的拓展题、新颖题.
本讲以近几年的高考题为例,对平面向量与三角函数的综合问题进行分类解析,出现较多的有以下三种类型.
(1)题设给出向量的坐标中含有三角函数的形式,运用向量共线或垂直或等式成立等,得到三角函数的关系式,然后求解.
(2)给出用三角函数表示的向量坐标,要求的是向量的模或者其他向量的表达式,解题思路是经过向量的运算,利用三角函数在定义域内的有界性,求得值域等.
(3)运用向量法解三角形主要是向量的垂直与夹角问题,一对向量垂直与向量所在直线的垂直是一致的,向量的线性运算(向量回路)与向量的坐标运算是求解两向量问题的两大途径.关于夹角问题,可以把两个向量的夹角放在三角形中,利用正余弦定理、三角形的面积公式求解;用向量法研究三角形的“四心”(重心、垂心、内心、外心)问题,判断三角形的形状问题也都是常见的题型.
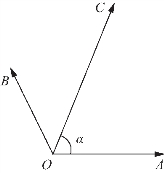
图2-22
一、例题精讲
例1 (2017年高考数学江苏卷第12题)
如图2-22所示,在同一个平面内,向量![]() 的模分别为
的模分别为![]() 与
与![]() 的夹角为α,且
的夹角为α,且![]() 与
与![]() 的夹角为45°,若
的夹角为45°,若![]() 则m+n= .
则m+n= .
解题策略 本题主要考查三角函数的定义、三角恒等变换以及平面向量的数量积运算.平面向量数量积的运算一般有两种解法,一是利用向量数量积的坐标运算求解,二是利用向量数量积的定义和运算性质求解.如果通过添线构造不同的图形可以有多种不同的新颖解法,显得简捷又精彩.
解法一 (通解) 以O为坐标原点,OA所在直线为x轴建立平面直角坐标系,则A(1,0),由![]() 得
得![]()
设C(xC,yC),B(xB,yB),则![]() 即
即![]() 又
又![]() 则
则![]() 即
即![]() 由
由![]() 可得
可得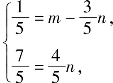 解得
解得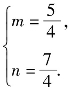
![]()
解法二 (优解一) 由![]() 得
得![]()
则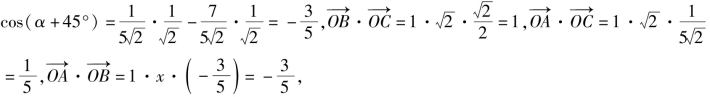
由![]() 得
得![]() 即
即![]() ①
①
同理可得![]() 即
即![]() ②
②
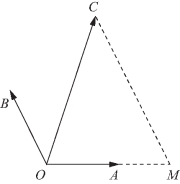
图2-23
联立①②,解得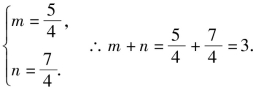
解法三 (优解二) 过点C作OB的平行线交直线OA于点M,如图2-23所示,则![]() 中,由正弦定理得
中,由正弦定理得![]()
即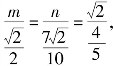 解得
解得![]()
解法四 (优解三) 如图2-24所示,联结AB交OC于点D,
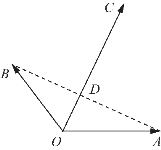
图2-24
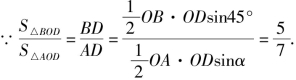
![]()
从而![]()
![]() 于是
于是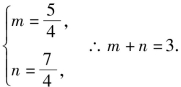
例2 (1)已知7sinα+24cosα=25,求tanα的值;
(2)已知![]() 求锐角α、β;
求锐角α、β;
(3)运用向量法证明:cos(α-β)=cosαcosβ+sinαsinβ.
解题策略 第(1)、(2)两问,作为三角求值或求角,完全可以在三角函数范围内解,但若运用向量法解,则思维简约,过程快捷;第(3)问,两角差的余弦公式有多种证明方法.运用向量法证明可以开阔思路,拓展视野.
解:(1)注意到系数满足72+242=252,可构造向量![]()
于是由![]() 可得
可得![]() 即7=25sinα,24=25cosα,故
即7=25sinα,24=25cosα,故![]()
(2)由已知得![]() ①
①
构造向量![]()
由于![]()
![]()
又由![]() 有
有![]() 即
即![]()
![]() 即
即![]() 将
将![]() 代入①式并整理得
代入①式并整理得
![]()
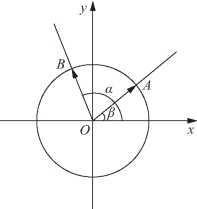
图2-25
(3)证明 在单位圆O上任取两点A、B,以Ox为始边,以OA、OB为终边的角分别为β、α,如图2-25所示.
则A点坐标为(cosβ,sinβ),B点坐标为(cosα,sinα),则向量![]() 它们的夹角为α-β.
它们的夹角为α-β.![]() 由向量夹角公式得:
由向量夹角公式得: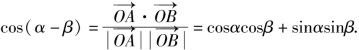 即cos(α-β)=cosαcosβ+sinαsinβ.
即cos(α-β)=cosαcosβ+sinαsinβ.
例3 设![]() 为单位向量,非零向量
为单位向量,非零向量![]() 若
若![]() 的夹角为
的夹角为![]() 则
则![]() 的最大值等于 .
的最大值等于 .
解题策略 本题表述简洁清晰,可从坐标入手,运用配方法求最值;也可从方程角度入手,运用判别式法确定范围而获得最值;若从“形”的角度入手,则更奇妙.
解法一 设![]() 则
则![]()
当x=0时,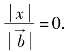
当x≠0时,![]()
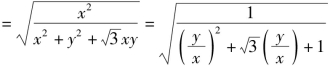
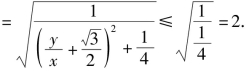
解法二 设 可得
可得![]() 当x≠0时,
当x≠0时,![]()
有![]() 解得t∈[0,2],即
解得t∈[0,2],即![]() 的最大值为2.
的最大值为2.

图2-26
解法三 如图2-26所示,设![]() 则
则![]() 当点E在∠AOB内时,显然有
当点E在∠AOB内时,显然有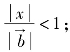 当点E在∠AOB外时,在△ODE中,由正弦定理知
当点E在∠AOB外时,在△ODE中,由正弦定理知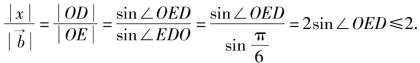 当且仅当
当且仅当![]() 时,等号成立,故
时,等号成立,故![]() 的最大值为2.
的最大值为2.
例4 在平面直角坐标系中,点O(0,0),P(6,8),将向量![]() 绕点O按逆时针方向旋转
绕点O按逆时针方向旋转![]() 后得向量
后得向量![]() 则点Q的坐标是( ).
则点Q的坐标是( ).
![]()
![]()
![]()
解题策略 本题可以利用向量所成角的余弦值与向量的模构造方程,求出点的坐标,也可以将向量的旋转转化为三角函数的运算求解.
解法一 设点Q的坐标为(x,y),由题意知![]()
又![]() ①(https://www.xing528.com)
①(https://www.xing528.com)
∵向量![]() 与
与![]() 的夹角为
的夹角为![]() 且点Q在第三象限,
且点Q在第三象限,
∴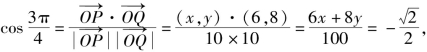
∴6x+8y=![]() ②
②
联立①②,解得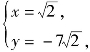 或
或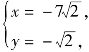
又∵点Q在第三象限,∴点Q的坐标为![]() 选A.
选A.
解法二 设![]() 又
又![]() 设点Q的坐标为(x,y),由题意知
设点Q的坐标为(x,y),由题意知![]() 则点Q的坐标又可表示为
则点Q的坐标又可表示为![]()
![]()
![]()
∴点Q的坐标为![]() 选A.
选A.
例5 在平面直角坐标系xOy中,已知向量![]()
(1)若![]() 求tanx的值;
求tanx的值;
(2)若![]() 与
与![]() 的夹角为
的夹角为![]() 求x的值.
求x的值.
解题策略 本题可借助向量数量积的坐标运算将问题转化为三角函数求值、求角问题,构建方程是解题的关键,应注意两角和与差公式的逆用和角的范围.
解:(1)∵向量![]() 且
且![]()
又![]() 则
则![]() 即
即![]()
![]()
(2)由(1)知,![]()
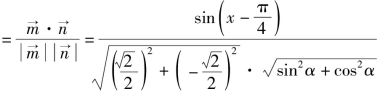
![]()
![]() 又
又![]()
![]() 即
即![]()
例6 已知向量![]()
(1)求向量![]() 的长度的最大值;
的长度的最大值;
(2)设![]() 且
且![]() 求cosβ的值.
求cosβ的值.
解题策略 本题考查对向量的加法,数量积的坐标运算公式的运用以及三角函数知识.在由两个角的三角函数值相等确定角的关系时,要注意三角函数的周期性与奇偶性对结果的影响.
解:(1)解法一![]()
则![]()
=2(1-cosβ).
![]() 即
即![]()
当cosβ=-1时,有![]() 向量
向量![]() 的长度的最大值为2.
的长度的最大值为2.
解法二![]()
当cosβ=-1时,有![]() 即
即![]() 向量
向量![]() 的长度的最大值为2.
的长度的最大值为2.
(2)解法一 由已知可得![]()
![]()
![]() 即cos(α-β)=cosα.
即cos(α-β)=cosα.
由![]() 得
得![]() 即
即![]()
![]() 或β=2kπ(k∈Z).于是cosβ=0或cosβ=1.
或β=2kπ(k∈Z).于是cosβ=0或cosβ=1.
解法二 若![]() 则
则![]() 又由
又由![]() 得
得![]()
![]() 即
即![]()
∴sinβ=1-cosβ平方得sin2β=(1-cosβ)2,1-cos2β=(1-cosβ)2,
(1-cosβ)(1+cosβ-1+cosβ)=0.即cosβ(cosβ-1)=0.
解得cosβ=0或cosβ=1,经检验cosβ=0或cosβ=1即为所求.
例7 已知![]() 为不共线的向量,t∈R.
为不共线的向量,t∈R.
(1)求![]() 的最小值及相应的t值;
的最小值及相应的t值;
(2)求存在两个正数t1,t2且t1≠t2,使![]() 的充要条件.
的充要条件.
解题策略 求向量模的最值问题的关键是利用![]() 将模的问题转化为数量积的问题.
将模的问题转化为数量积的问题.
解:(1)
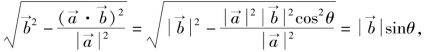 其中θ为向量
其中θ为向量![]() 的夹角,
的夹角,
故当![]() 时,
时,![]() 有最小值
有最小值![]()
(2)由(1)及t>0知,cosθ>0,即![]() 与
与![]() 的夹角为锐角.
的夹角为锐角.
在此前提下,存在t1、t2∈R+,且t1≠t2,使![]() 的充要条件是
的充要条件是![]() 有两正解.
有两正解.
可得![]()
即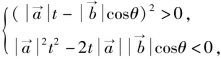 亦即
亦即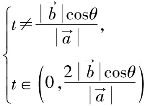
故所求充要条件为![]() 与
与![]() 的夹角为锐角,且
的夹角为锐角,且![]()
二、发散训练
1.(1)求函数y=2cosα-3sinα的最大、最小值及取最值时tanα的值.
(2)在锐角△ABC中,若a=7,b=8,向量![]() 且
且![]() 则△ABC的面积为( ).
则△ABC的面积为( ).
![]()
(3)已知向量![]() 若对任意单位向量
若对任意单位向量![]() 均有
均有![]() 则
则![]() 的最大值是 .
的最大值是 .
2. 已知向量![]()
(1)若![]() 求x的值;
求x的值;
(2)记![]() 求f(x)的最大值和最小值.
求f(x)的最大值和最小值.
3. 已知向量![]() 设函数
设函数![]() 且f(x)的图像过点
且f(x)的图像过点![]() 和点
和点![]()
(1)求m、n的值;
(2)将y=f(x)的图像向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图像,若y=g(x)图像上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调递增区间.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




