在解题过程中,通过引入一个或几个新变量来代替原式中某些量以实现变量替换,从而使问题得以解决.这种解题方法叫作引参换元法,又称辅助元素法,引参换元的理论依据是等量代换.
引参换元的关键是实施未知量或变量的替代,替代关系的确定常有以新元代旧元、以新元替旧式、赋旧元以新式、以新式替旧式这几种.引参换元可以把分散条件联系起来,或者把隐含的条件显示出来,或者把条件与结论联系起来,或者把陌生的形式变换为熟悉的形式,把繁难的计算和推理论证简化,从而达到化难为易、化繁为简、化未知为已知的目的,以利于问题的解决.引参换元时一定要注意新元的约束条件和整体置换策略的运用,适时限定条件以符合原未知数取值范围的要求.
引参换元的基本步骤如下:
(1)把原问题中的某个式子或几个式子分别看成一个整体;
(2)引入新字母或新式代替这些式子,使以新元或新式为基础的问题较为简洁易解;
(3)对以新元或新式为基础的问题进行解答,得出结果;
(4)再代回原来的式子中求出原变量的结果.
引参换元通常有三角换元、线性换元、自身换元、整体换元、增量换元、均值换元、求和换元、常量换元等多种形式,引参换元广泛运用于求解方程、因式分解、求函数的值域或最值、恒等式或不等式的证明、坐标变换、数列等,是数学解题中应用最为广泛的一种方法.正如G·波利亚所说的:“引入辅助元是引人注目的一步,人的高明之处就在于当他碰到一个不能直接克服的障碍时,他会绕过去;当原来的问题看起来似乎不好解时,就会想出一个合适的辅助问题,构想一个辅助问题是一项重要的思维活动.”
G·波利亚还认为,引入辅助元素可“使问题的概念更完整,更富有启发性,更为人所熟悉”,是个“好念头”.因此,当问题的条件和结论不易发生关系或关系不明朗时,借助辅助元素——参数为桥梁或探测器,可使条件和结论联结起来,关系明朗,问题可解,这就是参数思想的基本点.
参数思想解题的特征是:引入参数,参与推导;消去参数,显露结论.
参数思想在解析几何内容中占有很重的分量,直线方程、圆锥曲线方程的一般形式中的字母系数都可看作参数,应用参数方程解题更是解析几何研究中的重头戏,方法灵活、独树一帜.
一、例题精讲
例1 若a、b为正实数,且a+b=1,求证:![]()
解题策略 考虑到条件是a+b=1,可实施均值代换:![]() 代入a4+b4可使式子利用非负值方法求证.
代入a4+b4可使式子利用非负值方法求证.
证明 令![]() 且
且![]() 则
则![]()
例2 设x1、x2是方程x2-6x+1=0的两个根,求证:对一切自然数![]() 都是偶数.
都是偶数.
解题策略 由两根之和之积为定值,可运用和差代换,结合二项式定理证之.
证明 由根与系数关系得:x1+x2=6,x1x2=1.
故令x1=3+t,x2=3-t,由x1x2=1得(3+t)(3-t)=1,∴t2=8.
![]()
![]()
![]()
因此,![]() 都是偶数.
都是偶数.
例3 (1)已知1≤x2+y2≤2,求z=x2-xy+y2的最值;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,设![]() 求sinB的值.
求sinB的值.
解题策略 第(1)问,二元函数转变为一元函数,由条件1≤x2+y2≤2,考虑三角换元能实现降元的目标;第(2)问,通过均值换元可将三元降为二元、二元降为一元.从而达到变繁为简、化难为易、化未知为已知的数学解题策略.
解:(1)令x=kcosθ,y=ksinθ,则1≤k2≤2.
又![]()
∴当k2=2,sin2θ=-1时,zmax=3;当k2=1,sin2θ=1时,![]()
(2)![]() 可设
可设![]() 即
即![]()
∴B=π-(A+C)=π-2θ,sinB=sin2θ.
由a+c=2b,根据正弦定理可得sinA+sinC=2sinB.
![]() 故
故![]()
![]()
则![]()
因此![]()
例4 (1)给定两个长度为1的平面向量![]() 和
和![]() 它们的夹角为120°,点C在以O为圆心的圆弧
它们的夹角为120°,点C在以O为圆心的圆弧![]() 上运动,若
上运动,若![]() 中x、y∈R,则x+y的最大值为 ;x-y的取值范围是 .
中x、y∈R,则x+y的最大值为 ;x-y的取值范围是 .
(2)在扇形OAB中,OA=1,∠AOB=60°,C为弧![]() 上的一个动点,若
上的一个动点,若![]() 则x+3y的取值范围是 .
则x+3y的取值范围是 .
解题策略 本例两小题可以有多种解法,若建立平面直角坐标系,设动点C的坐标为三角形式,则是一种非常巧妙的解法.
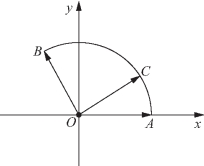
图2-12
解:(1)如图2-12所示,以O为坐标原点,OA所在直线为x轴建立平面直角坐标系.则![]() 设∠AOC=θ,则
设∠AOC=θ,则![]()
由于![]()
根据![]() 得到
得到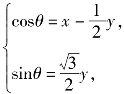 从而
从而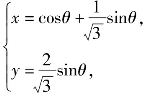
故![]() 当
当![]() 时,(x+y)max=2.
时,(x+y)max=2.
![]() 又
又![]()
![]() 即-1≤x-y≤1.
即-1≤x-y≤1.

图2-13
(2)如图2-13所示,以O为坐标原点,OA所在直线为x轴建立平面直角坐标系,则![]() 设∠AOC=θ,则
设∠AOC=θ,则![]()
由![]() 得
得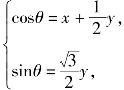 从而
从而
则![]() 易知
易知![]()
故![]() 在
在![]() 上单调递增,而
上单调递增,而![]()
![]()
![]()
故x+3y∈[1,3].
例5 (1)如图2-14所示,已知在矩形ABCD中,点C(4,4),点A在曲线x2+y2=9(x>0,y>0)上移动,且AB、BC两边始终分别平行于x轴、y轴.求使矩形ABCD的面积最小时点A的坐标;
(2)如图2-15所示,已知曲线4x2+9y2=36(x>0,y>0).点A在曲线上移动,点C的坐标为(6,4),以AC为对角线作矩形ABCD,使AB∥x轴,AD∥y轴,求矩形ABCD面积最小时点A的坐标.
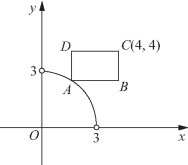
图2-14
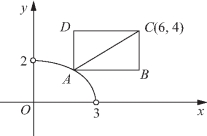
图2-15
解题策略 第(1)问,令![]() 则原问题可转化为三角函数求最小值;第(2)问,令
则原问题可转化为三角函数求最小值;第(2)问,令![]() 此时两小题的解析式都出现了sinθ+cosθ及sinθcosθ的形式,再令sinθ+cosθ=t进行第二次换元,将所求的问题转化为二次函数最值的问题,充分体现了“设参换元”的战术构想,当然“设参换元”后要注意前后新旧变元取值范围的不同.
此时两小题的解析式都出现了sinθ+cosθ及sinθcosθ的形式,再令sinθ+cosθ=t进行第二次换元,将所求的问题转化为二次函数最值的问题,充分体现了“设参换元”的战术构想,当然“设参换元”后要注意前后新旧变元取值范围的不同.
解:(1)设![]()
则SABCD=(4-3cosθ)(4-3sinθ)=16-12(sinθ+cosθ)+9sinθcosθ.
令t=sinθ+cosθ,则![]() 其中
其中![]()
于是,有![]()
当![]() 时,SABCD的最小值为
时,SABCD的最小值为![]() 此时
此时
得点A的坐标为![]() 或
或![]()
(2)设![]()
则SABCD=(6-3cosθ)(4-2sinθ)=24-12(sinθ+cosθ)+6sinθcosθ.
令t=sinθ+cosθ,则![]() 其中
其中![]()
于是,有SABCD=3(t-2)2+9,从而可得,当![]() 时,SABCD有最小值
时,SABCD有最小值![]() 此时点A的坐标为
此时点A的坐标为![]()
例6 (1)函数![]() 的最大值是 ;
的最大值是 ;
(2)将边长1m的正三角形薄铁皮沿一条平行于某边的直线剪成两块,其中一块是梯形,记![]() 则S的最小值是 ;
则S的最小值是 ;
(3)设a、b、c是正实数,且abc+a+c=b,求证:![]()
解题策略 第(1)问,可以借助三角换元发现所给函数的几何意义是定点与动点之间连线的斜率,即可运用直线与半圆的位置关系(相切)求得y的最大值;第(2)问的解法众多,其中通过三角换元利用三角函数的有界性解不等式求最值是一种妙思巧解;第(3)问,由于条件是三元等式,如何实现三角换元需要精心构思,从而说明了数学是灵动的.通过思维完成构想,一旦成功何等快意.正如欧阳修的诗句:“一阕声长听不尽,轻舟短楫去如飞.”
解:(1)![]() 由定义知1-x2≥0且2+x≠0.
由定义知1-x2≥0且2+x≠0.
∴-1≤x≤1,故可设x=cosθ,θ∈[0,π],
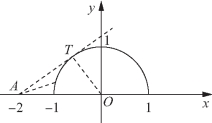
图2-16
则有![]() 可看作是动点M(cosθ,sinθ)(θ∈[0,π])与定点A(-2,0)连线的斜率.动点M的轨迹方程为
可看作是动点M(cosθ,sinθ)(θ∈[0,π])与定点A(-2,0)连线的斜率.动点M的轨迹方程为![]() 即x2+y2=1,y∈[0,1]是半圆(如图2-16所示).
即x2+y2=1,y∈[0,1]是半圆(如图2-16所示).
设切线为AT,T为切点,|OT|=1,|AO|=2,
![]()
因此,函数的值域为![]() 故最大值为
故最大值为![]()
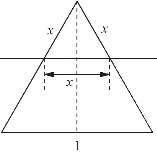
图2-17
(2)如图2-17所示,设梯形上底边长为x,则梯形两腰为1-x,高为![]()
S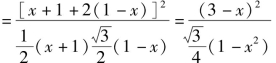
![]()
解法一 令x=sinθ,其中![]() 则
则![]()
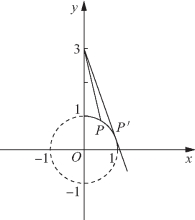
图2-18
设![]() 其几何意义是表示定点A(0,3)和动点
其几何意义是表示定点A(0,3)和动点![]() 两点连线的斜率,且动点P的轨迹是单位圆x2+y2=1上位于第一象限的一段弧,如图2-18所示,设直线AP的方程为y=kx+3.
两点连线的斜率,且动点P的轨迹是单位圆x2+y2=1上位于第一象限的一段弧,如图2-18所示,设直线AP的方程为y=kx+3.
当直线与圆弧相切时(切点P′),由圆心到直线距离等于半径,求得![]() 由数形结合的方法易得
由数形结合的方法易得![]()
由此可知,![]() 即
即![]()
解法二![]()
令x=cosθ,其中![]() 则
则![]()
记![]() 则tsinθ+cosθ=3,即
则tsinθ+cosθ=3,即![]()
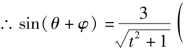 其中角φ满足
其中角φ满足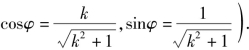
由![]() 得k2≥8,故得
得k2≥8,故得![]()
即![]()
(3)证明 由abc+a+c=b,得![]() 其特征与两角和的正切相似.
其特征与两角和的正切相似.
设![]() 则b=tan(α+β).
则b=tan(α+β).
![]()
![]()
![]()
=2[cos2α+cos2β-cos2(α+β)]
=cos2α+cos2β-2cos2(α+β)+2
=2cos(α+β)cos(α-β)-2cos2(α+β)+2
≤2cos(α+β)-2cos2(α+β)+2
=-2cos2(α+β)+2cos(α+β)+2
![]() 证毕.
证毕.
例7 已知![]() 且x、y为实数,|z1|+|z2|=6.
且x、y为实数,|z1|+|z2|=6.
求f(x,y)=|2x-3y-12|的最大值和最小值.
解题策略 明确复数方程|z1|+|z2|=6对应的轨迹,运用三角换元把二元函数转化为三角函数最值问题.
解:由![]() 令
令![]() (θ为参数).
(θ为参数).
将f(x,y)转化为g(θ)=|6cosθ-6sinθ-12|.
![]()
当![]() 即
即![]() 时,
时,![]()
当![]() 即
即![]() 时,
时,![]()
例8 (1)在双曲线x2-2y2=2上,求一点P,使它到直线x+y=0的距离最短,并求出这个最短距离;
(2)设P为等轴双曲线x2-y2=1上的点,F1、F2为两个焦点,证明:|F1P||F2P|=![]() .
.
解题策略 第(1)问,对所给双曲线进行三角换元,即动点P为三角形式,求点到直线距离所得等式转化为一元二次方程,并用判别式法求d的最小值及相应点P的坐标;第(2)问,利用双曲线的参数方程![]() 并对等式左、右两边所得三角式化简可证.
并对等式左、右两边所得三角式化简可证.
解:(1)设双曲线![]() -y2=1上一点P的坐标为
-y2=1上一点P的坐标为![]() 且
且![]() 则它到直线x+y=0的距离为
则它到直线x+y=0的距离为
 从而
从而![]()
去分母,整理得![]()
∵sinθ是实数,![]() 解之,得
解之,得![]()
当![]() 时,
时,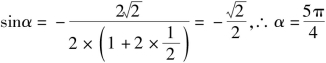 或
或![]() (https://www.xing528.com)
(https://www.xing528.com)
这时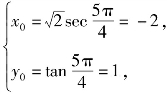 或
或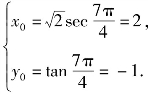
故当双曲线上的点P为(-2,1)或(2,-1)时,它到直线x+y=0的距离最小,这个最小值为![]()
(2)证明 设等轴双曲线x2-y2=1上动点P的坐标为![]() 为参数,0≤θ<2π且
为参数,0≤θ<2π且![]() 焦点
焦点![]()
则![]()
![]()
=4sec4θ-4sec2θ+1=(2sec2θ-1)2,则|F1P||F2P|=2sec2θ-1.
又![]() =sec2θ+tan2θ=2sec2θ-1.
=sec2θ+tan2θ=2sec2θ-1.
由此得|F1P||F2P|=![]() .
.
例9 (1)已知P是椭圆![]() 在第一象限内的点,A(2,0),B(0,1),O为原点,求四边形OAPB的面积的最大值;
在第一象限内的点,A(2,0),B(0,1),O为原点,求四边形OAPB的面积的最大值;
(2)实数x、y满足![]() 若x+y-k>0恒成立,求k的取值范围.
若x+y-k>0恒成立,求k的取值范围.
解题策略 第(1)问,利用椭圆的参数方程,用割补法求四边形OAPB面积,辅助角公式求最值,如果我们以OP分割四边形OAPB,则可得到一种更为简捷的解法.可见,同样用割补法,如何割补大有讲究.第(2)问,用三角换元,将解析几何问题转化为含参三角不等式恒成立问题,再运用“参变分离”转化为三角函数的值域问题,从而求出参数的范围.
解:(1)解法一 设![]()
则![]()
∴所求面积的最大值为![]()
解法二 设![]()
则![]()
∴所求面积的最大值为![]()
(2)由![]() 可设
可设 则
则![]()
代入不等式x+y-k>0,得3cosθ+4sinθ-k>0,
即![]()
而[5sin(θ+φ)]min=-5,∴k<-5.
例10 点P(x,y)在椭圆![]() 上移动时,求函数u=x2+2xy+4y2+x+2y的最大值.
上移动时,求函数u=x2+2xy+4y2+x+2y的最大值.
解题策略 要设法将二元函数的最值问题转化为一元函数的最值问题,注意到椭圆上任一点可设为P(2cosθ,sinθ),这一目标显然容易达到,然而所得三角式的形式仍然比较复杂,需要又一次换元引进新的参变量,如果说“转化”是重要的数学思想,那么换元引参则是实现“转化”的重要途径,在解决数学问题时,要善于运用换元引参达到转化的目的.换元引参解题的特征概括起来是:引入参数,参与推导;消去参数,显露结论.
解:设P(2cosθ,sinθ),θ∈[0,2π),于是
u=x2+2xy+4y2+x+2y=4cos2θ+4sinθcosθ+4sin2θ+2cosθ+2sinθ
=2[(cosθ+sinθ)2+(cosθ+sinθ)+1].
令![]()
于是![]()
当![]() 即
即![]() 时,u有最大值.
时,u有最大值.
![]() 时,
时,![]()
例11 椭圆![]() 上有两点P、Q,O为原点,联结
上有两点P、Q,O为原点,联结![]()
(1)求证:![]() 等于定值;
等于定值;
(2)求线段PQ中点M的轨迹方程.
解题策略 由于P、Q是椭圆上的两个符合特定条件下的动点,于是可设P(4cosθ1,2sinθ1)、Q(4cosθ2,2sinθ2),即通过换元引入双参数θ1、θ2,转化为三角问题求解,双参数虽然看似复杂,但只要在求解过程中合理运用三角恒等变形就可得到定值.而第(2)问在求PQ中点M的参数方程后,再运用“消参法”消去所含参数得所求的轨迹方程.
解:(1)证明 由![]() 设
设![]() (即由“三角换元”引进参数θ).
(即由“三角换元”引进参数θ).
则P(4cosθ1,2sinθ1),Q(4cosθ2,2sinθ2)(P、Q均为动点,故引进双参数θ1、θ2)
则![]() 整理得:cosθ1cosθ2+sinθ1sinθ2=0,即cos(θ1-θ2)=0.
整理得:cosθ1cosθ2+sinθ1sinθ2=0,即cos(θ1-θ2)=0.
∴![]() =16cos2θ1+4sin2θ1+16cos2θ2+4sin2θ2
=16cos2θ1+4sin2θ1+16cos2θ2+4sin2θ2
=8+12(cos2θ1+cos2θ2)=8+6(1+cos2θ1+1+cos2θ2)
=20+6(cos2θ1+cos2θ2)=20+12cos(θ1+θ2)cos(θ1-θ2)=20,
即![]() 等于定值20.
等于定值20.
(2)由中点坐标公式得线段PQ的中点M的坐标为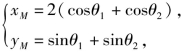 此即为点M的参数方程.
此即为点M的参数方程.
![]()
即所求线段PQ的中点M的轨迹方程为![]()
例12 实数x、y满足4x2-5xy+4y2=5,设S=x2+y2,求![]() 的值.
的值.
解题策略 本例有多种引入参数的方法.方法一:由x2+y2=S,联想到三角公式cos2α+sin2α=1,引进参数α,通过“三角换元法”将问题转化为熟悉的简单三角函数求S的最大值和最小值.还可由![]() 的有界性,即解不等式
的有界性,即解不等式![]() 求S的最大值和最小值.方法二:采用“均值换元法”,将问题转化为二次函数或二次方程,用判别式求解.方法三:引进两个参数m、n,采用“对偶换元法”(和差换元)将问题转化为二次函数求解.
求S的最大值和最小值.方法二:采用“均值换元法”,将问题转化为二次函数或二次方程,用判别式求解.方法三:引进两个参数m、n,采用“对偶换元法”(和差换元)将问题转化为二次函数求解.
解法一 设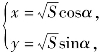 代入条件得4S-5Ssinαcosα=5.
代入条件得4S-5Ssinαcosα=5.
解得![]()
![]()
解法二 由S=x2+y2,设![]()
则![]() 代入已知式得
代入已知式得![]() 移项平方整理得
移项平方整理得
100t2+39S2-160S+100=0,∴39S2-160S+100≤0,解得:![]()
![]()
解法三 设x=a+b,y=a-b,代入条件整理得3a2+13b2=5,则![]()
![]()
![]()
例13 过点A(2,1)作椭圆![]() 的弦PQ,使点A是PQ的三等分点,求PQ所在直线的方程.
的弦PQ,使点A是PQ的三等分点,求PQ所在直线的方程.
解题策略 若设过点A(2,1)的直线方程为y-1=k(x-2),代入椭圆方程求出交点坐标(用k表示),再运用定比分点公式求出k的值,当然可以这样解,但运算量相当大,若运用直线参数方程,利用参数t的几何意义得t2=-2t1,整个解题过程简捷多了.
解:设椭圆中过点A的弦PQ所在直线的倾斜角为α,则PQ的参数方程为![]() (t为参数). ①
(t为参数). ①
将①代入椭圆方程,整理后得(3sin2α+1)t2+4(cosα+2sinα)t-8=0,
∴![]() ②
②
![]() ③
③
∵点A是弦PQ的三等分点,且点A在P、Q之间,∴t2=-2t1.
于是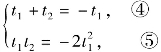
把④代入⑤,得t1t2=-2(t1+t2)2, ⑥
把②③代入⑥,得![]()
化简后得12tan2α+16tanα+3=0,解得![]()

图2-19
∴直线PQ的方程为![]() 或
或![]()
例14 如图2-19所示,已知圆O:x2+y2=64,过圆内一点P(3,4)作两条相互垂直的射线与圆O分别交于点Q,S,以PQ,PS为邻边作矩形PQRS.求矩形顶点R的轨迹.
解题策略 本例若用普通方程直接解,解题过程会比较复杂,若将普通方程转化为参数方程,将原问题转化为三角问题,通过三角变换就能较为顺利求出轨迹方程并判定其表示何种曲线.
解:设圆的参数方程为![]() (θ为参数).
(θ为参数).
设Q(8cosα,8sinα),S(8cosβ,8sinβ),顶点R(x,y).
则![]()
由四边形PQRS为矩形,可知![]()
∴(8cosα-3)(8cosβ-3)+8(sinα-4)(8sinβ-4)=0.
64(sinαsinβ+cosαcosβ)-32(sinα+sinβ)-24(cosα+cosβ)+25=0. ①
又∵PR的中点与QS的中点重合,
∴有![]() ②
②
![]() ③
③
于是有②2+③2,得![]() ④
④
将②③④均代入①,得
![]() 即x2+y2=103.
即x2+y2=103.
又当射线PQ⊥x轴时,![]()
由对称性得![]() 此时|OR|2=103.
此时|OR|2=103.
即对PQ⊥x轴时,同样有|OR|2=103.
综上所述,矩形顶点R的轨迹方程为x2+y2=103,其轨迹即为圆心在原点、半径为![]() 的一个圆.
的一个圆.
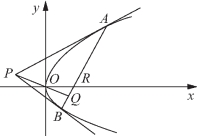
图2-20
例15 (2014年全国高中数学联赛试题)如图2-20所示,在平面直角坐标系xOy中,P是不在x轴上的一个动点,过点P可作抛物线y2=4x的两条切线,两切点A、B的连线与PO垂直,设直线AB与直线PO、x轴的交点分别为Q、R.
(1)证明:R是一个定点;
(2)求![]() 的最小值.
的最小值.
解题策略 本例运用直线参数方程并利用参数的几何意义求解较为方便.过点P的直线PO的参数方程与直线AB的参数方程联立,求得P值即为有向线段PQ的数量.
解:(1)证明 设R(x0,0)(x0>0),直线AB的参数方程为
![]() (t为参数). ①
(t为参数). ①
将①代入y2=4x,得(sin2α)t2-(4cosα)t-4x0=0.
设A(x0+t1cosα,t1sinα),B(x0+t2cosα,t2sinα),
则抛物线y2=4x在点A、B处的切线方程分别为
PA:(t1sinα)y=2(x+x0+t1cosα),
PB:(t2sinα)y=2(x+x0+t2cosα).
联立解得P(-x0,2cotα).
![]()
又PO⊥AB,∴kPO·kAB=-1,即![]() 得x0=2.故R(2,0)为定点.
得x0=2.故R(2,0)为定点.
(2)由(1)知,P(-2,2cotα).设直线PO的参数方程为
![]() (p为参数),即
(p为参数),即![]() (p为参数).
(p为参数).
与①联立解得![]()
在Rt△OQR中,|QR|=|OR||cosα|=2|cosα|.
![]() 当且仅当2|tanα|=|cotα|,
当且仅当2|tanα|=|cotα|,
即![]() 时等号成立,故
时等号成立,故![]() 的最小值为
的最小值为![]()
二、发散训练
1.(1)求函数![]() 的值域;
的值域;
(2)已知函数![]() 且x≠0).若实数a、b使得f(x)=0有实根,则a2+b2的最小值为 .
且x≠0).若实数a、b使得f(x)=0有实根,则a2+b2的最小值为 .
2.(1)求函数![]() 的最大值;
的最大值;
(2)求函数![]() 的最大值和最小值;
的最大值和最小值;
(3)求函数![]() 的值域;
的值域;
(4)求函数![]() 的值域;
的值域;
(5)对于c>0,当非零实数a、b满足4a2-2ab+4b2-c=0且使|2a+b|最大时,求![]() 的最小值.
的最小值.
3.(1)已知a>0,b>0且a+2b=1,求证:![]()
(2)a、b、x、y均为正数,且![]() 求证:
求证:![]()
(3)求证:![]()
4.(1)已知x2-xy+y2=1,求x2-y2的取值范围;
(2)设x,y∈R,且3x2+2y2=6x,求x2+y2的取值范围;
(3)若函数f(x)=(1-x2)(x2+ax+b)的图像关于直线x=-2对称,求f(x)的最大值.
5. 在平面直角坐标系xOy中,F是x轴正半轴上的一个动点,以F为焦点,O为顶点作抛物线C,设P是第一象限内C上的一点,Q是x轴负半轴上的一点,使得PQ为抛物线C的切线,且|PQ|=2,圆C1、C2均与直线OP相切于点P,且均与x轴相切(如图2-21所示),求点F的坐标,使圆C1与C2的面积之和取到最小值.
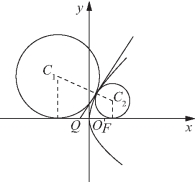
图2-21
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




