放缩法是不等式证明中最重要的变形方法之一.在高考命题的热点——数列不等式的证明——中有广泛的应用,放缩必须有目标,而且要恰到好处,目标往往要从证明的结论考量.
常用的放缩法有增项、减项、利用分式的性质、利用不等式的基本性质,利用已知不等式(如均值不等式、柯西不等式、排序不等式等)、利用函数的性质、利用三角函数的有界性进行放缩等,适当放缩是解决不等式问题的重点也是难点所在.虽然各版教材关于不等式放缩的技巧要求并不高,但高考中和全国数学联赛中经常把对这种方法的考查作为命题的热点,特别是在压轴题中,数列不等式的证明是常考题型.
放缩法主要有直接放缩、裂项放缩、并项放缩、加强放缩等几种类型.
(1)直接放缩:为了证明不等式A<B,可找一个(或多个)中间量C作比较,若能确定A<C与C<B同时成立,则A<B显然正确(实质就是运用不等式基本性质中的传递性).所谓“放”即把A放大到C,再把C放大到B;反之,由B缩小经过C而变到A,则称为“缩”,统称为放缩法,放缩法是一种技巧性较强的不等变形,关键是放、缩适当,跨度合理,放不能过头,缩不能不及.
(2)裂项放缩:在证明数列不等式中涉及数列求和时,经常出现这类技巧.
放缩法常用的结论如下:
❶ ![]()
❹ 绝对值不等式:||a|-|b||≤|a±b|≤|a|+|b|.
(3)并项放缩:有些不等式问题,直接放缩无法办到,如果对原不等式中的项进行适当重组,可使原问题出现“柳暗花明又一村”的境地,并项放缩是局部调整法最为简单的一种.G·波利亚也说过“局部提示整体”,局部调整,分段逼近是导致不等式证明,特别是数列不等式证明得以解决的重要解题策略.
(4)加强放缩:有些数列不等式问题若直接证明命题比证明其某个加强命题更困难.这时,我们不妨“欲擒故纵”,先通过证明原命题的某个“更强的命题”,从而“顺手牵羊”地解决原命题,这种证明方法称为加强命题法,这是证明数列不等式问题的一种有效方法.
总之,有关不等式的证明,在对问题作细致观察的基础上,展开丰富的联想、开启创造性思维的大门,将待处理的问题变化(转化)为目标模式或规范问题,从而使原问题得到解决,是化归思想的体现,运用放缩法证明不等式,其实质是化归思想的运用.
一、例题精讲
例1 设a、b、c均为非负实数,求证:
解题策略 运用基本不等式证明不等式有时会出现“放缩过头”的状况,使证明陷入僵局,如用a2+b2≥2ab,则有![]() 同理
同理![]() 于是有
于是有![]() 而实际上,
而实际上,![]() 可得
可得![]() 两者矛盾,说明上述用a2+b2≥2ab来缩小a2+b2有点过头,所以用放缩法变形应当把握好放缩的尺度,注意“适度”.
两者矛盾,说明上述用a2+b2≥2ab来缩小a2+b2有点过头,所以用放缩法变形应当把握好放缩的尺度,注意“适度”.
证明 由a2+b2≥2ab,得2(a2+b2)≥(a+b)2,即![]()
也即![]() 同理可得
同理可得![]()
∴![]()
例2 若n是正整数,求证:![]()
解题策略 本不等式左边项数很多,不能直接通分,要通过适当放缩才能得出证明.可利用![]() 进行放大再裂项实施.
进行放大再裂项实施.
证明 ![]()
例3 已知:a,b,c,d都是正数.
求证:![]()
解题策略 与上例类似,本题不能直接通分,只有采用放缩法,即分母放大分数值缩小,且用![]() 放大,方可获证.
放大,方可获证.
证明 
又由![]() 可得
可得
∴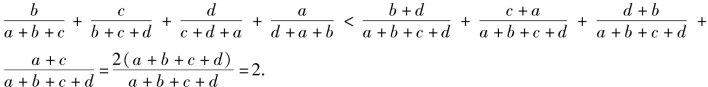
综上,![]() 得证.
得证.
例4 已知:数列{an}满足![]() 是{an}的前n项的和,a2=1.
是{an}的前n项的和,a2=1.
(1)求Sn;
(2)证明:![]()
解题策略 第(1)问,通过累乘法求通项an,再求前n项和Sn;第(2)问,通过二项展开式直接放缩.注意放缩的跨度,放不能过头,缩不能不及.
解:(1)当n≥2时,有
②-①得(n-1)an+1=nan,即![]()
![]() 又
又![]() 得a1=0,故
得a1=0,故![]()
(2) 因此,
因此,![]() (当n=1时取等号).
(当n=1时取等号).
另一方面,易证![]()
则![]()
因此,有![]() 当n=1时,
当n=1时,![]() 左边等号成立.
左边等号成立.
例5 已知:各项均为正数的数列{an}的前n项和为Sn,且![]()
(1)求证:![]() (https://www.xing528.com)
(https://www.xing528.com)
(2)求证:![]()
解题策略 第(1)问,运用基本不等式放缩;第(2)问,放缩后构造成等差数列求和.
证明 (1)在条件中,令n=1,得![]()
又由条件![]() 有
有![]() 将这两式相减,
将这两式相减,
∵an+1=Sn+1-Sn,有(an+1+an)(an+1-an-1)=0.
∵an>0,∴an+1+an>0,故an+1-an=1.
(2)![]()
例6 已知数列{an}满足![]()
求证:![]()
解题策略 运用累加法结合放缩法证明.
证明 ![]() 与an同号,又∵a1=1>0,∴an>0,
与an同号,又∵a1=1>0,∴an>0,
即![]() 即an+1>an,∴数列{an}为递增数列.
即an+1>an,∴数列{an}为递增数列.
∴an≥a1=1,即![]()
运用累加法得:![]()
令![]()
错位相减得:![]()
![]() 由
由![]() 得
得![]()
故得![]()
例7 已知![]() 且1<x1<2.
且1<x1<2.
(1)当n≥2时,求证:![]()
(2)试确定一个正整数N(N≥2),使得当n>N时,都有![]()
解题策略 第(1)问,探究数列的单调性得到一个不等式模型依次放缩,逐步通向结论;第(2)问,将通项依等比递缩的形式进行放缩持续靠近目标.
解:(1)![]()
![]() 从而
从而![]()
又当1<x1<2时,有![]() 故x2是x1∈(1,2)上的递减函数.
故x2是x1∈(1,2)上的递减函数.
![]() 同理可得
同理可得![]()
易知x3是![]() 上的递减函数,且
上的递减函数,且![]() 由此依次迭代可得
由此依次迭代可得![]()
(2)因为![]()
当n=0时,有![]() 由此可得,当取N=6时,能使得当n>N时,都有
由此可得,当取N=6时,能使得当n>N时,都有![]()
二、发散训练
1. 求证:![]()
2. 已知数列{an}满足![]() 且
且![]()
(1)求证:![]()
(2)设数列![]() 的前n项和为Sn.求证:
的前n项和为Sn.求证:![]()
3. 设数列{an}满足![]()
(1)当a1=2时,求a2,a3,a4,并由此猜测出an的一个通项公式(不需要证明);
(2)当a1≥3时,用数学归纳法证明an≥n+2;
(3)当a1=3时,求证:![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




