高中数学压轴题攻略：构造思想与构造法

构造法是高中数学学习中一种极其重要的思维方法与学科方法，通过对数学问题的已知条件和结论进行深入分析，抓住问题的本质特征，恰当地构造辅助元素或数学模型，转化原问题的结构，重组条件和结论之间的关系，产生一种新的结构，通常这种新结构的构思精巧、联想丰富、思维灵活，通过构造所得新问题的解决出奇制胜地解决了原问题.

构造法又可以分为直接构造法和间接构造法.

直接构造法的作用是通过构造具体实例，使所研究的数学对象及其特性的存在得以肯定，或者通过构造反例否定所研究的数学对象或其特性的存在.一旦构造成功，结论也就一目了然，一般来说，直接构造法的知识体系没有改变.

构造的对象不仅仅是直接导致结论肯定和否定的实例，还包含有辅助工具，通过辅助工具使问题得以顺利解决，这就是间接构造法.构造的工具是多种多样的，按它的内容可以分为数、式、函数、方程、数列、向量、图形、图表、计算程序、数学模型等.掌握间接构造法的关键在于审时度势，积极展开想象，灵活运用所学的数学基础知识.间接构造法常常会打破原有的知识体系，转化为另一个知识体系中的数学问题.

构造法是一种极富技巧性和创造性的解题方法，并不是“无中生有”，构造必有源头，也并不是高不可攀，而是敏锐的洞察能力发挥作用的结果.构造法是一种具有创造性的解题方法，体现了函数与方程、数形结合、转化与化归的思想，渗透着猜想、实验、归纳、类比、特殊化等数学方法，注重解题时敢于打破常规、知识前后之间的联系与迁移、新旧知识之间的类比与转化、融合与贯通，总之，构造思想与构造法是攻克压轴题的锐利武器，必能让我们击穿壁垒，大获全胜.

一、例题精讲

例1　(2018年高考数学上海卷第12题)

已知实数x1、x2、y1、y2满足则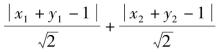的最大值为________.

解题策略　本题初看条件比较多，要求的代数式又带绝对值符号，似乎有点复杂，但是我们仔细观察条件和结论中各式的特点，构造图形来解应当是首选.由我们发现点P(x1，y1)、Q(y2，y2)在单位圆x2+y2=1上.而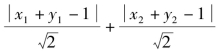正是P、Q两点到直线x+y-1=0的距离之和，条件x1x2+y1y2正好是即可知与的夹角为再进一步思考，其中还隐藏着许多信息，可以通过不同的角度去构造图形或关系式求解.

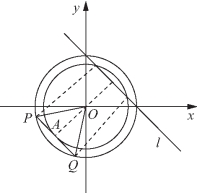
　图2-8

解法一　如图2-8所示，由题意知P(x1，y1)，Q(x2，y2)在单位圆x2+y2=1上，且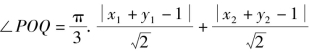表示P、Q两点到直线x+y-1=0的距离之和，设PQ的中点为A，A到直线x+y-1=0的距离为d.

则根据梯形的中位线定理，得

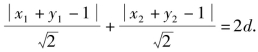
在△OPQ中，的轨迹是以O为圆心为半径的圆.当OA⊥l时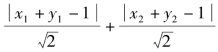，的最大值为

解法二　设P(x1，y1)，Q(x2，y2)，由题意知A,B两点在单位圆x2+y2=1上，令x1=cosα，y1=sinα；x2=cosβ，y2=sinβ，(α、β∈[0，2π)且α>β).

由可得即

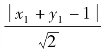和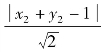分别表示点A,B到直线x+y-1=0的距离，要使上述距离的和最大，A,B两点应在直线x+y-1=0的左下方区域，此时x1+y1-1<0，x2+y2-1<0.

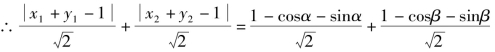
显然当即时，上式有最大值

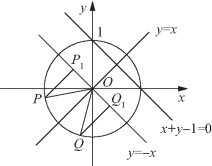
　图2-9

解法三　如图2-9所示，由题意知，点P(x1y1)，Q(x2，y2)在单位圆x2+y2=1上且满足(O为原点)，所求最大值为P、Q两点到直线x+y-1=0的距离之和的最大值.为了充分利用单位圆简化运算，作直线y=-x，作PP1垂直于y=-x，垂足为P1，作QQ1垂直于y=-x，垂足为Q1,则

所求的最大值在PP1+QQ1的最大值的基础上再加上两条平行线距离的两倍即可，即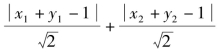的最大值为

解法四　(将已知条件放缩后用基本不等式求解，基本不等式a2+b2≥2ab可变形得(a+b)2≤2(a2+b2)，即

易证2x1y1+2x2y2的最大值为1，因此有

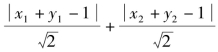
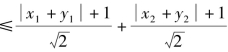
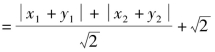
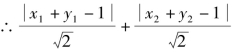的最大值为

例2　(2016年高考数学四川卷理科第10题)

在平面内，定点A、B、C、D满足动点P，M满足则的最大值是(　　).

解题策略　本题考查向量的概念与运算，由于条件中可以深入挖掘其内在的几何意义，如何构造符合题意的图形求解就显得非常重要，不同的构造可以运用不同的知识来求解，虽是小题，容量却相当大.

解法一　由知，D为△ABC的外心，由知，D为△ABC的内心.

∴△ABC为正三角形，D为正△ABC的中心.且以BC所在直线为x轴，其中垂线为y轴建立平面直角坐标系，则有由知M为线段PC的中点.设M(x，y),则

由得即点M的轨迹为圆圆心为

于是|BM|的最大值为故的最大值是故选B.

解法二　由知，点A，B，C在以点D为圆心的圆上，设圆的半径为r，由得

r2cos∠ADB=r2cos∠BDC=r2cos∠CDA=-2,　①

∴∠ADB=∠BDC=∠CDA=120°，代入①式得r=2.

以点D为原点，DA所在直线为x轴建立平面直角坐标系，如图2-10所示，易求得

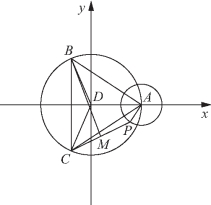
　图2-10

由知，动点P在以点A为圆心,半径为1的圆上，故可设P(2+cosθ，sinθ),又由知，点M为PC中点.

而

故选B.

例3　已知求的最大值.

解题策略　本题求代数式的最大值.由于代数式中含两个字母，若用消元法，代数式更为复杂，且根式还在，求其最大值很难办到.解题的关键是首先应考虑化无理为有理，若按三角函数方向移植，可以有如下的解法：由a>0，b>0，且得

故可设代入已知，解得

∴a2+b2

至此，完成了对a2+b2的化简，即求出了实现了化无理为有理的目的，即那么如何求它的最大值呢？显然并不容易办到，需要进一步挖掘内在的含义.

可见，对数学问题的构造，方向要对头，方向不对常会使问题的解答陷入死胡同.方向对，则问题迎刃而解.

进一步观察的结构，显然是Rt△AOB的内切圆的直径.因此，原问题相当于求Rt△AOB内切圆的直径的最大值，那么条件又是什么呢？如果将变形为可见是直线过定点

则求代数式的最大值问题移植为几何问题.由于a、b为变量且a>0，b>0，若引进角参数，则原问题又可构造为三角函数最值问题.(https://www.xing528.com)

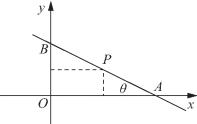
　图2-11

解：将变形，得可见直线过定点如图2-11所示，显然有

其中所以,

故

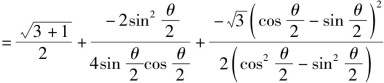
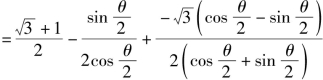
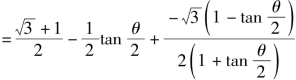
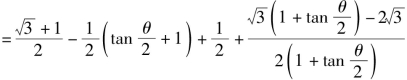
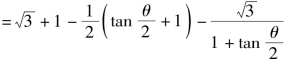
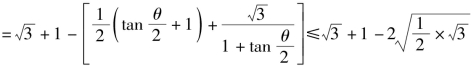
当且仅当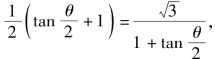即时，取得最大值

例4　设f(α)=sinxα+cosxα，x∈{n|n=2k，k∈N*}，利用三角变换，估计f(α)在x=2,4,6时的取值情况，进而对x取一般值时对f(α)的取值范围作出一个猜想并证明.

解题策略　本例是归纳—猜想—证明类题型，当x=2、4、6时利用三角变换容易求出f(α)的取值范围，则对x取一般值时，很难用三角变换作进一步探索，故在获得猜想之后如何进行证明应考虑采用构造法.一是把三角函数的取值范围问题移植为代数函数的取值范围问题，用导数解决或由图像的凹凸性解决、函数性质和不等式知识在证明中起主导作用.二是通过构造运用二项式定理结合三角函数有界性求f(α)的范围或直接运用基本不等式等放缩的技巧.

解：逐一计算：当x=2时，f(α)=sin2α+cos2α=1.

当x=4时，

可得即

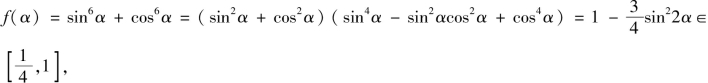当x=6时，即

……

由此猜想：当x=2k(k∈N*)时，f(α)的取值范围为

证法一　(构造函数，用导数解决)

设函数g(x)=xk+(1-x)k，0≤x≤1，k≥2.

则g′(x)=kxk-1-k(1-x)k-1=k[xk-1-(1-x)k-1],可以判断：

g(x)在区间上递减，在区间上递增，

故当时，

又∵g(0)=g(1)=1为最大值，故g(x)的值域为

令x=sin2α，α∈R，可得

证法二　(构造函数，用图像的凹凸性解决)

构造函数g(x)=xk(0≤x≤1，k≥2)，g′(x)=kxk-1，g″(x)=k(k-1)xk-2>0对任意0<x<1恒成立.

故g(x)=xk(0≤x≤1)为下凸函数，它在点处的切线方程为

即

由图像的凹凸性可知，函数g(x)=xk(0≤x≤1)的图像总在切线的上方(或重合)，故有对任意0≤x≤1恒成立

对于α∈R，有0≤sin2α≤1,0≤cos2α≤1，用sin2α，cos2α分别代替x可得

　①

　②

①+②，得

另一方面，由0≤sin2α≤1,0≤cos2α≤1可得

f(α)=sin2kα+cos2kα=sin2k-2α·sin2α+cos2k-2α·cos2α≤sin2k-2α+cos2k-2α≤…≤sin2α+cos2α=1，即

证法三　(构造二项式定理，用放缩法)

f(α)

=

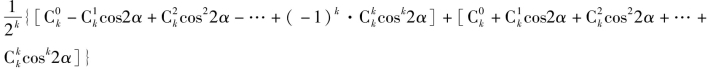
当cos2α=0时，

当cos2α=±1时，

故

证法四　(构造并运用基本不等式进行放缩或构造二项式实现放缩)

y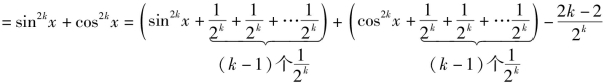

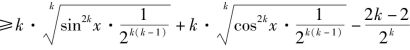
等号成立即当时，此时ymin=21-k.

另一方面，又∵sin2kx+cos2kx≤(sin2x+cos2x)k=1，等号成立⟺sinxcosx=0，此时ymax=1.

故函数y=sin2kx+cos2kx(k∈N*)的值域是[21-k,1].

二、发散训练

1.(1)求证：

(2)已知a>b>0，求证：

(3)已知a，b∈R+，且a+b=1，求证：

2.(1)若且满足方程：x3+sinx-2a=0和4y3+sinycosy+a=0，求cos(x+2y)的值；

(2)已知α、β为两相异锐角，且满足方程acos2x+bsin2x=c，求证：

3.(1)试求函数的最大值；

(2)求二元函数的最小值.