巧用圆锥曲线方程：高中数学微专题解题攻略

应用曲线系方程解题，即引入适当的参数先设出符合部分条件的曲线系方程，然后根据题中的其他条件，通过推理、运算求出曲线系方程中的参数值，从而实现问题的解决.运用曲线系方程往往可以回避联立解方程组、求交点坐标等带来的麻烦，既减少了计算量，又体现了参数变化、整体处理、待定系数法等重要的数学思想方法.当然，由于曲线系方程的多样化、所给问题条件的隐蔽性，应用曲线系方程解题虽然减少了运算量，但对技巧的要求颇高，在高中数学竞赛中运用较为广泛，本讲对各类圆锥曲线系方程进行归纳总结.

圆锥曲线系方程：

(1)共顶点圆锥曲线系方程：(λ为参数).

(2)共渐近线双曲线系方程：(λ为参数，λ≠0).

(3)共焦点圆锥曲线系方程：(c为焦半径，λ为参数).

当λ>0时，表示共焦点椭圆系；当-c2<λ<0时，表示共焦点双曲线系；当λ<-c2时，无轨迹.

(4)共离心率圆锥曲线系方程：(λ为参数，λ>0).

(5)过两圆锥曲线4个交点的圆锥曲线系：

若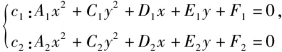是有4个交点的二次曲线，则c：A1x2+C1y2+D1x+E1y+F1+λ(A2x2+C2y2+D2x+E2y+F2)=0是过c1、c2的交点的圆锥曲线系，其中不包括c2(λ为参数).

(6)过两条直线与圆锥曲线4个交点的圆锥曲线系：

若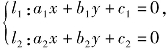与圆锥曲线c：Ax2+Cy2+Dx+Ey+F=0有4个交点，则方程Ax2+Cy2+Dx+Ey+F+λ(a1x+b1y+c1)(a2x+b2y+c2)=0为过4个交点的圆锥曲线系方程.

一、例题精讲

例1　(1)求渐近线方程为3x±4y=0，焦点为椭圆的一对顶点的双曲线的方程；

(2)求与双曲线有共同的渐近线，且与直线5x-6y-8=0相切的标准双曲线方程.

解题策略　当已知双曲线的渐近线方程为(或y=±mx)时，可设双曲线的方程为或m2x2-y2=λ)(其中λ为不等于零的待定常数)，以简化运算过程，这里方程且λ≠0)称之为与双曲线共渐近线的双曲线系，为解题带来方便.

解：(1)依题意，可设双曲线的方程为(λ是正实数)，当双曲线的焦点为椭圆的长轴的顶点，即与时，由c2=a2+b2,可得∴双曲线的方程为

当双曲线的焦点为椭圆的短轴的顶点，即与时，双曲线的方程为(λ是正实数)，即

∴双曲线的方程为

(2)解法一　(利用共渐近线双曲线系方程结合判别式法)

设所求双曲线的方程为

∵此双曲线与直线5x-6y-8=0相切，且显然其渐近线都不平行于直线5x-6y-8=0.

∴由方程组消去x，得4y2-6y+25λ-4=0，其判别式Δ=(-6)2-4×4×(25λ-4)=0，解得

故所求双曲线的标准方程为即

解法二　(利用共渐近线双曲线系方程结合待定系数法)

设所有双曲线的方程为即x2-4y2=16λ(λ≠0)，

设其与直线5x-6y-8=0相切的切点为(x0，y0)，

则切线方程为x0x-4y0y-16λ=0，∴有代入双曲线方程中并化简得4λ2=λ，又故所求双曲线的标准方程为

解法三　(利用共渐近线双曲线系方程结合双曲线参数方程解)

设所求双曲线方程为双曲线上一点M的坐标为以此点为切点的双曲线的切线方程为化简得

∵它和直线5x-6y=8重合，即由等比定理得即代入原双曲线方程得此即为所求.

例2　讨论方程所表示的曲线.

解题策略　观察方程可以发现其中心在原点，是有心曲线，对称轴为坐标轴，若25-k>9-k>0，则方程表示椭圆系，c2=(25-k)-(9-k)=16，c=4；若则方程表示双曲线系，c2=(25-k)+(k-9)=16，c=4.

所有的曲线焦点相同，因此，原方程表示中心在原点，对称轴为坐标轴、有相同焦点的圆锥曲线系.

解：由所给方程知k≠25且k≠9，原方程可化为

(9-k)x2+(25-k)y2=(25-k)(9-k).

它表示中心在原点，对称轴为两坐标轴的有心圆锥曲线系.

(1)当k<9时，它的曲线是椭圆.

∵c2=a2-b2=(25-k)-(9-k)=16,∴焦点为(-4，0)和(4，0).

(2)当9<k<25时，它的曲线是双曲线.

∵c2=a2+b2=(25-k)+(k-9)=16，∴焦点为(-4,0)和(4,0).

(3)当k>25时，25-k<0，9-k<0，方程无实数解，故方程无轨迹.

因此，原方程表示的是具有同一中心，相同对称轴、相同焦点的有心圆锥曲线系.

例3　已知圆(x-1)2+y2=9和双曲线x2-y2=1，求通过它们的4个交点和点M(0,2)的二次曲线方程.

解题策略　构造过圆与双曲线4个交点的圆锥曲线系，而圆锥曲线系过点M(0,2)，可待定参数的值，从而大大减少运算量.

解：圆方程和双曲线方程可分别写成x2+y2-2x-8=0，x2-y2-1=0，将其中第二个方程乘以任意实数λ，然后与第一个方程相加，得

(x2+y2-2x-8)+λ(x2-y2-1)=0.　①

圆和双曲线的任一交点的坐标同时满足圆方程和双曲线的方程，因而使①式左边两个括号里面代数式的值同时为0，所以这些交点都在①式表示的二次曲线上.

将点M的坐标(0,2)代入①式，得将所得λ值代入①式，得

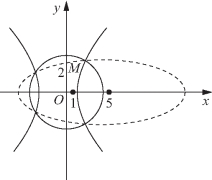
　图2-3

化简得x2+9y2-10x-36=0，即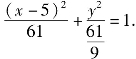所得的曲线是一个椭圆，它的中心是点(5，0)，焦点在x轴上，长半轴和短半轴分别是和如图2-3所示).

例4　一条圆锥曲线过点切直线x-2y+5=0于点(1，3)，切直线5x+2y-20=0于点(4,0)，求它的方程.

解题策略　由于圆锥曲线的形态不清楚，无法直接求解，只能通过圆锥曲线系来解，如何列出符合条件的圆锥曲线系是关键.

解：过点(1，3)、(4,0)的直线方程为x+y-4=0,　①

由于(1，3)、(4,0)都是切点，直线①可以看作是两条重合的直线(退化了的曲线)，于是所求方程可写成(x-2y+5)(5x+2y-20)+λ(x+y-4)2=0.　②

再由曲线过点代入②式，解得

故所求方程为45x2+18xy+9y2-180x=0.

例5　(1)(蝴蝶定理)过圆AB弦的中点M，任意作两弦CD和EF，CF和ED交弦AB于P、Q，求证：PM=QM；

(2)AB是圆Γ的一条定弦，O为AB上的定点，过点O作圆Γ的两条弦CD和EF，弦CF和OA交于点I，弦DE与OB交于点J.求证：

解题策略　运用曲线系方程证明蝴蝶定理及其推广比用平面几何知识证明要简便许多.

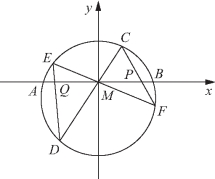
　图2-4

证明　(1)如图2-4所示，以M为原点，AB所在直线为x轴建立直角坐标系，设圆方程为

x2+(y-b)2=r2(|b|<r).

设直线CD、EF的方程分别为y=k1x,y=k2x.将它们合并为(y-k1x)(y-k2x)=0，于是过点C、D、E、F的曲线系方程为

x2+(y-b)2-r2+λ(y-k1x)(y-k2x)=0.

令y=0，得(1+λk1k2)x2+b2-γ2=0,即过点C、D、E、F的曲线系与AB交于点P、Q的横坐标是方程(1+λk1k2)x2+b2-γ2=0的两个根.由韦达定理得xP+xQ=0，即M是PQ的中点，故PM=QM.

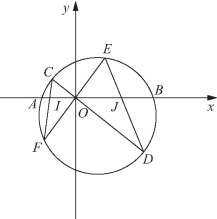
　图2-5(www.xing528.com)

(2)如图2-5所示，以O为原点，直线AB为x轴建立平面直角坐标系，设圆Γ的方程为x2+y2+dx+ey+f=0.

lCD：x-t1y=0,lEF：x-t2y=0.

则直线CD、EF合成的二次曲线方程为(x-t1y)(x-t2y)=0，

从而，经过C、D、E、F这4点的曲线系方程为

x2+y2+dx+ey+f+λ(x-t1y)(x-t2y)=0.　①

∴存在λ，使得①为直线CF、DE合成的二次曲线.

在①中,令y=0，则xI、xJ是方程(1+λ)x2+dx+f=0的两个根.

由韦达定理得

在①中，令λ=0，y=0，则xA、xB是方程x2+dx+f=0的两个根.

由韦达定理得xA+xB=-d，xA·xB=f，又∵xA<0，xB>0，f≠0，

故

例6　已知任意二次曲线S，AB是曲线S的弦，O是AB的中点，过点O任意作弦CD、EF，过点C、D、E、F另作一条任意二次曲线t，如果曲线t与直线AB交于点P、Q，求证：|OP|=|OQ|.

解题策略　上例介绍了平面几何蝴蝶定理的证明和应用,本例是平面几何蝴蝶定理的推广，从圆一步飞跃到任意的二次曲线，联结圆上4点的两直线CF和DE也直接换成一般的二次曲线，从蝴蝶定理的特殊图形里看到一般的二次曲线系，升级换代、一次到位，不是拾级而上，而是直上高楼，美景无限.观察如图2-6所示图形，里面是否隐藏着一只飞舞的蝴蝶？

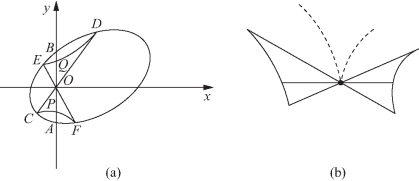
图2-6

证明　如图2-6(a)所示，取直线AB为y轴，O为原点，AB方向为y轴的正方向建立直角坐标系.

设|OA|=|OB|=a，则点A的坐标为(0，-a)，点B的坐标为(0，a).

∵二次曲线S通过点A(0，-a)、B(0，a),

∴在曲线S的方程中，当x=0时，应有y2=a2.因而二次曲线S的方程形如：Ax2+Bxy+y2+Dx-a2=0.　①

又∵弦CD、EF都通过原点O，且与直线AB相交(因而都不是y轴).

∴可设它们的方程分别为y=k1x，y=k2x.

这一对直线CD和FE合在一起，可以看成一条退化二次曲线u.

其方程为(y-k1x)(y-k2x)=0.　②

曲线①和②相交于点C、D、E、F,利用曲线系知识，通过C、D、E、F的二次曲线系的方程为(Ax2+Bxy+y2+Dx-a2)+λ(y-k1x)(y-k2x)=0,　③

若曲线③中的一条二次曲线t交y轴于点P(0，y1)和点Q(0，y2)，

则在③式中以x=0代入，得(1+λ)y2-a2=0,　④

y1和y2应该是所得二次方程④的两个实数根，由二次方程根与系数的关系，得y1+y2=0，∴y1=-y2，即|OP|=|OQ|.

例7　(1)4条直线l1：x+3y-15=0,l2：kx-y-6=0,l3：x+5y=0,l4：y=0围成一个四边形，问k取何值时，该四边形有一个外接圆，并求出外接圆的方程；

(2)已知椭圆C1：x2+9y2-2x-36y+27=0与双曲线C2：4x2-y2+2y-5=0有4个交点，求证：此4个交点共圆，并求出此圆的中心坐标.

解题策略　第(1)问，用直线方程交点构成的二次曲线系方程求解；第(2)问，用过两圆锥曲线交点的二次曲线系方程求解或证明.

解：(1)设过该四边形4个顶点的二次曲线系方程为

(x+3y-15)(x+5y)+λ(kx-y-6)·y=0，

即x2+(8+kλ)xy+(15-λ)y2-15x+(-75-6λ)y=0,

由解得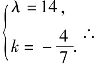所求圆的方程为x2+y2-15x-159y=0.

(2)证明　设过C1和C2交点的曲线系方程为x2+9y2-2x-36y+27+λ(4x2-y2+2y-5)=0(不包括C2)，即(1+4λ)x2+(9-λ)y2-2x-(36-2λ)y+27-5λ=0.

显然，当1+4λ=9-λ，即时，曲线系方程表示一个过C1和C2交点的圆.

将代入曲线系方程化简得：37x2+37y2-10x-164y+95=0，

即椭圆与双曲线的4个交点共圆.

不难得到此圆的中心坐标即圆心坐标为

例8　求过(0，0)，(1，1)，(-1，1)，(2，0)，(3，-2)这5点的二次曲线方程.

解题策略　写出过其中4点的二次曲线系，用第5点的坐标代入确定参数的值.

解：过O(0，0)、C(2,0)的直线方程为y=0，过A(1，1)，B(-1,1)的直线方程为y=1，两者合并为y(y-1)=0.

直线OB的方程为x+y=0,直线AC的方程为x+y-2=0，两者合并为(x+y)(x+y-2)=0.

因此，过A、B、C、O这4点的二次曲线系方程为y(y-1)+λ(x+y)(x+y-2)=0.

所求二次曲线必须经过点D(3，-2).

代入解得λ=6，从而所求二次曲线方程为y(y-1)+6(x+y)(x+y-2)=0.

即6x2+12xy+7y2-12x-13y=0.

例9　已知点B(0,1),P、Q为椭圆上异于点B的任意两点,且BP⊥BQ.若点B在线段PQ上的射影为M,求点M的轨迹方程.

解题策略　在运用曲线系方程解题时，曲线系方程中包含着一些特殊情况，如本题中设出经过B、P、Q三点的曲线系，其中包含椭圆在点B处的切线和直线PQ，这点务必请注意到.

解：易知直线BP、BQ的斜率均存在且不为0，

设

则经过B、P、Q3点的曲线系方程为

　①

即其中包含过点B的椭圆的切线y=1.

　图2-7

方程左边多项式中必含有因子(y-1)，把y=1代入①式得而x不恒等于0，故即λ=-4，此时即

∴直线PQ的方程为即PQ恒过定点

如图2-7所示，由∠BMN=90°知，点M的轨迹是以线段BN为直径的圆(除去点B).

∵kBM·kMN=-1,即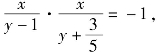

∴其方程为即

二、发散训练

1. 求与抛物线y2=5x+9相切于点P(0，3)、Q(-1，-2)两点，且过点A(-2，1)的圆锥曲线方程.

2. 设A、B是双曲线上两点，N(1，2)是线段AB的中点，线段AB的垂直平分线交双曲线于C、D两点.

(1)确定实数λ的取值范围；

(2)试判断A、B、C、D4点是否共圆？说明理由.