递推数列通项拓展方法

对于递推数列求通项类题型，虽然在数学教学中的要求不是很高，高考命题时难度也有控制，但是在原名牌大学自主招生时，递推数列则是一个重要考点，解题方法更丰富多彩，对于将要实施的“强基计划”来说想必也是重要考点.本讲介绍两种递推数列求通项的新方法.

1.特征根法

型如a1=m1，a2=m2，an+2=pan+1+qan(p、q是常数)的数列为二阶线性递推数列，可构造{an+1-λan}，满足an+1-λan=μ(an-λan-1)，则即λ、μ为方程x2-px-q=0的两个根，此方程称为特征方程，则数列{an}的通项公式an均可用特征根转化为一阶线性递推数列，进一步构造特殊数列或利用“累加法”求通项公式.

2.不动点法

型如的递推式，可利用不动点法，其中的根为该数列的不动点，若该数列有两个相异的不动点μ、v，则为等比数列；若该数列有唯一的不动点μ，即方程等根时，为等差数列，这就是不动点求递推数列通项公式的方法.

例1　已知sinα+cosα=k,求sin5α+cos5α的值.

解题策略　一个数学问题有时候很难一下子得到结果，于是设想把问题分成若干步，找出相邻两步之间的关系，可以达到目的.一般而言，一个与正整数有关的数学问题，由初始值通过递推公式，若能使问题解决，则这种解题方法称为递推方法，本题中初始值是sinα+cosα=k，但没有给出递推式，如果能够找到递推式，则sin5α+cos5α的值就容易求得，而求递推式的过程既有归纳又有推理的逻辑思维过程，这正是递推方法的独到之处.

解：设f(n)=sinnα+cosnα,由(sinα+cosα)2=k2,得

∵(sinnα+cosnα)(sinα+cosα)=sinn+1α+cosn+1α+sinαcosα(sinn-1α+cosn-1α)，

又

以此类推，可得即

例2　(1)数列{an}满足a1=1，a2=11，an+2=2an+1+3an+4(n∈N*)，求通项an；

(2)数列{an}满足求通项an；

(3)数列{an}满足求通项an.

解题策略　第(1)问,可运用特征根法，当然由于所给递推式并非是规范的二阶线性递推数列，首先要适当变形使之符合类型，再运用这一方法求解；第(2)、(3)两问，可运用不动点法.

解：(1)由an+2=2an+1+3an+4,得an+2+1=2(an+1+1)+3(an+1).

不妨设bn=an+1，则bn+2=2bn+1+3bn.其特征方程为x2-2x-3=0，特征根为x1=3，x2=-1.

故可设bn=c1·3n+c2·(-1)n(c1，c2为待定常数).

由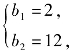则解得

可得从而

(2)设函数解方程f(x)=x，即得

由于　①

　②

且an≠3(否则由②式可以得到a1=3，矛盾).

∴将①②两式相除，得

结合初始条件及等比数列的通项公式，可知

即

(3)设函数解方程f(x)=x，即得x1=x2=2.

由于　③

且an≠2(否则由③式可以得到a1=2，矛盾).

∴两边取倒数，得

数列为等差数列，得从而

例3　已知数列{an}、{bn}满足an+1=-an-2bn，且bn+1=6an+6bn，又a1=2，b1=4，求：

解题策略　观察题设条件，把两个关系式适当变形后代入消元可得到数列{an}的二阶线性递推关系，则可运用特征方程求通项公式.(www.xing528.com)

解：(1)∵a1=2,b1=4,∴a2=-a1-2b1=-2-8=-10，

由an+1=-an-2bn，得an+1+an=-2bn,即

代入bn+1=6an+6bn，得整理得an+2=5an+1-6an，其特征方程为x2-5x+6=0，解之得x1=2，x2=3.

an=c1·2n-1+c2·3n-1，由得解得

(2)

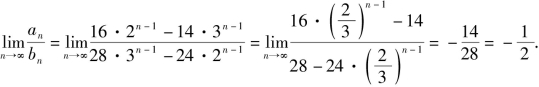
例4　设函数且存在函数满足

(1)证明：存在函数t=φ(s)=cs+d(s>0)满足

(2)设x1=3，xn+1=f(xn)，n=1，2，…，证明：

解题策略　第(1)问，主要运用函数的对应法则与待定系数法证明；第(2)问，运用不动点法求数列的通项再证明.

证明　(1)

∴

即(m+2)at2+(bm+2b-a)t-b=6at2+(6b+3-2a)t-(2b+1).

上式对一切恒成立，必有

又

由

解得故存在函数φ(s)=3s+1.

(2)由考虑数列的不动点，设为x，

则

　①

　②

有是首项为5，公比为-3的等比数列.

⟺4×3n-1≤|5×(-3)n-1-1|，　③

若n=2k，则|5×(-3)n-1-1|=5×32k-1+1≥4×32k-1，显然成立；若n=2k-1，则4×32k-2≤|5×(-3)2k-2-1|⟺4×32k-2≤5×32k-2-1⟺1≤32k-2，显然成立.

综上所述，不等式③成立.

二、发散训练

1. 有一个n层的台阶，若是每次可上一层或两层，那么共有几种上法？

2.(1)数列{an}中，a1=1，a2=3，3an+2=2an+1+an，求an和

(2)设数列{an}和{bn}满足a0=1，b0=0，且试求{an}的通项公式；

(3)已知a1=2，且求通项an.

3. 已知函数f(x)=x2-4，设曲线y=f(x)在点(xn，f(xn))处的切线与x轴的交点为(xn+1，0)(n∈N*)，其中x1为正实数.

(1)用xn表示xn+1；

(2)若x1=4，记求证：数列{an}成等比数列，并求数列{xn}的通项公式；

(3)若x1=4，bn=xn-2，Tn是数列{bn}的前n项和，证明：Tn<3.