高中数学微专题的压轴题攻略：重要的不等式

1.多元均值不等式

若a1，a2，a3，…，an∈R+，则当且仅当a1=a2=…=an时取等号，其中为a1，a2，a3，…，an的算术平均数,为a1，a2，a3，…，an的几何平均数.

2.柯西不等式

(1)二维形式的柯西不等式：若a，b，c，d都是实数，则(a2+b2)·(c2+d2)≥(ac+bd)2，当且仅当ad=bc时取等号.

(2)一般形式的柯西不等式：若a1，a2，a3，…，an，b1，b2，b3，…，bn都是实数，则当且仅当bi=0(i=1，2，…，n)或时取等号.

3.柯西不等式的向量形式及平面三角不等式

(2)平面三角不等式：设x1、y1、x2、y2∈R，则

4.排序不等式

设a1≤a2≤…≤an，b1≤b2≤…≤bn为两组实数，c1，c2，…，cn为b1，b2，…，bn的任意排列，那么a1bn+a2bn-1+…+anb1≤a1c1+a2c2+…+ancn≤a1b1+a2b2+…+anbn，即反序和不大于乱序和,乱序和不大于顺序和.

当且仅当a1=a2=…=an或b1=b2=…=bn时取等号.

一、例题精讲

例1　证明柯西不等式.

解题策略　证明柯西不等式的方法很多，其中向量法与构造法是高中数学中的常见证法，介绍如下，有利于学生开阔解题思路、提升解题能力.

证法一　(向量法：将平面向量、空间向量推广到n维向量)令则

由于故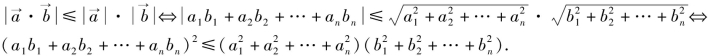等号成立的条件是共线，即ai=λbi(λ∈R).

证法二　(构造二次函数法)若a1=a2=…=an=0，则柯西不等式

显然成立.

若ai不全为零(i=1，2，…，n)，

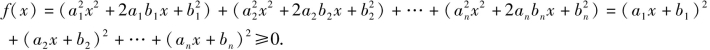令一方面，因为　①

另一方面，由恒成立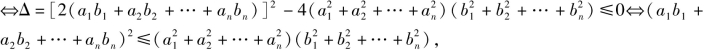此即柯西不等式.

由①式知等号成立的条件为ai=λbi(i=1，2，…，n).

例2　(1)有小于1的n(n≥2)个正数x1，x2，x3，…，xn，且x1+x2+x3+…+xn=1.

求证：

(2)已知a1，a2，…，an∈R+，求证：

解题策略　第(1)问，每一个xi均为(0，1)内的正数，由x1+x2+x3+…+xn=1可联想到均值不等式从而需要对原式中每一项进行放缩，得到x1x2x3…xn乘积的形式，也可构造出柯西不等式的形式，利用柯西不等式来证明.第(2)问，同样可以运用上述两种证法，在运用均值不等式时首先需要对所证不等式通过拆分、构造、再合成的过程.(www.xing528.com)

(1)证法一　(均值不等式法)

又

证法二　(柯西不等式法)　由柯西不等式可得

又

又

(2)证法一　(均值不等式法)

上述不等式相加，即得

证法二　(柯西不等式法)　由柯西不等式可得

例3　已知a，b，c为正数，且a≥b≥c，求证：

解题策略　运用排序不等式解题，首先要把两个数组的大小关系明确出来，分清顺序和、乱序和及反序和，由于乱序和是不确定的，根据需要写出其中的一个即可.

证明　

由顺序和≥乱序和得　①

又

由乱序和≥反序和得　②

由①②两式得

二、发散训练

1.(1)已知a，b，c∈R，a+2b+3c=6，则a2+4b2+9c2的最小值为　　　　；

(2)设x，y，z∈R，且满足：则x+y+z=　　　　.

2.(1)求使直线xcosθ+ysinθ=2和椭圆x2+3y2=6有公共点的θ的取值范围(0≤θ≤π)；

(2)已知直线y=(1-x)tanθ与双曲线-x2+y2cos2θ=1相切求切线方程和切点坐标.

3.(1)设a>0，b>0，求的最小值；

(2)已知x，y，z>0，a，b，c为x，y，z的一个排列，求证：