李正兴高中数学微专题——压轴题攻略

当前数学教育改革和高考改革在不断深入、文理合卷、全国大多数省市统一命题的运作已经开启，教材在不断变化,并且还将迎来新的变革，新的内容在逐渐增加，老的内容有些是减弱了,在理念、内容、思想方法上都有了较大的变化，从而也使得原有课程的知识板块发生了改变，如平面向量已引入许多年，且与三角函数、解析几何知识的交汇与综合一直在加强之中，大量删减了立体几何的许多定理，强调了空间向量在研究空间图形中的作用，而旋转体知识又完整地出现在教材之中，导数的综合应用在加强.随着高考数学命题的不断改革以及数学核心素养作为数学教育的标杆，考纲必然也会随之调整，而且调整幅度会加大，这也是统一命题和文理合卷的大变动所决定的.考题的阅读量会增加，题型也会变化并朝探究型、创新型方向发展，这些都要引起足够的重视.

但有一点是肯定的，不管高考数学命题如何改革，高中数学中的重要板块如函数与导数板块、数列板块、解析几何板块仍然是命题的重点所在，不管是全国卷还是省市卷，作为压轴题必定出现在这些板块中.教材体系就是如此，谁也改变不了.这些板块之间，这些板块与其他数学知识之间的交汇、交叉、结合在较长一段时间内仍然是高考命题的热点.回顾近年来出现的那些最具冲击力的“创新”试题，往往在我们的意料之外，却又在情理之中，脱离不了这些重要板块.

综上所述，在二轮复习过程中，特别在冲刺压轴题的战斗中，不应平分力量，而应在这些重要板块上多花点工夫，集中兵力、“攻城略地”！

一、例题精讲

例1　已知

(1)若m=0，试研究函数在区间上的单调性；

(2)若tanx=2，且试求m的值.

解题策略　本例以向量为载体，注重三角恒等变形、三角函数图像与性质的研究，是向量与三角综合问题中的基本模型之一，也是高考中常见的基本问题.第(1)问，先把函数化简为y=Asin(ωx+φ)+B的形式，再结合区间上的单调性分类讨论；第(2)问，由且通过变形得m与tanx的关系，而tanx=2已知，则m的值即可求得.

解：(1)当m=0时，f(x)

由得

当即时，函数f(x)单调递增；

当即时，函数f(x)单调递减.

(2)由可得

由tanx=2，可得若则此时tanx=-1与条件矛盾).

从而有即m(sinx-cosx)=sinx，两边同除以cosx，可得m(tanx-1)=tanx=2，∴m=2.

图1-25

例2　如图1-25所示，已知动圆与直线y=-3相切，并与定圆x2+y2=1相内切.

(1)求动圆圆心P的轨迹C的方程；

(2)过原点作斜率为1的直线交曲线C于P1(P1为第一象限点)，又过P1作斜率为的直线交曲线C于P2，再过P2作斜率为的直线交曲线C于P3，……如此继续，过Pn作斜率为的直线交曲线C于Pn+1，设Pn(xn,yn).

1令bn=x2n+1-x2n-1，求证：数列{bn}是等比数列；

2数列{bn}的前n项和为Sn，试比较与的大小.

解题策略　本例以解析几何为载体，重点突出数学归纳法的应用，感知“观察—归纳—猜想—证明”的思考与解决的过程，体验其中所呈现的数学美.

解：(1)由题意知，P点到原点的距离等于P点到直线y=-2的距离.由抛物线定义知，P点轨迹是以原点为焦点，直线y=-2为准线的抛物线，其轨迹方程为x2=4(y+1).

(2)1设Pn(xn,yn)，Pn+1(xn+1,yn+1)，则

又因为直线PnPn+1的斜率为有

即

∴bn

∴数列{bn}是以为公比的等比数列.

2由 1 知,

下面只要比较4n与3n+10的大小.

当n=1时，4<13，有4n<3n+10，即

当n=2时，16=16，有4n=3n+10，即

当n=3时，64>19，有4n>3n+10，即

猜测当n≥3时，n∈N时，4n>3n+10.

证法一　用数学归纳法证明当n≥3，n∈N时，4n>3n+10.

(i)当n=3时，已成立；(www.xing528.com)

(ii)假设当n=k(k≥3,k∈N)时，4k>3k+10.

则当n=k+1时，4k+1=4·4k>4(3k+10)=[3(k+10)+10]+9k>3(k+1)+10,

即n=k+1时，4n>3n+10也成立.

由(i)(ii)知,4n>3n+10对n≥3,n∈N都成立.故此时，

证法二　利用二项式定理，得

例3　已知f(x)在(-1,1)上有定义，且满足x,y∈(-1,1)时，有

(1)证明：f(x)在(-1,1)上为奇函数；

(2)数列{xn}满足设an=f(xn)，求{an}的通项公式；

(3)求证：

(4)证明等式

解题策略　本例将函数、数列、不等式等代数知识集于一题，是考查分析问题和解决问题核心素养的范例，在求解过程中，化归为数列模型以及运用数学归纳法证明数列不等式是常用的解题方法.

解：(1)f(x)+f(-x)=f(0)，f(x)+f(0)=f(x)，故f(0)=0，得f(x)+f(-x)=0，故为奇函数.

(2)又故an=-2n-1.

(3)

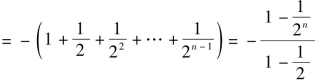
而

故

(4)证法一　(数学归纳法)

(i)当n=1时，左边右边；

(ii)假设n=k时有，

则n=k+1时，左边=

成立.

由(i)(ii)可知，对一切n∈N*,所证不等式成立.

证法二　由条件得

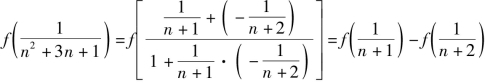
代入所证等式的左边即可.

二、发散训练

1. 随机将1，2，…，2n(n∈N*，n≥2)这2n个连续正整数分成A、B两组，每组n个数，A组最小数为a1，最大数为a2，B组最小数为b1，最大数为b2，记ξ=a2-a1，η=b2-b1,

(1)当n=3时，求ξ的分布列和数学期望；

(2)令C表示事件“ξ和η的取值恰好相等”，求事件C发生的概率P(C)；

(3)对(2)中的事件表示C的对立事件，判断P(C)和的大小关系，并说明理由.

2. 已知二次曲线Ck的方程：

(1)分别求出方程表示椭圆和双曲线的条件；

(2)若双曲线Ck与直线y=x+1有公共点且实轴最长，求双曲线方程；

(3)m、n为正整数，且m<n，是否存在两条曲线Cm、Cn，其交点P与点满足若存在，求m、n的值；若不存在，说明理由.