一道高考数学压轴题通常涉及多个知识点,需要调动多种解题方法联合作战,所以我们不仅要对每个知识点理解透彻,而且要打通知识点之间的连接,构建知识网络,把点拓展成线,扩充为面,许多压轴题都是在多种知识的交汇处命制.如果你对此没有充分的认识,你就调动不了多个知识为你所用.光能调动知识还不足以使问题顺利解决,还需要精准的解题策略指引.按照G·波利亚的解题理论,面对题目,在弄清问题、拟定计划之后,应当进入实现计划与回顾反思阶段.若你的解题计划是完善的,实现计划往往是“例行公事”,但事实上任何计划不可能100%的完善,难免需要作出少量的修改.在实现计划的过程中一般需要作一些机械性的计算和推理,如果在一个细节上出了问题,还得推倒重来,所以在实现计划的过程中关注细节非常重要.细节决定成败,这种例子在数学解题中是很多的.
题目是解好了,解答是否完备呢?这也需要解题者回顾反思.G·波利亚指出:“通过回顾完整的答案、重新斟酌、审查结果及导出结果的途径,他们能够巩固知识,并培养他们的解题能力.”讲的便是“解后思”,即回顾反思的重要性.在完成解题过程之后,有时候感到很满意,有时候也会感觉到不够满意,似乎使用的解题方法是笨办法,解题步骤太烦琐,明明可以有一种较为简捷的解法,当时没有想到,没有做到直剖核心,快速中的,等等.又或者,你的解题方法完全正确,没有更快捷的解法了,然而解题过程中有些地方走了弯路,书写不够科学规范,有几步是多余的,删除多余的可以更完美.正如G·波利亚所说,回顾反思是“领会方法的最佳时机”“当读者完成了任务,而且他的体验在头脑中还是新鲜的时候,去回顾他所做的一切,可能有利于探究他刚才克服困难的实质,他可以对自己提出许多有用的问题:‘关键在哪里?重要的困难是什么?什么地方我可以完成得更好些?我为什么没有觉察到这一点?要看出这些我必须具备哪些知识?应该从什么角度去考虑?这里有没有值得学习的诀窍可供下次遇到类似问题时应用?’所有这些问题都提得不错,而且还有许多别的问题——但最好的问题是自然而然地浮现在你脑海里的问题.”
坚持回顾反思,可以使你通过解决一道题达到能顺利解决一批题的能力,这叫作举一反三甚至举一反十.
坚持回顾反思,可以养成一种敏锐的“题感”,碰到众多的同类问题,脑海里顿时思路涌动,解题时,迅速抓住关键,单刀直入,立即深入问题的核心,解题高手就是在不断地回顾反思中炼成的.
以点带面、直剖核心,这种解题真功夫知识层面的梳理贯通需要解题战略战术的引领,需要数学思想的引领,需要发散思维品质的提升.G·波利亚说:“解答一个题目的主要成就在于构思一个解题方案.”我认为G·波利亚的说法可作这样的改变,即“解答一个题目尝试构思若干个解题的方案”,如何构思解题方案呢?由于看同一个问题的角度可以不同,脑海里涌现出来的相关知识点也会不同,而知识之间常常是交错连接,互相渗透,于是各种思路就会涌现出来,一题多解也就产生了,所以学生在复习的过程中首先要把知识点梳理清楚,构建知识网络图,然后逐步学会从不同的角度看待同一个问题,寻求解决问题的多种途径,尝试采用若干不同的解法,再进行比较研究.当然各种解法或简捷或繁杂、或直接或曲折,要找出最为简明的解法,当然也有可能一个问题的不同解法各有妙处、自成体系、难说谁优谁劣.总而言之,善于发散思维,掌握一题多解是攻克压轴题的实战演习,也是解题能力的升华.
福建师范大学数学教授卢正勇先生在“怎样提高解题能力”一文中提出的解题程序用以下的框图表示,完全可以与G·波利亚的怎样解题四部曲(四大环节)对照起来看,两者的内在是完全一致的.
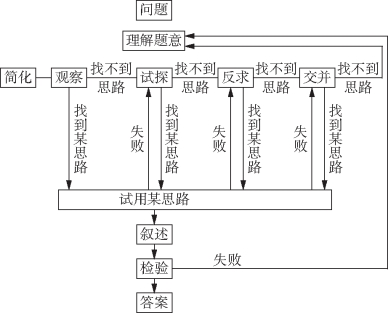
一、例题精讲
例1 在△ABC中,角A、B、C所对的边分别为a、b、c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为________.
解题策略 本题是2018年高考数学江苏卷第13题,是一道解三角形的题目,虽然仅是一道小题,却包含极其丰富的内容,要求三角形边长组成的代数式4a+c的最小值,关键是如何构建4a+c的关系式使之可以用最为常见的解题方法求最小值,这里可以调动众多的知识实现这一目标:比如可以抓住角平分线,利用面积关系求a与c的关系式代入4a+c能利用基本不等式求解;比如由三角形内角平分线的向量关系得a、c的另一关系式;比如运用解析法抓住A、D、C三点共线,kAD=kCD即得a、c的关系式;比如根据内角平分线定理借助平面几何知识求解;比如抓住△ABD、△BCD和△ABC利用正弦定理得a与c的另一个关系式,等等.更为简单的是构造图形获得妙思巧解.一道小题可以联想到与之有关联的众多的知识点和相应的解题方法,是以点带面的绝妙好题.当然在最后归结为应用基本不等式求解最值时,要注意对条件“一正、二定、三相等”进行检验,尤其是等号成立的条件.
解法一 (利用面积关系)∵S△ABC=S△ABD+S△CBD,
![]() 即
即![]()
![]()
当且仅当![]() 即
即![]() 时取等号,(4a+c)min=9.
时取等号,(4a+c)min=9.
解法二 (利用向量关系)由三角形内角平分线得向量式![]()
![]()
即![]() (定值).
(定值).
![]()
当且仅当4(a-1)=c-1,即![]() 时取等号,(4a+c)min=9.
时取等号,(4a+c)min=9.
解法三 (利用三点共线斜率相等)如图1-22所示,以B为坐标原点,BC所在直线为x轴建立平面直角坐标系,则有![]()

图1-22
∵A、D、C三点共线,则kAD=kCD,
即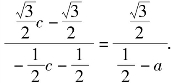
则有![]() 下同解法一.
下同解法一.
解法四 (利用内角平分线性质定理)在△BDC中,由余弦定理得![]() ,同理
,同理![]()
根据内角平分线性质定理知![]() 即
即 两边平方,并利用比例性质
两边平方,并利用比例性质![]() 整理得(a-c)(a+c-ac)=0.
整理得(a-c)(a+c-ac)=0.
当a=c时,可解得a=c=2,4a+c=10;
当a+c=ac时,![]() 下同解法一.
下同解法一.
解法五 (利用正弦定理)在△ABD与△BCD中,由正弦定理得
![]()
在△ABC中,由正弦定理得
![]()
![]() 由正弦定理得
由正弦定理得![]() 即ac=a+c,也即
即ac=a+c,也即![]() 下同解法一.
下同解法一.
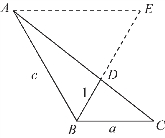
图1-23
解法六 (构造图形,利用相似三角形)如图1-23所示,作AE∥BC,交BD的延长线于点E.易得△ABE为正三角形,则AE=c,DE=c-1.
由△ADE∽△CDB,得![]() 即
即![]()
从而a+c=ac,即![]() 下同解法一.
下同解法一.
例2 已知椭圆![]() 的焦点在x轴上,A是E的左顶点,斜率为k(k<0)的直线交E于A、M两点,点N在E上,MA⊥NA.
的焦点在x轴上,A是E的左顶点,斜率为k(k<0)的直线交E于A、M两点,点N在E上,MA⊥NA.
(1)当t=4,|AM|=|AN|时,求△AMN的面积;
(2)当2|AM|=|AN|时,求k的取值范围.
解题策略 解析几何试题一般计算量大,对学生运算能力要求较高.寻求简捷、合理的解题途径显得尤为重要.因此,在解答二次曲线的综合问题时,应根据曲线的几何特征,将所求问题代数化,再结合其他知识解答.解题时,要充分利用设而不求法、弦长公式及方程根与系数的关系等知识,重视函数与方程的思想方法、数形结合的思想方法、对称思想、等价转化思想的应用.第(1)问,根据|AM|=|AN|和椭圆的对称性,求出k的值,进而可得△AMN的面积.由于直线方程AM、AN可用参数式表示,利用其几何意义可得巧妙解法.第(2)问,根据已知条件求出t和k之间的关系,利用t>3求k的取值范围.第(2)问的解答可以从不同的角度去构想,如由图像的几何特征寻求思路,如由直线的参数方程利用其几何意义求解,如由直角坐标向极坐标转化寻找巧思妙解,本题解答的自由度相当开阔,给学生提供了发挥才智的广阔平台.
本题是2016年高考数学全国卷Ⅱ理科第20题,难度属于中档,但给学生解答的知识与方法的容量特别大、特别具有典型性,在攻克压轴题的过程中紧紧抓住此类好题,以点带面,可以迅速提升你的解题能力和数学素养.
解:(1)解法一 设M(x1,y1),则由题意知y1>0.
当t=4时,E的方程为![]() 由已知及椭圆的对称性知,直线AM的倾斜角为
由已知及椭圆的对称性知,直线AM的倾斜角为![]() 因而直线AM的方程为y=x+2.
因而直线AM的方程为y=x+2.
将x=y-2代入![]() 得7y2-12y=0,解得y=0或
得7y2-12y=0,解得y=0或![]()
因此△AMN的面积![]()
解法二 当t=4时,椭圆![]() 由MA⊥AN,|AM|=|AN|,得k=1,
由MA⊥AN,|AM|=|AN|,得k=1,
∴直线AM的方程为y=x+2,则点A(-2,0),设点M(x,y),
由![]() 得7x2+16x+4=0,解得
得7x2+16x+4=0,解得![]() 即
即![]()
而△AMN为等腰直角三角形,因此△AMN的面积![]()
解法三 当t=4时,椭圆E的方程为![]() (https://www.xing528.com)
(https://www.xing528.com)
由已知及椭圆的对称性知,△AMN是等腰直角三角形,![]()
直线AM的参数方程为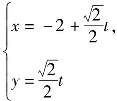 (t为参数),与
(t为参数),与![]() 联立得
联立得
![]()
解得t=0或![]() 由参数t的几何意义知
由参数t的几何意义知![]()
∴△AMN的面积![]()
(2)解法一 由题意知,![]()
将直线AM的方程![]() 代入
代入![]()
得![]()
由![]() 得
得![]()
故![]()
由题设知,直线AN的方程为![]() 故同理可得
故同理可得![]()
由2|AM|=|AN|,得![]() 即(k3-2)t=3k(2k-1). ①
即(k3-2)t=3k(2k-1). ①
当![]() 时①式不成立,因此
时①式不成立,因此![]() 等价于
等价于
![]() 即
即![]()
由此得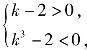 或
或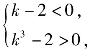 解得
解得![]()
因此k的取值范围是![]()
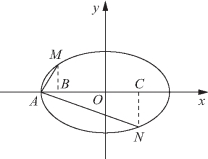
图1-24
解法二 如图1-24所示,作MB⊥x轴,垂足为B,NC⊥x轴,垂足为C.
设A、M、N的坐标分别为A(xA,yA)、M(xM,yM)、N(xN,yN).
∵AM⊥AN,∴Rt△ABM∽Rt△NCA,
![]() 有xN-xA=2yM, ①
有xN-xA=2yM, ①
即xN+2=2yM.
设直线AM的方程为![]() 由
由 得
得
![]()
当Δ>0时,由![]() 得
得![]()
![]()
又AM⊥AN,将xM中的k换成![]() 得
得![]()
代入①式得(k3-2)t=6k2-3k,易知![]()
又∵椭圆E的焦点在x轴上,得t>3,即![]()
即![]() 即(k2+1)(k-2)(k3-2)<0,解得
即(k2+1)(k-2)(k3-2)<0,解得![]() 故k的取值范围是
故k的取值范围是![]()
解法三![]() 设AM的倾斜角为
设AM的倾斜角为![]()
则直线AM的参数方程为 (m为参数);
(m为参数);
直线AN的参数方程为 (n为参数).
(n为参数).
又∵M、N在椭圆E上,则![]()
![]() 又2|AM|=|AN|,∴2|m|=|n|.
又2|AM|=|AN|,∴2|m|=|n|.
即![]() 即
即![]()
∴t(k3-2)=3k(2k-1),又![]() 又t>3,
又t>3,
![]() 即
即![]() 解得
解得![]()
故k的取值范围是![]()
解法四 ∵椭圆E的焦点在x轴上,∴t>3,原图形不变,坐标轴向左平移![]() 个单位后,椭圆E的方程为
个单位后,椭圆E的方程为![]()
以原点为极点,以x轴的正半轴为极轴建立极坐标系,则E的极坐标方程为
![]()
设点![]() 点
点![]() 点M、N在椭圆E上,则
点M、N在椭圆E上,则
![]() 则2ρ1=ρ2,
则2ρ1=ρ2,
![]() 即t(sin3θ-2cos3θ)=3sinθcosθ(2sinθ-cosθ),
即t(sin3θ-2cos3θ)=3sinθcosθ(2sinθ-cosθ),
即t(tan3θ-2)=6tan2θ-3tanθ,而tanθ=k,∴t(k3-2)=6k2-3k,又t>3,
![]() 即
即![]() 解得
解得![]()
故k的取值范围是![]()
二、发散训练
1. 已知实数a、b、c满足a+b+c=0,a2+b2+c2=1,则a的最大值是________.
2. 在平面直角坐标系xOy中,A为直线l:y=2x上在第一象限内的点,B(5,0).以AB为直径的圆C与直线l交于另一点D.若![]() 则点A的横坐标为________.
则点A的横坐标为________.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




