G·波利亚指出：“一般来说，一道题目如果可以通过将特殊数据代入某一道以前解过的一般题目中来解或者按照某一道陈旧而明显的例子依样画葫芦，而无需一丝一毫地独创，那么这道题目就是一道常规题目”“教授数学时可能需要一些常规题目，有时甚至需要许多常规题目”“但是不让学生去做其他类型的题目是不可原谅的”“寻找适用于所有类型的题目的万能规则，是一个古老的哲学梦想，而这个梦想将永远只有梦想罢了.”
显然高考数学压轴题并非是常规题目，依样画葫芦的常规解题套路根本无法解决此类难题，需要活用形式多样、丰富多彩的解题策略才能奏效.G·波利亚指出：“求解一个问题的重要方式是构造出一个解题计划的思路”“解题的成功要靠正确思路的选择，要靠从可以接近它的方向去攻克堡垒，为了辨别哪一条思路正确，哪一方向可以接近它，就要试探各种方向和各种思路.”解题的思路主线往往不易一下子抓住，需要解题者对扑朔迷离的表象进行由表及里、去伪存真的分析、加工、改造，从不同方向探索，以不同的角度审视，在广阔的范围内选择思路和策略.正确的解题思路和策略的确定非常重要，正如法国生理学家贝尔纳所言：“良好的方法使我们能够更好地发挥运用天赋的才能，而拙劣的方法则会抑制才能的发挥.”
比较常用的解决压轴题的策略有正难则反、整体处理、进退自若、归纳猜想、推理论证、类比推广、阅读迁移、构造建模等.
活用解题策略，首要任务是优化思维、展开想象、激发灵感、借石攻玉.其中相似联想非常重要，相似联想就是由问题的已知条件或结论，联想到与其相似的数学定义、定理、公式和图形等，从而把要解决的某个问题的原则和方法迁移到相似的问题上，在这个新问题的知识领域内运用最为基本的解题方法加以攻克.这样，往往可使难题化为简单的问题，生疏的问题化为熟悉的问题，从而达到正确而迅速解题的目的，而且不同的相似联想可以产生多种不同的解法，常常是别开生面，意想不到又合情合理的.
一、例题精讲
例1 函数
的最大值为________.
解题策略 本例的求解条件仅为所给出的函数解析式，分析这一解析式的特点可以产生多种联想，进而得到多种解法.
解法一 (利用三角函数的有界性)
化简得sinx-ycosx=4-3y.
由正弦函数的有界性知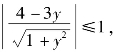
解得
故函数
的最大值为
解法二 (数形结合)观察函数
的外形结构，可以联想到斜率的表达式，即可看作定点P(3,4)与动点(cosα,sinα)连线的斜率.而动点(cosα,sinα)的轨迹是一单位圆.
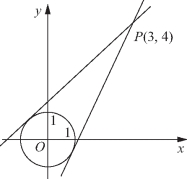
图1-14
设过点P(3,4)的直线方程为y-4=k(x-3)，即kx-y+4-3k=0.
如图1-14所示，当斜率取得最大值时，该直线是单位圆的一条切线，故原点到直线的距离为1，则
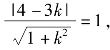即
解得
因此函数
的最大值为
解法三 (构造向量法)
整理得ycosx-sinx=3y-4.
构造向量
利用
得到
即
解得
当且仅当
即
时取等号.
故函数
的最大值为
解法四 (万能置换，判别式法)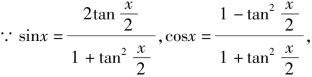
将其代入
化简得
当2y-2≠0时，由Δ≥0得到
故函数
的最大值为
解法五 (应用柯西不等式)
整理得ycosx-sinx=3y-4.
利用柯西不等式得到(3y-4)2=(ycosx-sinx)2≤(cos2x+sin2x)[y2+(-1)2].
化简得(3y-4)2≤y2+1，解得
故函数
的最大值为
例2 已知a、b、x、y均为正数，且
求证：
解题策略 本例是条件不等式的证明，如何由条件产生联想找到证法是突破此题的关键.当然，为了使条件与欲证不等式之间的联系变得明朗，可对不等式等价变形，再巧妙运用条件.
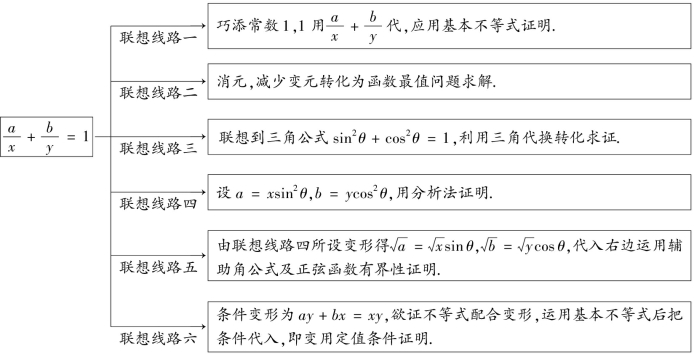
证法一 (“1”的代换)∵a、b、x、y均为正数，且
∴x+y
当且仅当
时“=”成立，即
证法二 (消元转化法)由
得
代入，有
x+y
当且仅当
即
时“=”成立，故原不等式得证.
证法三 (利用三角代换转化证明)依题设
有
x+y
即
证法四 (三角代换运用分析法证明)依题设a=xsin2θ，b=ycos2θ，有
x+y
故原不等式得证.
证法五 (三角代换运用辅助角公式及正弦函数有界性证明)
依题设可得
有
证法六 (变用定值条件证明)
由a、b、x、y均为正数，且
得
∴x-a>0，y-b>0，ay+bx=xy
∴不等式
成立.
例3 设α,β是实系数方程x2-(2a+1)x+a+2=0的虚根，并且它们的立方是实数，求a的值.
解题策略 问题所提供的条件可分解为两部分：
(1)α、β是实系数方程的虚根；
(2)α、β的立方是实数.
所求a的值就是这两个条件构成两个集的交集.
一般的解题思路是从条件(1)入手，根据“实系数方程虚根成对”定理(这是最容易联想到的)，可设α=m+ni，β=m-ni(m,n∈R)，然后再利用条件(2)求解.试设想：α3=(m+ni)3∈R且β3=(m-ni)3∈R，解出m、n的值，再运用韦达定理求a的值，计算量对于这样一道基础题实在太大.让我们注意观察问题的关系结构，即可发现条件(2)显示着问题的特征，在本题中处于主导地位，如果抓住这个特征，联想与之相关的知识，可得以下几条线路.
本例中的α、β是实系数方程x2-(2a+1)x+a+2=0的虚根，并非是三次单位原根ω，故联想线路一不必进一步考虑，联想线路二正如上面的分析，计算量太大，就此打住，我们需要的是一条简捷的线路，进一步审视可以发现若α3∈R,则
由此出发进一步产生联想：
解：∵α、β是实系数方程x2-(2a+1)x+a+2=0的虚根，
可得
(α-β)[(α+β)2-αβ]=0,∵α≠β,∴(α+β)2-αβ=0.
∴运用韦达定理得(2a+1)2-(a+2)=0，解得
或a=-1，均满足Δ<0，故所求a的值为
或-1.
例4 (2016年高考上海卷理科第22题)已知a∈R，函数
(1)当a=5时，解不等式f(x)>0;(www.xing528.com)
(2)若关于x的方程f(x)-log2[(a-4)x+2a-5]=0的解集中恰好有一个元素，求a的取值范围；
(3)设a>0，若对任意
函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1，求a的取值范围.
解题策略 本例以对数函数为载体，考点一：解对数不等式，方法是“抓住单调性，不忘定义域”，照常规解法走就是！考点二：已知含参数对数方程恰有一解，求参数a的取值范围，在“脱去”对数符号后转化为关于x的代数方程恰有唯一解，即
有唯一解.
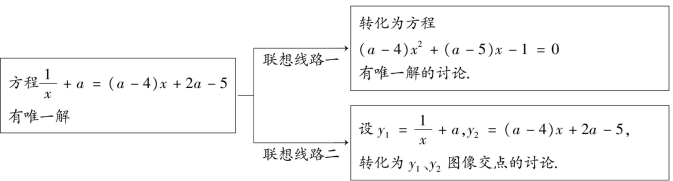
对于联想线路一，对二次项系数是否为零是一个讨论点，当二次项系数不为零时恰有一解，则另一解应当不符合定义域而被排除.对于线路二，运用数形结合肯定是妙思巧解，符合条件的仅有一个交点必须在定义域范围内，函数f(x)在变动区间内的最大值与最小值之差不超过1，由复合函数的单调性知f(x)在区间[t,t+1]上单调递减，有
恒成立，转化为求
的最大值.
此类含参数不等式问题，研究相应函数的性态很重要，每一条联想线路产生各自独特的解题方法，妙不可言，精彩!
解：(1)
解得
或x>0.
(2)解法一 (转化为方程有唯一解的讨论)
化简得(a-4)x2+(a-5)x-1=0，即(x+1)[(a-4)x-1]=0.
当a=3或a=4时，都只有唯一解x=-1，且都满足
当a≠3且a≠4时，有两解x=-1或
若x=-1为方程的解，则
即a>1；
若
为方程的解，则
即a>2.
∴要满足恰有一个解，则1<a≤2.
综上，a的取值范围为(1,2]∪{3,4}.
解法二 (数形结合法)
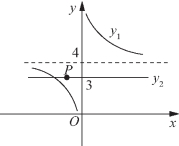
图1-15
令
直线y2恒过点P(-2,3),则条件转化为当y1、y2的图像在x轴上方有且仅有一个交点.
1当a=4时，
显然满足题意，见图1-15；
当a≠4时，由
得(a-4)x2+(a-5)x-1=0.
其中
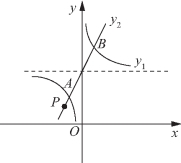
图1-16
2当a>4时，如图1-16所示，
∵x=-2时，
∴y1、y2必有两个交点A、B，且均位于x轴上方，不合条件.
3当a<4时，
由图像可知直线与曲线的左半支有两个交点或一个交点.
(a-4)x2+(a-5)x-1=0，解得
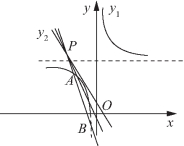
图1-17
如图1-17所示，x1、x2的值为A、B两点的横坐标.
故A、B重合(图中相切时)或一点在x轴上方，另一点在x轴下方.
或
从而a=3或1<a≤2.
综上所述，a的取值范围是[1,2]∪{3,4}.
(3)f(x)在区间[t,t+1]上单调递减，依题意f(t)-f(t+1)≤1,
即
参变分离得
恒成立.
设
则a≥g(t)max，问题转化为求
的最大值.
解法一 (转化为“耐克函数”求最值)
设
设m=1-t，则
有
若m=0，则h(m)=0,
若m≠0，则
在
上单调递减,
∴a的取值范围是
解法二 (转化为含参数一元二次不等式恒成立问题，运用函数与方程的思想方法)
由
得at2+(a+1)t-1≥0.
记k(t)=at2+(a+1)t-1，其对称轴
∴k(t)在
上是增函数，只要
解得
∴a的取值范围是
解法三 (利用导数求g(t)的最大值)
设
则
由g′(t)=0，得
∴g(t)在区间
上单调递减，则
∴a的取值范围是
解法四 (数形结合)
由f(t)-f(t+1)≤1得
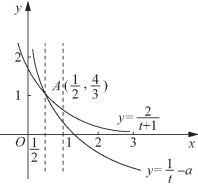
图1-18
化简得
对任意
不等式恒成立.
只要当
时，函数
的图像在函数
的图像下方.由于两个函数在
上都是减函数，如图1-18所示，可知
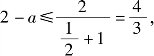解得
显然当
时，两函数图像相交于点
∴a的取值范围是
二、发散训练
1. 设椭圆中心在坐标原点，A(2,0)，B(0,1)是它的两个顶点，直线y=kx(k>0)与AB相交于点D，与椭圆相交于E、F两点，求四边形AEBF面积的最大值.
2. 已知数列{an}满足：
且
(1)求数列{an}的通项公式；
(2)求证：对于一切正整数n，不等式a1·a2·…·an<2·n!恒成立.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
